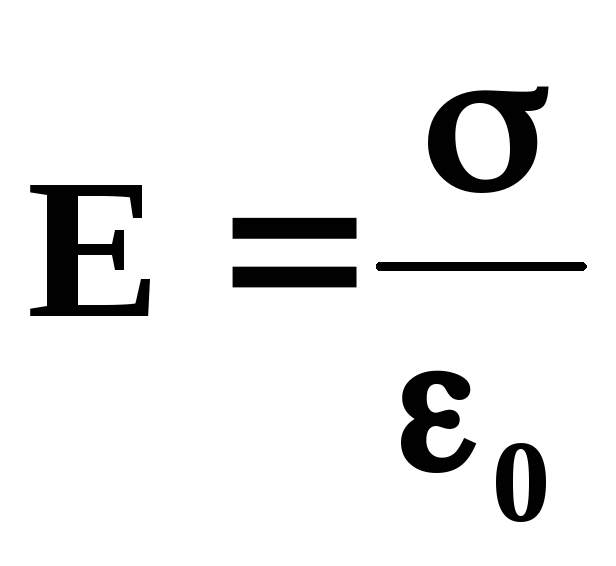Введение
Расчет и анализ электрических потенциалов, возбуждаемых токовыми источниками
в проводящих телах, представляют интерес в ряде практических задач, например в
электрогеоразведке, электрокардиографии, электроэнцефалографии и других. Использование
методики расчета электрических потенциалов актуально при решении обратных
задач, связанных с неинвазивным определением (реконструкцией) координат и
ориентации токовых источников по электрическим потенциалам, измеренным на
поверхности проводящих тел. Известны численные методы решения уравнений теории
поля (уравнения Пуассона и Лапласа) − это метод конечных элементов и
метод граничных элементов (МКЭ и МГЭ, соответственно). Однако, при достаточно
сложной форме поверхности проводящих тел и при учете внутренних неоднородностей
в проводящих телах, вычислительная трудоемкость МКЭ и МГЭ становится препятствием
на пути решения обратных задач, в которых прямой расчет потенциалов проводится
многократно. В силу вышесказанного актуальным является анализ моделей
проводящих тел, которые, с одной стороны отражают наиболее существенные свойства
таких тел, и, с другой стороны, допускают аналитические методы расчета
электрических потенциалов.
В работах [] рассмотрены методы расчета потенциалов для случая аппроксимации
поверхности проводящего тела сферой [] или сфероидом вращения [].
Однако, применительно, например, к задачам электрокардиографии более
реалистичной является аппроксимация поверхности торса цилиндром конечной длины.
Имеется несколько работ, посвященных расчетам потенциалов, возбуждаемых
точечным токовым диполем в проводящем круговом цилиндре [], в работе [] рассмотрен
случай эллиптического цилиндра.
Целью настоящей статьи является вычислительная
реализация подхода, предложенного в работе [], проверка сходимости
используемых рядов функций Матье, сопоставление получаемых распределений
поверхностных потенциалов с распределениями, полученными численными методами
при различных ориентациях дипольного источника внутри эллиптического цилиндра
конечной длины. Необходимо также убедиться в согласованности методов расчета потенциалов
в круговом цилиндре и в эллиптическом цилиндре с малым эксцентриситетом.
Похожие:
| Электростатика. Потенциал. Работа заряд под действием сил электростатического поля перемещается из точки 1 в точку2, при этом поле совершает работу 3 Дж. Чему р | Точечный заряд +q находится в центре сферической поверхности. Если добавить заряд +q за пределами сферы, то поток вектора напряженности электростатического поля через поверхность сферы… | ||
| Самостоятельная работа ориентировочный вариант (Напряженность эп. Работа. Потенциал.) По какой формуле определяется напряженность электрического поля? Выберите и запишите правильный ответ: 1)E = F/q; 2)E = Fq; 3)E = kq; 4)E = k/q | 1. Закон Кулона. Закон сохранения заряда. Принцип суперпозицииЭлектростатическое поле (напряженность электростатического поля, поле точечного покоящегося электрического заряда, потенциальность… | ||
| Энергия заряженного проводника и конденсатора. Энергия электростатического поля. Объемная плотность энергии | Чему должно быть равно отношение длины катушки к ее диаметру, чтобы напряженность магнитного поля в центре катушки можно было найти по формуле для напряженности | ||
| Ионизация атомов и молекул и рекомбинация ионов. Ударная ионизация. Работа и потенциал ионизации. Электронные лавины. Газовый разряд. Несамостоятельный и самостоятельный газовые разряды. Виды разрядов | Контрольная работа №1 по теме «Строение атома. Химическая связь» Инструкция для учащихся | ||
| Контрольная работа «Электромагнитное поле»Какова индукция магнитного поля, в котором на проводник с длиной активной части 5см действует сила 50 мН? Сила тока в проводнике… | Влияние стратегии регионального развития на приоритеты управления трудовым потенциалом |
Влияние электрического поля на различные материалы
Электрическое поле оказывает различные эффекты на различные материалы, в зависимости от их свойств и химической структуры.
1. Изолирующие материалы (например, стекло, керамика, резина) обладают высокой сопротивляемостью электрическому току и не проводят заряды. В электрическом поле они создают пространственное смещение зарядов, но сами остаются электрически нейтральными.
2. Проводящие материалы (например, металлы) хорошо проводят электрический ток и в электрическом поле заряды свободно перемещаются. Электрическое поле внутри проводника равно нулю, так как заряды находятся в состоянии равновесия.
3. Поляризуемые материалы (например, диэлектрики) реагируют на электрическое поле путем поляризации, то есть смещения электронных облаков атомов или молекул. В результате поляризации, внутри диэлектрика возникает индуцированный дипольный момент, который влияет на величину и направление электрического поля.
4. Магнитные материалы (например, железо, никель, кобальт) обладают способностью взаимодействовать с магнитным полем. В электрическом поле они могут изменять свою магнитную структуру, что приводит к возникновению магнитных полюсов и магнитных сил.
5. Пьезоэлектрические материалы (например, кварц, резонаторы) изменяют свою форму или размеры под влиянием электрического поля. Это свойство позволяет использовать их для создания ультразвуковых устройств и генераторов.
Все эти эффекты демонстрируют, как важно учитывать свойства материалов при анализе и решении задач, связанных с электрическим полем
3.3. Потенциальная энергия и потенциал электростатического поля
q‘qqconstq‘q‘qrпотенциаломпотенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.q1q2qnr1r2rnсилами поляпотенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки поля в бесконечность, или работе, которую надо совершить против сил электрического поля для того, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля3.4. Диполь в электростатическом полеЭлектрическим диполемlр=qlдипольным моментомот отрицательного заряда к положительномуqq. qqqE, р .dαWconst=0const=0-рЕ)рЕf1 f2ххЕ , ff= –.
Исходная задача
Рассматривается проводящий прямой эллиптический цилиндр высотой и полуосями эллипса соответственно
большой и малой − и (рис. 1). Проводимость внутренней
среды известна и равна .
Пусть и −радиус-векторы точки наблюдения и точки источника,
соответственно.
|
Рис. 1. Проводящий эллиптический цилиндр конечной длины. |
Уравнение Пуассона для потенциала в данном
случае имеет вид:
|
(1) |
где − вектор дипольного
момента точечного токового диполя; дифференцирование в правой части поводится
по координатам источника. Проводящий цилиндр окружен воздухом с нулевой
проводимостью, поэтому на поверхности цилиндра потенциал удовлетворяет
граничному условию электрической изоляции:
|
(2), (3) |
где − радиус-вектор точек,
принадлежащих боковой поверхности цилиндра.
Решение исходной задачи.Решение
уравнения Пуассона (1) может быть получено с помощью функции Грина , удовлетворяющей граничным условиям (2),
(3) и являющейся, по сути, полем монопольного точечного источника []:
|
(4) |
Следуя , функцию Грина можно представить в виде
|
(5) |
где собственные функции удовлетворяют
граничным условиям (2), (3) и являются решениями уравнения Штурма-Лиувилля []
|
(6) |
со спектром собственных значений ,
причем суммирование в (5) проводится по всем собственным значениям, кроме . Собственные функции должны образовывать базис, нормированный
по объему цилиндра:
|
(7) |
Поскольку граничное условие (2) должно выполняться на поверхности
эллиптического цилиндра, то разделение переменных в (6) проводится в эллиптических
координатах:
|
(8) |
где −
расстояние между фокусами эллиптических оснований цилиндра, угловая координата , радиальная эллиптическая координата на поверхности цилиндра , где .
Следуя работе [], решение уравнения Штурма-Лиувилля (6) в координатах
методом разделения переменных приводит к
собственным функциям
|
(9) |
где и являются
соответственно периодическими (угловыми) и модифицированными
(радиальными) функциями Матье, т.е. решениями уравнений:
|
(10) |
|
|
(11) |
для одинаковых значений и . При подстановке (9) в (6), учитывая
граничное условие (3) на основаниях цилиндра, получается характеристическое
уравнение
|
(12) |
Характеристические значения и определяются граничным условием ()
для радиальных функций Матье и условием периодичности по углу для угловых
функций Матье. Существенно, что частные случаи (отсутствие
вариаций в поперечной плоскости ) и (отсутствие вариаций вдоль оси цилиндра)
приводят к частным выражениям для коэффициентов в (9)
в связи с условием нормировки ().
В работе [] для удобства определения
коэффициентов предложено
использовать дополнительное нормирующее условие на функции Матье:
|
|
(13) |
При этом в [] получены следующие выражения для потенциалов, создаваемых
токовыми диполями трёх базовых ориентаций:
|
|
(14) |
для -ориентированного диполя ();
|
|
(15) |
для -ориентированного диполя ();
|
|
(16) |
для -ориентированного диполя (). Здесь и ; , множитель
в () принят для удобства за единицу.
Формулы (14)-(16) записаны при , потенциал в случае получается в результате замен и на и , а
также на . Здесь
− площадь оснований цилиндров, а − множитель, используемый при преобразовании
базисных векторов между декартовой и эллиптической системой координат.
В общем случае, когда присутствуют все компоненты вектора дипольного
момента, потенциал определяется на основе формул (14)-(16) по принципу суперпозиции:
![]() .
.
3.1. Работа сил электростатического поля
qq‘r1r2q‘qпотенциальнымqi Аq‘характерным для электростатического поля является то, что циркуляция вектора напряженности по любому замкнутому контуру равна нулю.3.2. Теорема о циркуляции вектора напряженности электростатического поляq (3)или (4) потенциальнымЛюбое электростатическое поле является потенциальным.
- Линии электростатического поля не могут быть замкнутыми. В самом деле, если это не так, и какая-то линия – замкнута, то, взяв циркуляцию вдоль этой линии, мы сразу же придем к противоречию с теоремой о циркуляции вектора : . А в данном случае направление интегрирования в одну сторону, поэтому циркуляция вектора не равна нулю.
- Электростатическое поле не вихревое. В ряде случаев для решения задачи о нахождении поля по известному неоднородному распределению зарядов с плотностью , нужны уравнения, содержащие характеристики поля в данной точке пространства или в ее малой окрестности (такое как, например, теорема Остроградского- Гаусса в дифференциальной форме). Получим такое уравнение, отражающее потенциальный характер электростатического поля.
Lэлектростатическое поле не вихревое, если .
Выполнение
1.Для заданной системы двух параллельных цилиндров,
имею- щих равные заряды противоположного знака (q1 = — q2 ) определим :
a)емкость ;
b)напряжение.
Считаем цилиндры бесконечно длинными, а поле,
создаваемое ими – плоскопараллельным.
Заменим
цилиндры заряженными нитями с линейными зарядами :
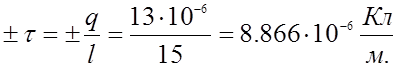 |
потенциала.
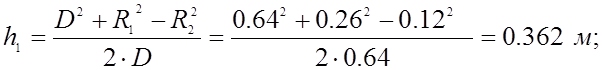 |
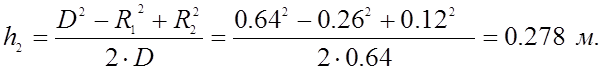 |
Определим
расстояние от плоскости нулевого потенциала до
мнимых
заряженных осей.
Определим
напряжение между цилиндрами, как разность потен-
циалов
между точками A и B.
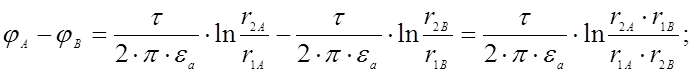
где
Откуда
получаем, что
Емкость
найдем из выражения :
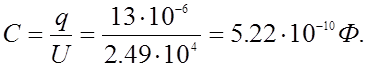 |
2.Построим графическую картину электростатического поля
, соблюдая следующие требования :
a)разность
потенциалов между двумя любыми соседними линиями
равного
потенциала должна быть одна и та же ;
b)поток вектора
напряженности электростатического поля во всех
силовых
трубках должен быть одинаков ;
с)при
построении картины поля на каждой линии равного потенциа-
ла
указать значение потенциала ; на силовых линиях должно быть
указано
их направление и ограниченное данной линией значение по-
тока
напряженности поля, отсчитываемое от некоторой фиксирован- ной линии , принятой
за начальную.
Построим эквипотенциальные
линии.
Линии
равного потенциала есть окружности сцентрами, лежащи-ми на линии, соединяющей оси цилиндров.
Радисы
находим из выражения:
Что бы разность потенциалов между соседними линиями
была
постоянной,
необходимо, что бы выполнялось следующее условие:
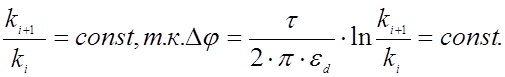 |
Примем
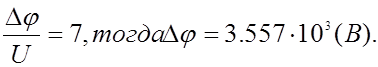 |
Найдем коэффициент геометрической прогрессии.
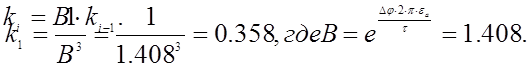 |
тогда
плучаем, что эквипотенциальные линии будут иметь окружности
радиусами
R с координатами (x;0).
|
k |
j,В |
X,м |
R,м |
|
|
1 |
0.358 |
-10920.1 |
0.3248 |
0.206 |
|
2 |
0.504 |
-7283.9 |
0.4224 |
0.3396 |
|
3 |
0.71 |
-3640.91 |
0.7613 |
0.7186 |
|
4 |
0.999 |
-10.6 |
353.12 |
353.12 |
|
5 |
1.407 |
3629.96 |
-0.7642 |
0.7217 |
|
6 |
1.981 |
7267.17 |
-0.4231 |
0.3404 |
|
7 |
2.789 |
10903.7 |
-0.3254 |
0.2067 |
Построим
силовые линии
Силовые
линии поля двух параллельных заряженных нитей пред-
ставляет
собой окружности с координатами центров :
угол, под которым расстояние между нитями видно
из любой точки
линии.
Так
как
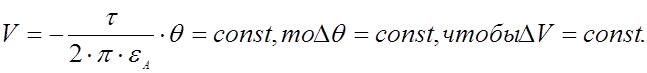
Примем
приращение угла равное:
Тогда
получим
|
q,град |
Y,м |
V,В |
|
|
1 |
15 |
0.938 |
-2720.23 |
|
2 |
30 |
0.435 |
-5440.46 |
|
3 |
45 |
0.251 |
-8160.7 |
|
4 |
60 |
0.145 |
-10880.94 |
|
5 |
75 |
0.067 |
-13601.17 |
|
6 |
90 |
-16321.41 |
|
|
7 |
105 |
-0.067 |
-19041.64 |
|
8 |
120 |
-0.145 |
-21761.87 |
|
9 |
135 |
-0.251 |
-24482.1 |
|
10 |
150 |
-0.435 |
-27202.34 |
|
11 |
165 |
-0.938 |
-29922.58 |
При
построении картины поля необходимо учитывать, что внутри цилиндров поле отсутсвует
, и следовательно там не сущест-
вует
эквипотенциальных и силовых линий.
3. Вычертим
и представим в виде графиков изменение потенциала и
напряженности электростатического поля на линии,
соединяющей
наиболее близкие точки цилиндров, и распределение
плотности заряда
на поверхности цилиндра меньшего радиуса.
Изменение потенциала электростатического поля на
линии, соединяющей наиболее близкие точки цилиндров.
Потенциал в некоторой точке, удаленной на
расстояние r1 и r1
от
электрических осей цилиндров будет равен:
Примем за начало координат – левую положительную электричес- кую ось t.Тогда координата x будет изменяться от точки А до В.
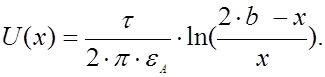 |
Тогда
получим график функции
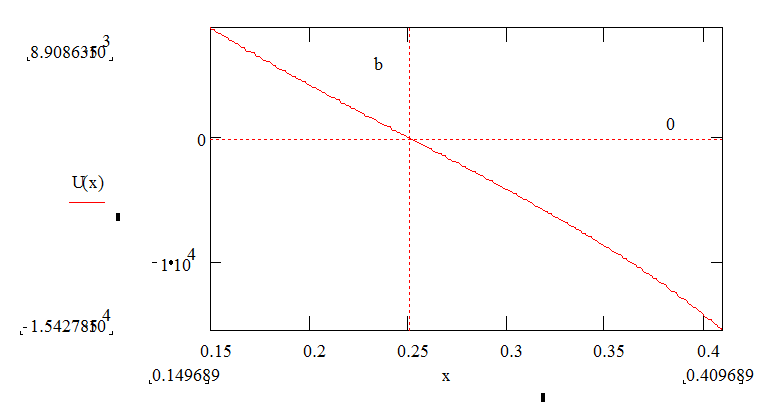 |
Изменение напряженности электростатического поля
на линии, соединяющей наиболее близкие точки цилиндров.
Это изменение находим из выражения:
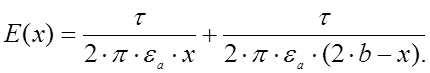 |
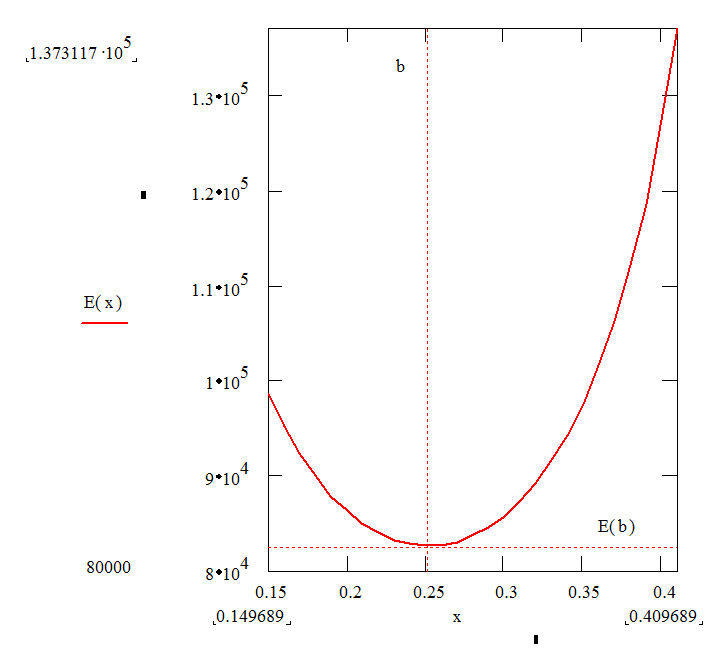
Из этого имеем график функции:
меньшего радиуса.
Исходя из граничных условий на поверхности раздела проводника
и
диэлектрика имеем, что
где u — плотность
электрического заряда на поверхности цилиндра.
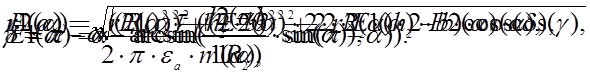
Получим график
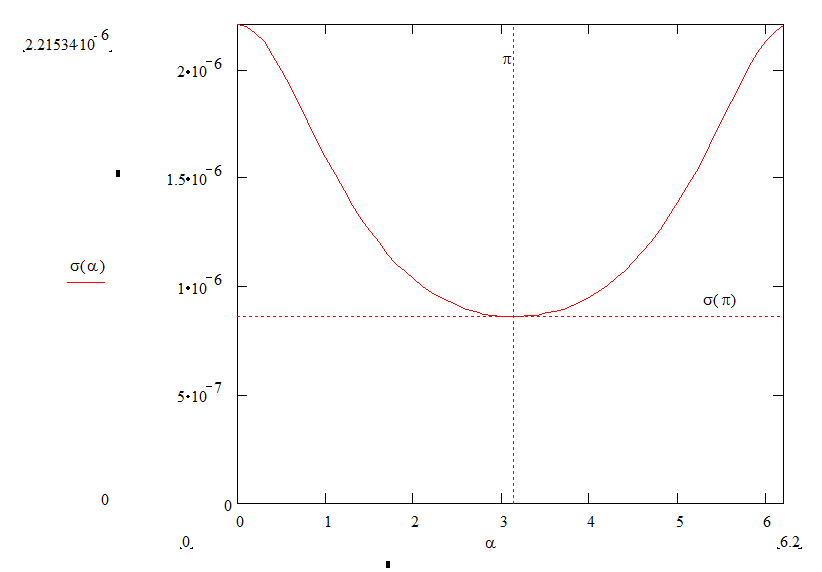
Проводники в электрическом поле.
Проводниками
называют тела, которые хорошо проводят
электрический ток, в которых есть
свободные электрические заряды, способные
перемещаться по всему объему проводника.
Условия
равновесия зарядов на проводнике:

|
|
Найдем величинуE
Отсюда:
|
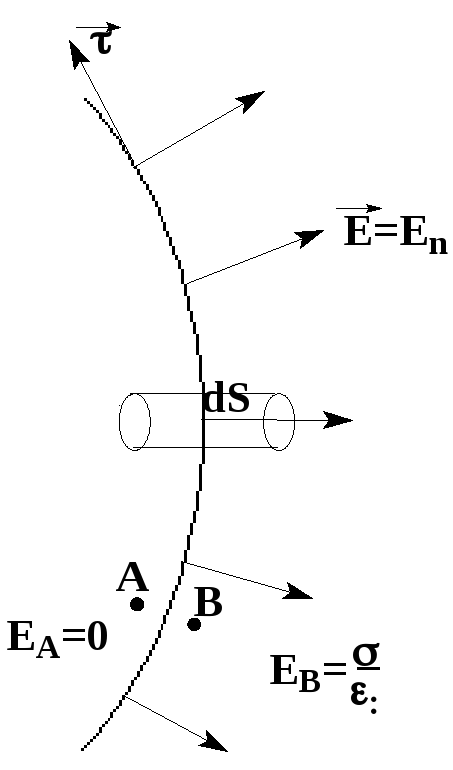
Поскольку внутри
проводника E=0,
а в непосредственной близости от
поверхности
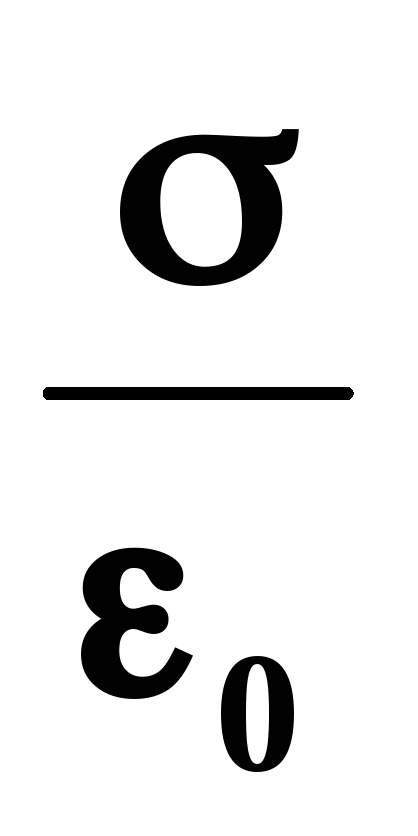

Среднее значение
напряженности поля на поверхности
проводника получается равным:
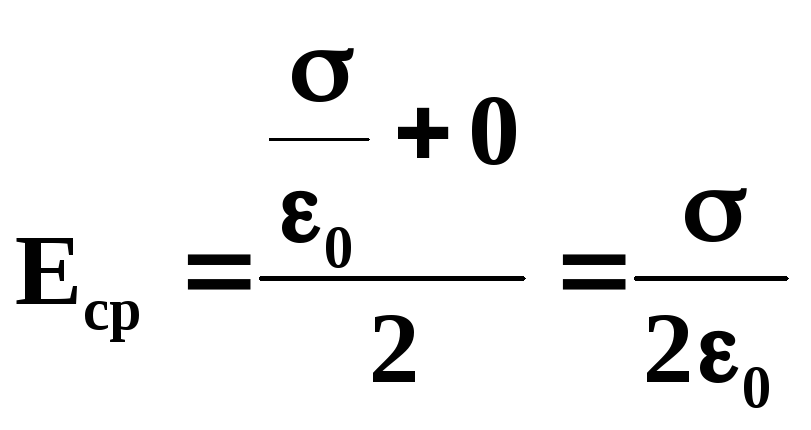
Сила, с которой
поле проводника действует на заряд,
расположенный на его поверхности dS,
равна:
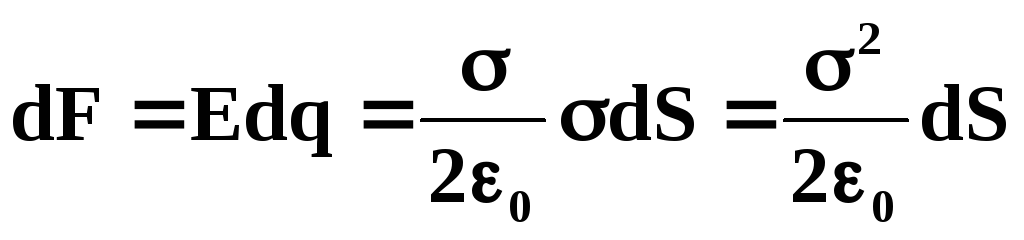
Давление, испытываемое
поверхностью проводника и обусловленное
избыточными зарядами на его поверхности,
равно:
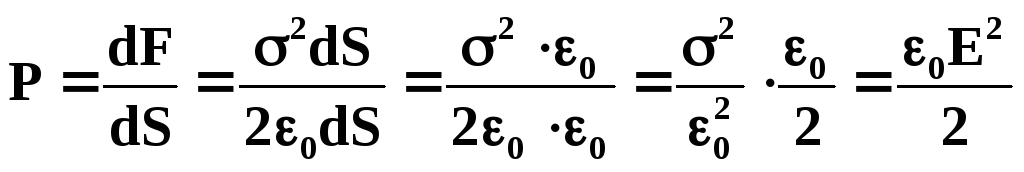
При помещении
незаряженного проводника в электрическое
поле имеющиеся на нем заряды приходят
в движение – на противоположных
поверхностях возникают избыточные
электрические заряды противоположных
знаков.
Возникающие на
поверхности заряды создают свое поле,
которое в точности равно внешнему, но
противоположно по направлению – внутри
проводника (в полости) поле отсутствует.
Перераспределение
зарядов в проводнике под действием
внешнего поля происходит до тех пор,
пока силовые линии не окажутся
перпендикулярными поверхности проводника.
Равенство нулю
напряженности поля в полости проводника
используют для реализации электрической
защиты, причем оказалось, что электрическая
защита получается достаточно хорошей
не только в случае сплошной металлической
оболочки, но и в случае использования
мелкой металлической сетки.
Соединение
проводником какого-либо тела с землей
называют заземлением. При заземлении
заряженных проводников, в том числе и
тела человека, они теряют заряд и их
потенциал будет равен потенциалу земли.
Заземление корпусов приборов и аппаратов
способствует их безопасной эксплуатации,
т.к. исключает возможность для персонала
оказаться под напряжением корпуса
аппарата и земли.
Рассмотрим
несколько примеров расчёта электростатических
полей с помощью теоремы Гаусса.
Потенциал. Разность потенциалов. ЗАДАЧИ с решениями
Формулы, используемые на уроках «Решение задач на тему: Работа перемещения заряда в электрическом поле. Потенциал. Разность потенциалов» для подготовки к ЕГЭ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Металлический шар диаметром d заряжен с поверхностной плотностью зарядов σ. Найти потенциал φ этого шара, если он окружен заземленной проводящей сферой, имеющей общий с шаром центр. Диаметр сферы D. Среда — воздух.
Задача № 2.
Потенциал заряженного шара φ1 = 300 В. Чему равен потенциал φ2 электрического поля этого шара в точке, отстоящей на расстоянии l = 50 см от его поверхности, если радиус шара R = 25 см?
Задача № 3.
Определить потенциал φ точки поля, находящейся на расстоянии а = 9 см от поверхности заряженного шара радиусом R = 1 см, если поверхностная плотность зарядов на шаре σ = 1 • 10–11 Кл/см2. Среда — воздух.
Задача № 4.
В точке 1 поля точечного заряда-источника потенциал φ1 = 40 В, а в точке 2 φ2 = 10 В. Найти потенциал φ в точке М, лежащей посередине между точками 1 и 2 (рис. 3-6).
Задача № 5.
В трех вершинах квадрата со стороной а = 20 см находятся заряды q1 = 1 • 10–8 Кл, q2 = 2 • 10–8 Кл и q3 = 2 • 10–8 Кл (рис. 3-7). Определить потенциал φ электрического поля, созданного этими зарядами в четвертой вершине.
Задача № 6.
Четыре одинаковых точечных заряда q расположены на одной прямой на расстоянии r друг от друга. Какую работу А надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.
Задача № 7.
Два одинаково заряженных шарика диаметрами d = 0,5 см каждый расположены на расстоянии l = 2 см между их поверхностями (рис. 3-14). До какого потенциала φ они заряжены, если сила их отталкивания друг от друга F = 2 мкН? Среда — воздух.
Задача № 8.
В однородном электрическом поле напряженностью Е = 2 кВ/см переместили заряд q = –20 нКл в направлении силовой линии поля на расстояние d = 10 см. Найти работу поля А, изменение потенциальной энергии поля ΔWп и напряжение (разность потенциалов) U между начальной и конечной точками перемещения.
Задача № 9.
Между двумя горизонтальными плоскостями, заряженными разноименно и расположенными на расстоянии d = 5 мм друг от друга, находится в равновесии капелька масла массой 20 нг (нанограмм) (рис. 3-10). Найти число избыточных электронов N на этой капельке. Среда — воздух. Разность потенциалов между плоскостями U = 2 кВ.
Задача № 10.
На пластине М поддерживается потенциал φ1 = +80 В, а на пластине N – φ2 = –80 В (рис. 3-11, а). Расстояние между пластинами d = 10 см. На расстоянии d1 = 4 см от пластины М помещают заземленную пластину Р (рис. 3-11, б). Найти изменение напряженности ΔЕ1 поля на участке МР и изменение напряженности поля ΔЕ2 на участке PN при этом. Построить графики зависимостей напряженностей Е = Е(х) и потенциала φ = φ(х) от расстояния между точками поля и пластинами.
Это конспект по теме «Потенциал. Разность потенциалов. ЗАДАЧИ с решениями». Выберите дальнейшие действия:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Влияние напряжения электрического поля на окружающую среду
Напряжение электрического поля имеет значительное влияние на окружающую среду, влияя на различные аспекты нашей жизни. Оно оказывает воздействие на различные материалы и объекты, в том числе на живые организмы.
Одним из наиболее заметных проявлений воздействия напряжения электрического поля является электрический разряд. При достаточно высоком напряжении электрического поля может возникнуть разряд между проводящими объектами, сопровождающийся яркой вспышкой света и сильным шумом. Это явление может быть опасным для человека и окружающей среды.
Кроме того, напряжение электрического поля может повлиять на электрические и электронные устройства, особенно если они не защищены соответствующими средствами. Высокое напряжение электрического поля может вызвать сбои и повреждения в электронике, что может привести к серьезным последствиям.
Еще одним важным аспектом воздействия напряжения электрического поля на окружающую среду является его взаимодействие с живыми организмами. Высокие уровни напряжения могут оказывать вредное воздействие на нервную систему живых существ, вызывать электрофобные реакции и даже приводить к смертельным исходам. Также напряжение электрического поля может изменять активность клеток и тканей, повлиять на метаболические процессы и вызвать другие патологические изменения.
Изучение влияния напряжения электрического поля на окружающую среду является важной задачей, которая позволяет выявить потенциальные опасности и разработать соответствующие меры предосторожности. Таким образом, необходимо учитывать воздействие электрического поля при проектировании электроустановок и принимать меры для обеспечения безопасности человека и окружающей среды


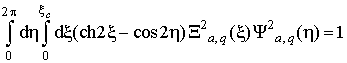
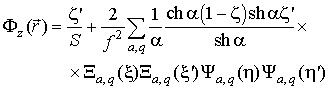
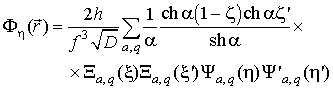
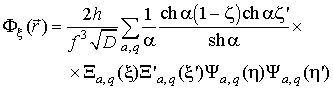










 .
.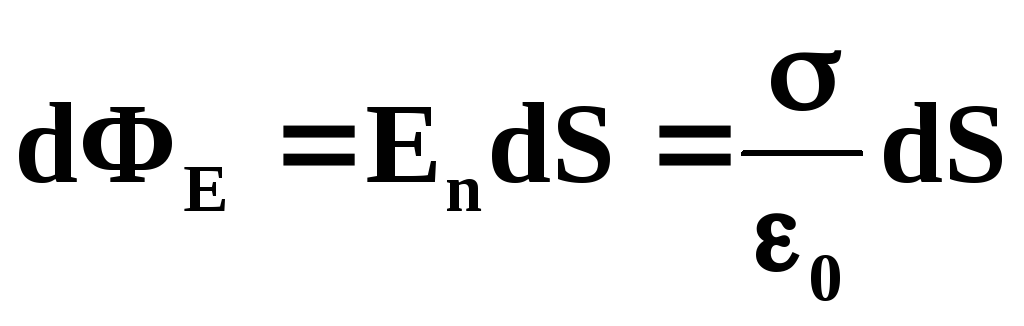 ,
,