Гдз физика 7 класс учебник, перышкин. дрофа

Как измерить длину. Погрешности измерений

На практике измерить длину отрезка достаточно просто:

• Приложить линейку к отрезку.
• Совместить ноль с началом отрезка.
• Определить число, соответствующее концу отрезка.
• Записать результат измерения.    

В приведенном примере длина отрезка 9,9 см. Как точен этот результат? Он точен до 1 мм, так как на линейке нет меньших делений. Не надо путать значения слов «штрих» и «деление».

(Источник)

Численное значение самого маленького деления шкалы прибора называется ценой деления.

Чтобы определить цену деления прибора (например, линейки), нужно взять любые два рядом стоящие числа и их разность поделить на число делений между ними (т.е. промежутков между штрихами).

Цена деления линейки = (7 см – 6 см)/10 = 0,1 см = 1 мм.

 

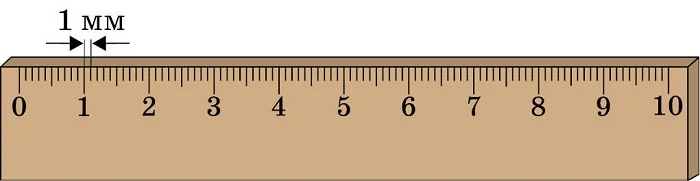
И чтобы начать измерение, прежде всего надо найти цену деления прибора, который используется в данном случае. Любое измерение дает некоторую погрешность, зависящую от качества прибора. Поэтому ее называют погрешностью прибора.

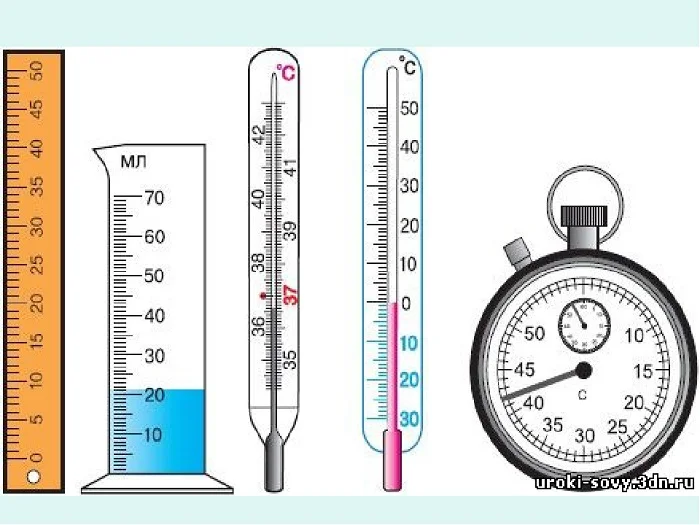Шкалы различных приборов. (Источник)

Известно, что измерить какую-то величину – это значит сравнить ее с эталоном. На практике пользуются не эталонами, а специальными приборами (линейка, часы и др.), которые являются копиями с эталонов, изготовленными с определенной точностью. Абсолютно точных измерений не бывает. При использовании линейки допускается погрешность отсчета, которая равна половине цены деления прибора (0,5 мм). Сумма погрешностей прибора и отсчета называется абсолютной погрешностью. Она равна цене деления прибора.

Абсолютная погрешность обозначается значком Δ (дельта). Для школьной линейки Δ = 1 мм. Δ показывает, на сколько совершается ошибка при использовании того или иного прибора. Для более точных измерений используется штангенциркуль. В устройстве штангенциркуля заложено две шкалы, неподвижная (Δ = 1 мм) и подвижная (Δ = 0,1 мм).

                               Штангенциркуль.                                           Микрометр.  

А вот при помощи микрометра, где используется не перемещение шкалы, а ее вращение измерить длину можно с точностью до 0,01 мм. Но это еще не предел. В очень точных технологиях определяются размеры с точностью до 10-7м, в научных разработках точность возрастает во много раз. Но для этого нужны сверхточные приборы.

На практике, используя приборы, необходимо учитывать качество измерения. Величина, которая помогает это учесть, называется относительной погрешностью σ (сигма) и выражается в процентах.

σ = Δ / L ( L – измеренная величина)

     Пример: Требуется замерить длину L отрезка различными приборами: 1) линейкой, 2) штангенциркулем и 3) микрометром. Длина отрезка получилась 55 мм. Какова относительная погрешность этих трех измерений?

 1) Δ₁ = 1 мм, L = 55 ± 1 мм, σ₁ = 1 мм / 55 мм ≈ 0,018 (1,8%);

   2) Δ₂ = 0,1 мм, L = 55 ± 0,1 мм, σ₂ = 0,1 мм / 55мм ≈ 0,0018 (0,18);

   3) Δ₃ = 0,01 мм, L = 55 ± 0,01 мм, σ₃ = 0,01 мм / 55мм ≈ 0,00018 (0,018%).

Как видно, более точный прибор (микрометр) дает меньший процент ошибки.

Для каждого конкретного измерения в технике, практической деятельности человека и в науке существует своя точность измерения, в соответствии с которой применяются измерительные приборы.

Виды измерительных цилиндров и их применение

Существует несколько видов измерительных цилиндров, каждый из которых обладает своими особенностями и применением.

Стеклянный цилиндр — один из наиболее распространенных и простых в использовании типов измерительных цилиндров. Он выполнен из прозрачного стекла и имеет маркировку, позволяющую наглядно определить уровень жидкости. Стеклянный цилиндр широко применяется в лабораторных условиях для измерения объема жидкости или газа, а также для точного дозирования реактивов.

Пластмассовый цилиндр – это бюджетный и более прочный вариант измерительного цилиндра. Он обычно делается из прозрачной или полупрозрачной пластмассы и также имеет маркировку для точного измерения. Пластмассовые цилиндры могут использоваться как в лаборатории, так и на производстве, где требуется большее количество измерений.

Металлический цилиндр применяется там, где требуется большая точность и измерения производятся в условиях повышенной температуры или давления. Он обычно изготавливается из нержавеющей стали и имеет специальные маркировки для измерения. Металлические цилиндры часто используются в промышленности и экспериментах.

Цилиндр Мохра – это специальный тип измерительного цилиндра, который используется для измерения объема жидкости посредством определения уровня поверхности воды в цилиндре с помощью шкалы. Цилиндр Мохра широко применяется в школьных и учебных лабораториях.

Конический цилиндр – это форма измерительного цилиндра, которая позволяет измерять объем жидкости с большей точностью. Он имеет коническую форму с узким основанием и более широким верхним диаметром. Конические цилиндры применяются в лабораторных условиях для измерения небольших объемов жидкости с высокой точностью.

В зависимости от требований и условий эксплуатации можно выбрать наиболее подходящий тип измерительного цилиндра. Каждый из видов цилиндров обладает своими преимуществами и предназначен для определенной области применения.

Измерение объема. Мензурка

При измерении пространства нужно перейти к трем измерениям, так как представление о пространстве дает объем. Известны формулы объемов параллелепипеда, куба, шара, цилиндра.

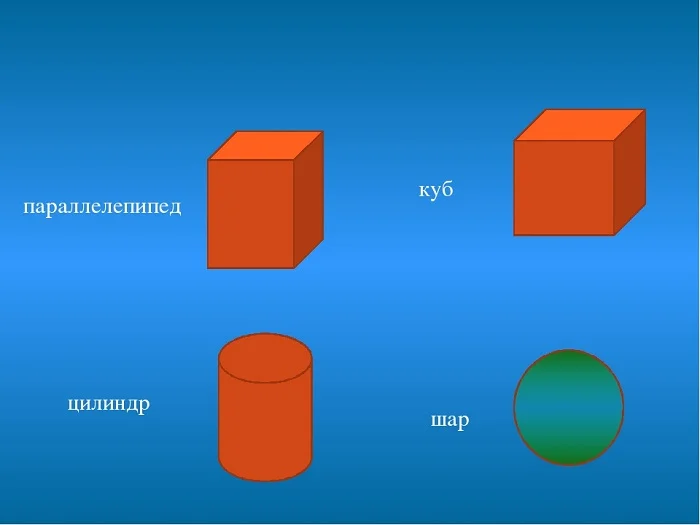(Источник)

Объем любого тела измеряется в кубических метрах (есть кратные и дольные единицы). Из математики известны формулы объемов:

V_пар = а ∙ в ∙ с (произведение длины, ширины и высоты),

V_к = а3 (а — ребро куба),

V_цил = π ∙ r2 ∙ h (r — радиус основания, h – высота цилиндра),

V_ш = 4/3 π ∙ R3 (R – радиус шара).

О вычислении объемов более сложной, но правильной, формы рассказывается в старших классах. А как определить объем, например, камня, форма которого может быть самой различной? Для измерения объемов таких тел используется специальный и очень простой прибор, который называется мензурка (или измерительный цилиндр). Это стеклянный сосуд с делениями. При помощи этого цилиндра легко найти объемы сыпучих тел и жидкостей. Для этого достаточно их засыпать вещество или налить в мензурку жидкость и, зная цену деления, определить объем.

(Источник)

На мензурке обычно ставится единица измерения в миллилитрах. Литр – это широко применяемая единица объема, равная одной тысячной кубического метра. 1 мл = 1 см3 = 10-6 м3.

Определить объем камня или любого другого тела неправильной формы с помощью мензурки можно при условии, что тело имеет размеры, позволяющие опустить его в мензурку.

(Источник)

Налить в мензурку воду и зафиксировать ее объем. Прикрепить тело неправильной формы к нити

Осторожно опустить полностью в воду. Уровень воды поднимется ровно на столько, чему равен объем тела

Пользуясь измерительным цилиндром, нельзя забывать, что это прибор, имеющий шкалу, а значит, результат получится с погрешностью.

ГЛАВА 3. Давление твердых тел, жидкостей и газов

§35. Давление. Единицы давления

Вопросы

1. Приведите примеры, показывающие, что действие силы зависит от площади опоры, на которую действует эта сила

Ответ:

2. Почему человек, идущий на лыжах, не проваливается в снег?

Ответ:

3. Почему острая кнопка легче входит в дерево, чем тупая?

Ответ:

4. На каком опыте можно показать, что действие силы зависит от площади опоры?

Ответ:

5. Какие вы знаете единицы давления?

Ответ:

Упражнение 14

1. Выразите в паскалях давление: 5 гПа; 0,02 Н/$cм^{2}$; 0,4 кПа; 10 Н/$cм^{2}$. Выразите в гектопаскалях и килопаскалях давление: 10 000 Па; 5800 Па.

Ответ:

2. Гусеничный трактор ДТ−75М массой 6610 кг имеет опорную площадь обеих гусениц 1,4 $м^{2}$. Определите давление этого трактора на почву. Во сколько раз оно больше давление, производимого мальчиком (см. пример в §35)?

Ответ:

3. Человек нажимает на лопату силой 600 Н. Какое давление оказывает лопата на почву, если ширина её лезвия 20 см, а толщина режущего края 0,5 мм? Зачем лопаты остро затачивают?

Ответ:

4. Мальчик массой 45 кг стоит на лыжах. Длина каждой лыжи 1,5 м, ширина 10 см. Какое давление оказывает мальчик на снег? Сравните его с давлением, которое производит мальчик, стоящий без лыж.

Ответ:

Задание

• В стеклянную ёмкость насыпьте песка. Наполните пластиковую бутылку с длинным горлышком водой, закройте крышкой и поставьте на песок. Затем переверните бутылку вверх дном и снова поставьте на песок. Объясните, почему во втором случае бутылка глубже вошла в песок.

Ответ:

Преимущества онлайн-пособия по Физике для 7 класса Перышкин, Вертикаль Базовый уровень Дрофа

Онлайн-гдз станут незаменимым помощником в изучении этого увлекательного предмета. Объемная и информационно насыщенная, она предоставит ребятам возможность более глубокого погружения в материал и углубленного понимания важнейших тем. На уроках ученики будут знакомиться с новым материалом и в дальнейшем глубже изучать следующие темы дома. Кинематика точки и твердого тела – одна из важнейших тем в физике. Ребята будут изучать различные аспекты движения объектов и его характеристики. Относительность движения также является неотъемлемой частью физики. Ученики смогут понять, как взаимосвязаны движущиеся объекты и как меняется их взаимное положение. Нужно знать каждому учащемуся:

1. Этот сборник был разработан известными и опытными методистами, которые обладают богатым опытом в области физики для старшей школы. Вся информация, представленная в онлайн-гдз, неоднократно проверена и прошла проверку на достоверность.
2. Неоспоримым преимуществом этого сборника является его соответствие требованиям Федерального государственного образовательного стандарта (ФГОС). Это гарантирует, что все представленные материалы не только полно исследованы, но и соответствуют актуальным нормам и стандартам образования.
3. Этот сборник, содержащий верные ответы и решения, может быть полезен не только учащимся, но и учителям в их профессиональной деятельности. Благодаря обширному спектру упражнений, представленных в данной тетради, вы сможете найти решения заданий любой степени сложности.

Таким образом, этот сборник может стать незаменимым помощником в освоении физики для всех старшеклассников и учителей в их учебном процессе.

Приборы для измерения сопротивления

Один из самых простых и распространенных приборов для измерения сопротивления – это мультиметр. Он удобен в использовании, так как позволяет измерить не только сопротивление, но и другие параметры, такие как напряжение и ток. Для измерения сопротивления мультиметр использует функцию «омметра».

Еще одним прибором, которым можно измерить сопротивление, является резисторметр. Он содержит известное сопротивление и позволяет определить неизвестное сопротивление, сравнивая их. Резисторметры часто используются в производстве для контроля качества электронных компонентов.

Кроме того, есть специальные приборы для измерения сопротивления в электронике. Например, омметры – приборы, которые позволяют измерить сопротивление небольших электрических цепей. Они удобны в использовании благодаря своей компактности и точности.

Итак, существует множество приборов для измерения сопротивления, как в домашних условиях, так и в научных и производственных целях. Каждый из них имеет свои преимущества и недостатки, но все они позволяют измерить сопротивление и получить точные результаты.

Достоинства онлайн-помощника по физике за 7 класс Перышкина

Усвоить сложную дисциплину поможет дополнительный материал. Он содержит развернутые правильные ответы на каждое задание изучаемых тем и поможет семикласснику качественно усвоить и закрепить пройденные разделы. При помощи сборника любой учащийся сможет:

• с большим интересом самостоятельно выполнять домашнее задание;
• намного лучше подготовиться к следующему уроку;
• повысить свою успеваемость.

Онлайн-формат дает возможность использовать материал с компьютера, ноутбука, планшета или телефона, а также сокращает время на поиске нужных ответов.

Учитель-предметник вполне может рассматривать данное пособие как некую методичку для составления своей программы, которая привлечет особое внимание и вовлечет в учебный процесс каждого ученика в классе

Числа «карлики» и числа «великаны»

Солнечная система.                                                        Лапка мухи под микроскопом. 

Чтобы достать до Альфа Центавры, звезды, ближайшей к Солнечной системе, надо со скоростью света (300 000 км/с) лететь четыре года. Расстояния до небесных тел огромны.

К звездам. (Источник)

Если определить расстояние от Земли до Солнца, то оно выразится числом 150 000 000 000 м. А бывают числа с еще большим количеством нулей. Масса Земли в килограммах выражается числом с 24 нулями. Такие числа называют «гигантами». Их записывать и использовать очень неудобно.

Существует способ краткой записи больших чисел в виде степени. Например, 1 000 000 = 106. 10 – основание, а 6 – показатель степени.

Используя этот способ, расстояние от нашей планеты до Солнца запишется так:

150 000 000 000 = 15 ∙ 1010 м – это промежуток называется астрономической единицей (1 а.е.) и служит единицей сравнения в Солнечной системе.

До Альфа-Центавры расстояние в 270 000 а.е., или 4 световых года. Световой год – это тоже астрономическая единица измерения расстояния. Астрономия – наука о космосе и космических телах. (1 св. год = 9,46 ∙ 1015 м = 68 000а.е.).

Фото двойной звезды Альфа созвездия Центавра. (Источник)

Большие числа записываются при помощи кратных приставок. Например, километр – это тысяча метров, килограмм – тысяча граммов. Приставка «кило» обозначает «тысяча». Есть и другие приставки, которые обозначают умножение величины на число, кратное десяти. Примеры и форма записи даны в таблице кратных приставок.

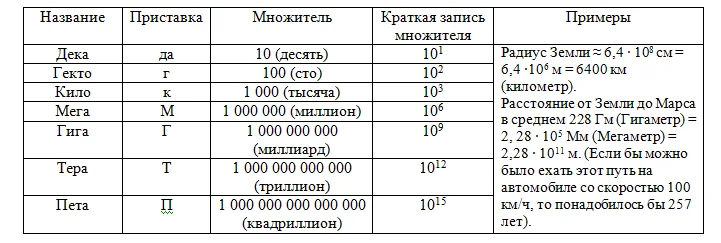
Используя эти приставки можно записывать очень большие числа.

1 а.е. = 150 000 000 000 м = 150 ∙ 109 м = 150Гм;

1 св. год = 9 460 000 000 000 м = 9,46 ∙ 1012 м = 9,46 Тм;

А теперь о числах – «карликах». Если сделать попытку измерить толщину одного листа книги, то сразу это не получится. Надо действовать по простому плану:

• отобрать в книге некоторое число страниц N (N = 100, например);
• измерить толщину L этих страниц (пусть L = 11 мм);
• найти толщину одной страницы d по формуле d = L/N.

Получится d = 0,11 мм = 0, 00011 м. Это число очень маленькое.

Такой способ измерения малых величин называется методом рядов. Он достаточно прост.

Размеры пшена.                                           Толщина проволоки. 

Но существуют и гораздо меньшие величины. Маленькие числа, так называемые «карлики», также записывают при помощи степеней или дольных приставок. (С приставками деци, санти, милли знакомятся еще в начальной школе).

Число меньше единицы, поэтому показатель степени – отрицательное число. Оно показывает количество цифр после запятой. Например, 0, 00011 м = 11 ∙ 10-5 м.

Число 0,00000625 можно записать по-разному, применяя степень:

625 ∙ 10-8, 62,5 ∙ 10-7, 6,25 ∙ 10-6 и т. д.

Очень маленькие числа по-другому можно записывать, используя таблицу дольных приставок.

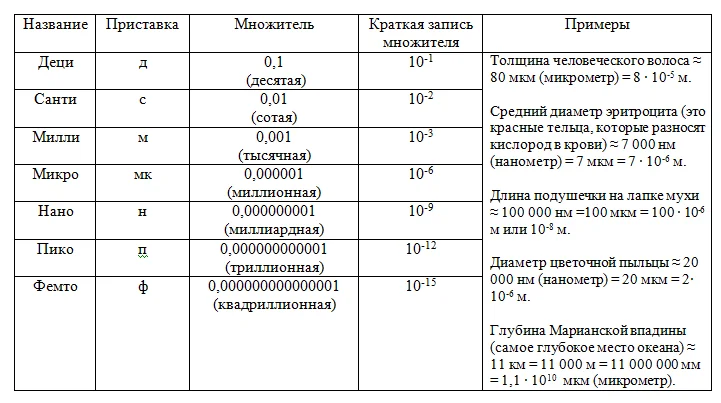
Например, при изготовлении сверхточных приборов (телескопов, микроскопов и др.), детали ошлифовываются до очень гладкой поверхности. Неровности должны быть меньше 2,5 ∙ 10-6 м или 2,5 мкм.

Большие и маленькие числа помогают человеку в различных отраслях деятельности: в науке, промышленности, медицине и т.д.

ГЛАВА 4. Работа и мощность. Энергия

§55. Механическая работа. Единицы работы

Вопросы

1. Какие два условия необходимы для совершения механической работы?

Ответ:

2. От каких двух величин зависит совершённая работа?

Ответ:

3. Что принимают за единицу работы?

Ответ:

4. Дайте определение единицы работы 1 Дж. Какие ещё единицы работы вы знаете?

Ответ:

Упражнение 30

1. В каких из нижеперечисленных случаев совершается механическая работа: мальчик влезает на дерево; девочка играет на пианино; вода давит на стенку сосуда; вода падает с плотины?

Ответ:

2. По гладкому горизонтальному льду катится стальной шарик. Допустим, что сопротивление движению шарика (трение о лёд, сопротивление воздуха) отсутствует. Совершается ли при этом работа?

Ответ:

3. При помощи подъёмного крана подняли груз массой 2500 кг на высоту 12 м. Какая работа при этом совершается?

Ответ:

4. Какая работа совершается при подъёме гидравлического молота массой 20 т на высоту 120 см?

Ответ:

Задание

1. Вычислите механическую работу, которую вы совершаете, равномерно поднимаясь с первого на второй этаж здания школы. Все необходимые данные получите сами, результат запишите в тетрадь.

Ответ:

2. Рассчитайте, какую механическую работу вы совершаете, равномерно проходя 1 км пути по горизонтальной дороге. Результаты запишите в тетрадь.Указание. Человек, равномерно идя по ровному горизонтальному пути, совершает примерно 0,05 той работы, которая требовалась бы для поднятия этого человека на высоту, равную длине пути.

Ответ:

Площадь и ее измерение

С измерением длин очень тесно связано измерение площадей. Из математики известны формулы площадей квадрата и прямоугольника. У квадрата все стороны равны, поэтому достаточно измерить одну сторону, а у прямоугольника противоположные стороны равны, поэтому надо знать длину и ширину. Площадь обозначается буквой S, и формулы для расчета площадей следующие:

S_кв = a2, S_пр = а ∙ в. Единицей измерения площади является квадратный метр (м2).

Для измерения малых площадей применяются см2 и мм2, а большие площади – в км2. В сельском хозяйстве для измерения земельных участков используют внесистемные единицы: гектар (га) – для больших, ар (а) или «сотка» — для небольших (приусадебных или дачных) участков земли. 1га = 10 000 м2, 1 а = 100 м2.

Очень часто на практике имеют дело с различными кругами. Это может быть цирковая арена, крышка стола, разрез ствола дерева. Формула нахождения площади круга: S = πR2. (π (пи) – это бесконечная дробь ≈ 3,14 подробно изучается в курсе алгебры).

Арена цирка.                                    Круглый стол.                            Спил дерева.  

А как определить площадь, ограниченную произвольной кривой линией? Такая площадь может быть у озера, полянки в лесу, листочка с дерева.

 

Существует правило нахождения площади тел произвольной формы:

• Разбить всю поверхность на равные квадраты с известной площадью.
• Подсчитать количество целых квадратов.
• Подсчитать число нецелых квадратов и поделить это число на два. (Это будет примерное количество целых квадратов).
• Сложить результаты пунктов 2 и 3.
• Умножить площадь одного квадрата на общее число целых квадратов.

Площадь больших территорий изображают в условном масштабе или фотографируют, применяют прием разбиения на квадраты и находят площадь фотографии. Используя масштаб вычисляют реальную площадь поверхности.

 

Довольно часто площадь приходится находить в географии. Каждое государство, область, город имеют свои площади. В строительстве – любое здание имеет площадь, которую необходимо знать строителям. В сельском хозяйстве ведется постоянный учет площадей для посевных культур.

ЛАБОРАТОРНЫЕ РАБОТЫ

№1 Определение цены деления измерительного прибора

Цель работы:Определить цену деления измерительного цилиндра (мензурки), научиться пользоваться им и определять с его помощью объём жидкости.Приборы и материалы:Измерительный цилиндр (мензурка), стакан с водой, небольшая колба и другие сосуды.Указания к работе:1. Рассмотрите измерительный цилиндр (рис

198), обратите внимание на его деления. Ответьте на следующие вопросы.1) Какой объём жидкости вмещает измерительный цилиндр, если жидкость налита:а) до верхнего штриха;б) до первого снизу штриха, обозначенного цифрой, отличной от нуля?2)Какой объём жидкости помещается:а) между 2−м и 3−м штрихами, обозначенными цифрами;б) между соседними (самыми близкими) штрихами мензурки?2

Как называется последняя вычисленная вами величина? Как определяют цену деления шкалы измерительного прибора?Запомните: прежде чем проводить измерения физической величины с помощью измерительного прибора, определите цену деления его шкалы.3. Рассмотрите рисунок 7 учебника и определите цену деления изображённой на нём мензурки.4. Налейте в измерительный цилиндр воды, определите и запишите, чему равен объём налитой воды.Примечание. Обратите внимание на правильное положение глаза при отсчёте объёма жидкости. Вода у стенок сосуда немного приподнимается, в средней же части сосуда поверхность жидкости почти плоская. Глаз следует направить на деление, совпадающее с плоской частью поверхности (рис. 198).5

Налейте полный стакан воды, потом осторожно перелейте воду в измерительный цилиндр. Определите и запишите с учётом погрешности, чему равен объём налитой воды

Вместимость стакана будет такой же.6. Таким же образом определите вместимость колбы, аптечных склянок и других сосудов, которые находятся на вашем столе.7. Результаты измерений запишите в таблицу 6.рис. 198.Таблица 6.

Ответ:

 Имея в распоряжении сосуд для измерения необходимо в первую очередь узнать шкалу его деления. Мы знаем, что для того чтобы найти деление без маркировки необходимо взять две известные метки с промаркированными делениями, найти их разницу и поделить пополам. На нашей шкале цилиндра возьмём, к примеру, числа 40 и 50.Получается, что цена каждого деления будет равна$\frac{50 — 40}{2} = \frac{10}{2}$ = 5 мл.В итоге мы нашли, что цена деления для цилиндра 5 мл. Можем начинать отвечать на вопросы лабораторной работы.1.

1, а) В случае уровня жидкости до верхнего штриха, в цилиндре налито 50 мл жидкости.1, б) В случае уровня жидкости до первого снизу штриха, обозначенного цифрой, отличной от нуля, в цилиндре налито 10 мл жидкости.2, а) В случае уровня жидкости между 2− м и 3−м штрихами, обозначенными цифрами, помещается 10 мл жидкости (например, возьмём штрихи 40 мл и 50 мл).2, б) В случае уровня жидкости между соседними (самыми близкими) штрихами мензурки (например, возьмём штрихи 50 и 55), помещается 5 мл жидкости.2. Вычисленная последняя нами величина называется ценой деления измерительного прибора, в данном случае цилиндра.3. На рисунке 7 изображен измерительный цилиндр.

Мы знаем, что для того чтобы найти деление без маркировки необходимо взять две известные метки с промаркированными делениями, найти их разницу и поделить пополам. На нашей шкале цилиндра возьмём, к примеру, числа 40 и 50.Получается, что цена каждого деления будет равна$\frac{50 — 40}{2} = \frac{10}{2}$ = 5 мл.В итоге мы нашли, что цена деления для цилиндра 5 мл.4. Объём налитой воды равен 35 мл или 35 $см^{3}$ .5. Из учебника мы знаем, что погрешность измерений прибора равна половине цены его деления шкалы. В нашем случае цена деления цилиндра − 5 мл, а значит погрешность измерения цилиндра равна $\frac{5}{2}$ мл = 2,5 мл.В итоге получится, что объём налитой в полный стакан воды будет равен 200 мл ($см^{3}$). при этом погрешность равна ±∆2,5 мл, то есть (200±∆2,5) мл ($см^{3}$)6.

Проводим измерения

Таблица 6.№           Название   Объём                  Вместимостьопыта    сосуда         жидкости $V_{ж}, см^{3}$    сосуда, $V_{с}, см^{3}$ |1             стакан           200                       200 2             колба             50                        50 3             пузырёк         30                        30 

Вывод. По результатам лабораторной работы научились на практике пользоваться измерительным прибором — цилиндр, нашли его цену деления и возможную погрешность при измерении объема жидкостей.

Приборы для измерения напряжения

Когда мы говорим о приборах для измерения напряжения, мы обычно имеем в виду вольтметры. Это устройства, которые позволяют измерить разность потенциалов между двумя точками в электрической цепи. Вольтметры бывают различных типов: аналоговые, цифровые, мультиметры.

Аналоговые вольтметры используют стрелку и шкалу для отображения измеряемого напряжения. Они достаточно просты в использовании и могут быть полезными для начинающих. Однако они не всегда точны и могут быть подвержены погрешностям.

Цифровые вольтметры, с другой стороны, показывают измерения в цифровой форме на своем экране. Они обычно более точные и надежные, а также обладают другими дополнительными функциями, такими как измерение сопротивления и тока. Эти приборы могут быть очень удобными для профессиональной работы или для точных измерений.

Мультиметры — это комплексные приборы, которые объединяют в себе функции вольтметра, амперметра и омметра. Это многофункциональные инструменты, которые позволяют измерять различные параметры электрической цепи. Они могут быть полезными для электротехников и людей, работающих с электроникой.

В итоге, при выборе прибора для измерения напряжения, важно учитывать его точность, надежность и дополнительные функции, которые могут быть полезными в вашей работе или учебе. Независимо от того, какой прибор вы выберете, помните, что правильное измерение напряжения является ключевым для эффективной работы с электрическими цепями и устройствами

Будьте осторожны и точны!