Вращательное движение тела
При изучении темы ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА вы научитесь решать простые задачи кинематики тела. В таких задачах вводятся векторные величины — угловая скорость
ПОСТАНОВКА ЗАДАЧИ. Твердое тело вращается вокруг неподвижной оси. Заданы некоторые кинематические характеристики движения тела и (или) кинематические характеристики движения точки этого тела. Найти остальные кинематические характеристики движения тела или точки.
Пусть тело вращается вокруг оси z. Кинематические характеристики движения тела:
- — угол поворота
- — угловая скорость
- — угловое ускорение
Кинематические характеристики точки на теле:
- — радиус траектории (расстояние до оси вращения) R:
- — скорость
- — ускорение
1. Записываем систему уравнений для всех величин, входящих в условие задачи. В зависимости от условия возможны три основных варианта решения. Гл.7.Вращательное движение тела
— Неизвестный закон вращения. Записываем систему двух уравнений для скорости
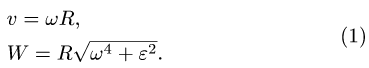
Для решения задачи необходимо, чтобы три из пяти величин
— Вращение с постоянной угловой скоростью. Интегрируя уравнение
Как правило, отсчет ведется от
— Вращение с постоянным угловым ускорением. Дважды интегрируя уравнение
получаем, при
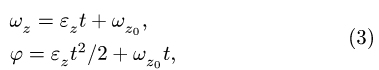
где
2. Решаем систему. Находим искомые величины.
Замечание. Ряд величин задан в тексте задач неявно. Например, угол поворота
Задача №5
Диск вращается вокруг неподвижной оси с постоянным угловым ускорением
1. В задаче задано постоянное угловое ускорение. Записываем систему уравнений для величин, входящих в условие задачи:
По условию задачи диск в начальный момент находился в покое, следовательно,
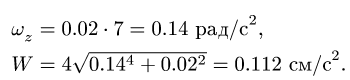
Ответ.
Передача вращения
Постановка Задачи. Механизм состоит из вращающихся на неподвижных осях блоков и поступательно движущихся элементов. Все элементы находятся во фрикционном, зубчатом или ременном зацеплениях. Задана какая-либо кинематическая характеристика одного из тел. Найти кинематические характеристики других тел.
1. Определяем кинематические характеристики тела, с заданным законом движения. Если это тело движется прямолинейно поступательно, то скорость и ускорение любой его точки имеет вид
где
где
2. Определяем угловую скорость тела, связанного нерастяжимой нитью (ремнем, тросом), фрикционно или зубчатым зацеплением с телом, угловая скорость которого известна:
где
в которое вместо радиусов
Если поступательное движение тела 1 передается вращательному движению тела 2 (или наоборот), то связь линейной и угловой скоростей имеет вид
где
3. Повторяя п.2 для всех пар кинематически связанных тел, составляем и решаем систему уравнений для неизвестных линейных и угловых скоростей.
4. Дифференцируя уравнения полученной системы, получаем аналогичную систему для угловых и линейных ускорений. Например, из уравнения (1) следует, что
Аналогично, из (2) следует связь линейного ускорения поступательно движущегося тела и углового ускорения связанного с ним вращающегося тела:
где
Задача №6
Механизм состоит из двух колес 1, 3 и блока 2, вращающихся на неподвижных осях. Ведущее колесо 1 механизма соединено ремнем с внутренним ободом блока 2. Внешний обод блока находится во фрикционном зацеплении с колесом 3 (рис. 84). Проскальзывание в точке зацепления отсутствует, ремень считать нерастяжимым.
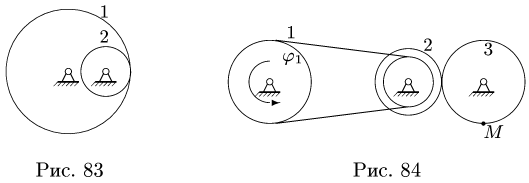
Задан закон движения ведущего колеса:
1. Находим угловую скорость ведущего колеса 1:
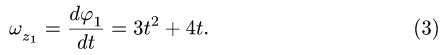
2. Определяем угловую скорость блока 2, связанного нерастяжимым ремнем с колесом 1:
где
3. Колеса 2 и 3 находятся во внешнем зацеплении и вращаются в разные стороны
Уравнения (3-5) образуют систему, решая которую, при t = 0.5 с, получаем
4. Дифференцируя уравнения системы (3-5), получаем аналогичную систему для угловых ускорений:
Решаем систему уравнений для ускорений (6) и получаем
Вычисляем ускорение точки М:
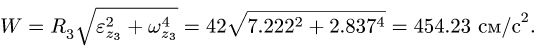
Ответ.
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Равновесие тяжелой рамы
- Расчет составной конструкции
- Момент силы относительно оси
- Равновесие вала
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Определение передаточных отношений различных передач
- Задачи на поступательное движение тела
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Где используются знания величин I для цилиндров?
Пожалуй, основной областью применения изложенной выше теории является автомобильная промышленность. В частности, коленчатый вал автомобиля снабжен тяжелым сплошным маховиком, имеющим цилиндрическую форму. Необходим маховик для того, чтобы обеспечить максимальную плавность вращения коленчатого вала, что отражается на плавности автомобильного хода. Маховик гасит любые большие угловые ускорения как во время разгона транспортного средства, так при его торможении.
Из формулы выше для момента инерции I1 понятно, что для увеличения этой величины выгоднее увеличить радиус, чем массу цилиндра (маховика). Так, удвоение массы приведет лишь к удвоению момента инерции. Однако если увеличить в два раза радиус, то I1 возрастет аж в 4 раза, что обеспечит более эффективное использование маховика.
Задача по физике — 1795
ГЛАВНАЯ » РЕШЕБНИК
2017-01-04 Даны два цилиндра одинаковых размеров и из одного и того же материала. Один цилиндр сплошной, другой сборный, состоящий из двух цилиндров, почти без зазора вложенных один в другой, причем трение между внешним и внутренним цилиндрами отсутствует (рис.). Какой из цилиндров будет быстрее скатываться без скольжения по одной и той же наклонной плоскости? Какое положение будет занимать при скатывании внутренний цилиндр, если он не совсем плотно входит во внешний?
Решение: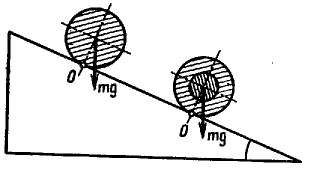
Качение без скольжения можно рассматривать как вращение вокруг мгновенной оси О (образующей цилиндра, касающейся в данный момент наклонной плоскости) и поступательное движение этой оси. Вращающим моментом при этом является момент силы тяжести $mg$ относительно оси О (рис.). Массы цилиндров, а значит, и их силы тяжести равны, поэтому и вращающие моменты для обоих цилиндров равны. Однако их моменты инерции различны.
Во втором (сборном) цилиндре играет роль момент инерции лишь наружного цилиндра, так как внутренний цилиндр, вследствие отсутствия сил трения, не вращается. Очевидно, что момент инерции первого (сплошного) цилиндра больше, чем момент инерции внешнего полого цилиндра во втором случае. При одном и том же вращающем моменте угловое ускорение обратно пропорционально моменту инерции цилиндра. Поэтому угловое ускорение сборного цилиндра больше, т. е. он скатывается быстрее.
Положение внутреннего цилиндра в зазоре можно определить из следующих соображений. Если бы внутренний цилиндр скользил без трения по наклонной плоскости, то его ускорение под действием силы тяжести было бы бблъшим, чем ускорение центра скатывающегося цилиндра. Это видно хотя бы из того, что потенциальная энергия, которой обладает цилиндр в ноле тяжести, при скольжении превращается только в, кинетическую энергию поступательного движения, а при скатывании — в энергию и поступательного и вращательного движений. Следовательно, скорость, а значит, и ускорение поступательного движения при скольжении должны быть больше, чем при скатывании, Так как в случае сборного цилиндра оба они — и внешний и внутренний — опускаются с одинаковым ускорением, то, значит, внешний цилиндр замедляет движение внутреннего. А для этого сила $F$, с которой внешний цилиндр давит на внутренний, должна иметь составляющую $F_{1}$, направленную вдоль наклонной плоскости кверху, т. е. сила $F$ должна быть отклонена несколько назад от направления перпендикуляра к наклонной плоскости (рис.). Так как трения нет, то сила $F$ должна быть нормальна к поверхности цилиндров, и, чтобы при этом она была отклонена назад, цилиндры должны касаться друг друга по образующей, лежащей, во всяком случае, впереди радиуса, проведенного к точке касания внешнего цилиндра с наклонной плоскостью.
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Осевые моменты инерции некоторых тел
Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
Материальная точка массы m
На расстоянии r от точки, неподвижная
Полый тонкостенный цилиндр или кольцо радиуса r и массы m
Сплошной цилиндр или диск радиуса r и массы m
Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1
Сплошной цилиндр длины l, радиуса r и массы m
Ось перпендикулярна к цилиндру и проходит через его центр масс
Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m
Ось перпендикулярна к цилиндру и проходит через его центр масс
Прямой тонкий стержень длины l и массы m
Ось перпендикулярна к стержню и проходит через его центр масс
Тонкостенная сфера радиуса r и массы m
Ось проходит через центр сферы
Шар радиуса r и массы m
Конус радиуса r и массы m
Равнобедренный треугольник с высотой h, основанием a и массой m
Ось перпендикулярна плоскости треугольника и проходит через вершину
Правильный треугольник со стороной a и массой m
Ось перпендикулярна плоскости треугольника и проходит через центр масс
Квадрат со стороной a и массой m
Ось перпендикулярна плоскости квадрата и проходит через центр масс
Тонкостенный цилиндр (кольцо, обруч)
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
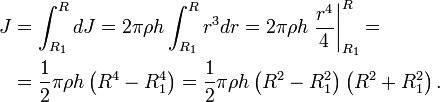
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
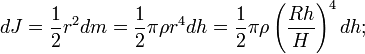
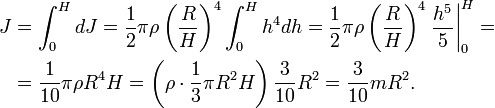
Сплошной однородный шар
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
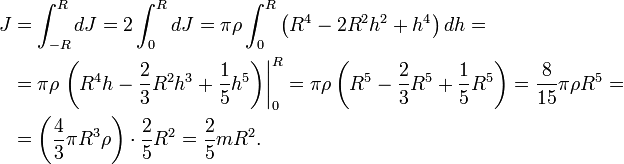
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
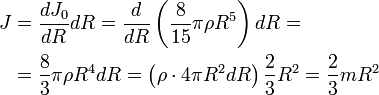
Тонкий стержень (ось проходит через центр)
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
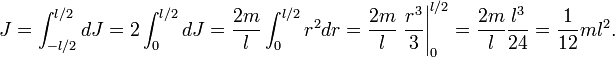
Тонкий стержень (ось проходит через конец)
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
Вычисляем момент инерции протяженного объекта
Момент инерции легко вычисляется для очень маленького (точечного) объекта, если все точки объекта расположены на одинаковом расстоянии от точки вращения. Например в предыдущем примере, если считать, что мячик для игры в гольф гораздо меньше длины нити, то все его точки находятся на одинаковом расстоянии от точки вращения, равном радиусу окружности вращения \( r \). В таком случае момент инерции имеет знакомый вид:
где \( r \) — это расстояние, на котором сосредоточена вся масса мячика \( m \).
Однако такая идеальная ситуация имеет место далеко не всегда. А чему равен момент инерции протяженного объекта, например стержня, вращающегося относительно одного из своих концов? Ведь его масса сосредоточена не в одной точке, а распределена по всей длине. Вообще говоря, для определения момента инерции протяженного объекта нужно просуммировать моменты инерции всех материальных точек объекта:
Например, момент инерции \( l \) системы из двух “точечных” мячиков для игры в гольф с одинаковой массой \( m \) на расстояниях \( r_1 \) и \( r_2 \) равен сумме их отдельных моментов инерции \( l_1=mr_1^2 \) и \( l_2=mr_2^2 \):
А как определить момент инерции диска, вращающегося относительно своего центра? Нужно мысленно разбить диск на множество материальных точек, вычислить момент инерции каждой такой точки и просуммировать полученные моменты инерции. Физики научились вычислять моменты инерции для многих объектов со стандартной формой. Некоторые из них приведены в табл. 11.1.
Попробуем вычислить моменты инерции нескольких предметов с простой геометрией.
Пример: замедление вращения компакт-диска
Компакт-диски могут вращаться с разными угловыми скоростями. Это необходимо для обеспечения одинаковой линейной скорости считывания информации на участках, находящихся на разных расстояниях от центра вращения. Пусть диск массой 30 г и диаметром 12 см сначала вращается со скоростью 700 оборотов в секунду, а спустя 50 минут — со скоростью 200 оборотов в секунду. Какой средний момент сил действует на компакт-диск при таком уменьшении скорости? Связь момента сил и углового ускорения имеет вид:
Момент инерции диска с радиусом \( r \), вращающегося относительно своего центра в плоскости диска, выражается формулой:
Подставляя значения, получим:
Теперь нужно определить угловое ускорение, которое определяется следующей формулой:
Изменение угловой скорости \( \Delta\omega \) произошло за промежуток времени:
В данном примере изменение угловой скорости:
где \( \omega_1 \) — конечная, а \( \omega_0 \) — начальная угловая скорость компакт-диска.
Чему они равны? Начальная скорость 700 оборотов в секунду означает, что диск за секунду 700 раз проходит \( 2\pi \) радиан:
Аналогично, конечная скорость 200 оборотов в секунду означает, что диск за секунду 200 раз проходит \( 2\pi \) радиан:
Подставляя значения в формулу углового ускорения, получим:
Подставляя значения момента инерции и углового ускорения в итоговую формулу момента силы, получим:
Итак, средний момент равен 10-4 Н·м, а чему будет равна сила для создания такого момента, если она приложена к краю диска? Ее величину легко вычислить по следующей формуле:
Оказывается, для такого замедления компакт-диска нужно приложить не такую уж и большую силу.
Еще один пример: поднимаем груз
Вращательное движение порой внешне выглядит не так очевидно, как вращение ком- пакт-диска. Например подъем груза с помощью блока также является примером вращательного движения. Хотя канат и груз движутся поступательно, но сам блок вращается (рис. 11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.
В данном примере нужно вычислить сумму всех моментов сил \( \mathbf{\sum\! M} \), которые действуют на веревку:
В данном примере на веревку действует два момента сил: один \( M_1 \) со стороны груза весом \( mg \), а другой \( M_2 \) — со стороны горизонтальной силы \( F \):
Отсюда получаем формулу для углового ускорения:
Эти моменты \( M_1 \) и \( M_2 \) имеют одинаковое плечо, равное радиусу блока \( r \), поэтому:
Поскольку блок имеет форму диска, то из табл. 11.1 находим его момент инерции:
Подставляя выражения для \( l \), \( M_1 \) и \( M_2 \) в формулу для углового ускорения, получим:
Подставляя значения, получим:
Момент инерции шара, теория и примеры
Это скалярная (в общем случае тензорная) величина. Для непрерывного однородного тела, вращающегося около оси, момент инерции определяют как:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.
Момент инерции однородного шара
Однородный по объем шар можно представить как систему сферических слоев (или тонких дисков), обладающих массами ().
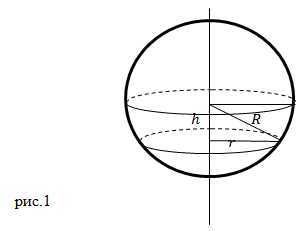
По условию шар является однородным, плотность его можно представить как:
где – объем всего шара; m – масса всего шара.
В качестве элементарной массы выберем сферический слой радиуса r (указанный на рис.1). Его массу можно представить как:
При этом объем рассматриваемого сферического слоя равен:
Момент инерции тонкого диска (толщина диска ) равен:
Выделенный нами диск находится на расстоянии h от центра шара. Радиус рассматриваемого нами диска связан с расстоянием h выражением:
Тогда формулу (4) преобразуем к виду:
Просуммируем моменты инерции всех дисков:
Получили, что момент инерции однородного шара, относительно его диаметра равен:
Момент инерции полого шара (сферы)
Момент инерции сферы удобно находить, используя полярный момент инерции. Это момент инерции тела относительно некоторой точки, назовем ее O. Он равен произведению всех масс точек тела на квадраты расстояний от них до точки О. Если через полюс О провести прямоугольные оси, то полярный момент () равен:
Полярный момент инерции равен половине суммы моментов инерции тела относительно трех прямоугольных осей, которые проходят через полюс:
В центре тяжести тела полярный момент инерции имеет минимальной значение.
Рассмотрим сферу радиуса R. Для нее удобно сначала найти полярный момент инерции относительно ее центра ():
Согласно формуле (10) и зная, что для сферы , имеем:
Получаем, что момент инерции сферы (полого шара) равен:
Цель работы – измерить моменты инерции различных тел. Проверить теорему Штейнера.
Общие сведения
Момент
инерции тела является мерой инертности тела при вращательном движении,
подобно тому, как масса тела является мерой инертности тела при поступательном
движении. Момент инерции тела зависит от размеров и формы тел и от
распределения массы тела относительно оси вращения. Для вычисления момента
инерции твердого тела относительно некоторой оси ОО разобьем мысленно тело на
большое число весьма малых элементов — материальных точек (рис.1). Тогда момент
инерции такой отдельной элементарной массы
где —
расстояние от элемента объема до оси вращения, r — плотность вещества.
Момент инерции всего тела
,
Таким
образом, момент инерции различных тел можно найти с помощью интегрирования.
Рассмотрим результаты расчета для
некоторых частных случаев.
1. Момент
инерции материальной точки массой m ,
находящейся на расстоянии R от оси вращения
(1)
2. Момент
инерции однородного диска относительно оси, перпендикулярной к плоскости диска
и проходящей через его центр. Радиус диска R, его масса m.
(2)
.Эта же формула справедлива для момента инерции
сплошного цилиндра относительно оси совпадающей с осью цилиндра..
3. Момент
инерции полого цилиндра с внутренним радиусом R1
и внешним радиусом R2 относительно
оси , совпадающей с осью цилиндра.
(3)
4. Момент инерции шара радиуса R относительно оси
проходящей через его центр.
(4)
5. Момент
инерции тонкого стержня относительно оси перпендикулярной к стержню и
проходящей через его середину. Длина стержня l,
(5)
Эти формулы
для моментов инерции относительно оси симметрии.
Момент инерции
относительно произвольной оси можно найти с помощью теоремы Штейнера:
Момент
инерции относительно произвольной оси О1О1 равен сумме
момента инерции I, относительно оси OO, параллельной данной и
проходящей через центр инерции тела и произведения массы тела на квадрат
расстояния d между осями.
Получим с помощью
этой теоремы формулу момента инерции стержня относительно оси перпендикулярной
к стержню и проходящей через его конец.
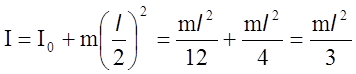(6)
В общем
случае расчет момента инерции представляет собой достаточно сложную задачу, и
часто он определяется экспериментально с помощью основного уравнения динамики
вращательного движения, методом крутильных колебаний и др.
В данной работе для экспериментального измерения
моментов инерции различных тел используется метод крутильных колебаний.
Исследуемые
тела насаживаются на ось спиральной пружины. Если зкрутить пружину на угол j, то в результате деформации пружины
возникнет упругая сила. Она создает крутящий момент (момент силы) М
M=Dj (7)
Здесь D – модуль кручения пружины.
Этот крутящий
момент стремится вернуть пружину в исходное (равновесное) состояние. В
результате возникают крутильные колебания.
Из теории
крутильных колебаний следует формула для периода колебаний
(8)
где J — момент инерции.
Отсюда
(9)
Таким образом,
измеряя период крутильных колебаний и зная модуль кручения D
пружины, можно вычислить момент инерции тела, насаженного на ось пружины.
Порядок
выполнения работы.
Для определения
модуля кручения D пружины возьмите стержень с грузами и насадите
его на ось пружины. Грузы сдвиньте к центру.
Поверните
стержень на 90о (p/2
радиан). Прикрепите к стержню (у края грузов) динамометр и измерьте силу F. Необходимую для удержания стержня в этом положении
(динамометр держите перпендикулярно стержню).
Вычислите
момент силы М
М=Fl
Здесь l – плечо силы, то есть расстояние от оси вращения до
места приложения силы (до места прикрепления динамометра).
Геометрические характеристики плоских сечений
При некоторых видах деформаций прочность и жесткость (способность противостоять деформации) элементов конструкций зависит не только от величины поперечного сечения, но и от формы этого сечения. 
Самый простой пример — обыкновенную школьную линейку можно легко изогнуть относительно широкой стороны поперечного сечения и совершенно невозможно изогнуть относительно его короткой стороны. При этом общая площадь сечения в обоих случаях одинакова. На основании этого примера становится очевидным, что на сопротивление некоторым видам деформации оказывает влияние (иногда — решающее) не только величина площади сечения бруса, но и его геометрическая форма.
При изучении деформаций изгиба и кручения нам потребуется знание некоторых геометрических характеристик плоских сечений, которые оказывают влияние на способность конструкций сопротивляться деформациям относительно той или иной оси либо полюса (точки).
Чтобы понять суть явления и влияния этих геометрических характеристик на сопротивление бруса, например, изгибу, следует обратиться к основополагающим постулатам сопромата. Как известно из установленного в 1660 году английским физиком Робертом Гуком закона, напряжение в сечениях бруса прямо пропорционально его относительному удлинению. Очевидно, что волокна, расположенные дальше от оси изгиба, растягиваются (или сжимаются) сильнее, чем расположенные вблизи оси. Следовательно, и напряжения возникающие в них будут бόльшими.
Можно привести условную сравнительную аналогию между напряжением в разных точках сечения бруса с моментом силы — чем больше плечо силы — тем больше ее момент (относительно оси или точки). Аналогично — чем дальше от какого-либо полюса (оси) отстоит точка в сечении, тем большее напряжение в ней возникает при попытке изогнуть или скрутить брус относительно этого полюса (оси).
***
Статический момент площади
Статическим моментом площади плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений элементарных площадок (Si) на расстояния (ri)от них до этой оси.
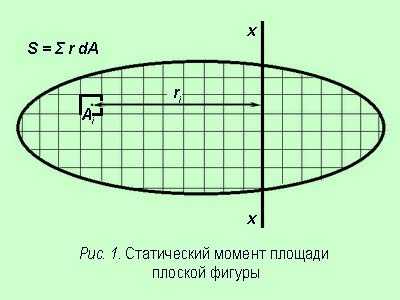
Если упростить это определение, то статический момент инерции плоской фигуры относительно какой-либо оси (лежащей в той же плоскости, что и фигура) можно получить следующим образом:
- разбить фигуру на крохотные (элементарные) площадки (рис. 1);
- умножить площадь каждой площадки на расстояние ri от ее центра до рассматриваемой оси;
- сложить полученные результаты.
Статический момент площади плоской фигуры обозначают S с индексом оси, относительно которой он рассматривается: Sx, Sy, Sz.
Sx = Σ y dA; Sy = Σ x dA.
Анализ этих формул позволяет сделать вывод, что статический момент площади фигуры относительно оси, лежащей в этой же плоскости, равен произведению площади фигуры на расстояние от ее центра тяжести до этой оси.
Из этого вывода следует еще один вывод — если рассматриваемая ось проходит через центр тяжести плоской фигуры, то статический момент этой фигуры относительно данной оси равен нулю.
Единица измерения статического момента площади — метр кубический (м3).
При определении статического момента площади сложной фигуры можно применять метод разбиения, т. е. определять статический момент всей фигуры, как алгебраическую сумму статических моментов отдельных ее частей. При этом сложная геометрическая фигура разбивается на простые по форме составные части — прямоугольники, треугольники, окружности, дуги и т. п., затем для каждой из этих простых фигур подсчитывается статический момент площади, и определяется алгебраическая сумма этих моментов.
***
Полярный момент инерции
Полярным моментом инерции плоской фигуры относительно полюса (точки), лежащего в той же плоскости, называется сумма произведений элементарных площадок (Si) этой фигуры на квадрат их расстояний (r2i) до полюса.
Полярный момент инерции обозначают Iρ (иногда его обозначают Jρ), а формула для его определения записывается так:
Iρ = Σ ρ2 dA.
Единица измерений полярного момента инерции — м4, из чего следует, что он не может быть отрицательным.
Понятие полярного момента инерции понадобится при изучении деформаций кручения круглых валов, поэтому приведем формулы для определения полярного момента квадратного, круглого и кольцевого сечения.