Что такое катушка индуктивности
Данный элемент ещё называют дросселем. Это свёрнутый в спираль изолированный провод. Для такой спирали характерны большие индуктивные и маленькие ёмкостные параметры.
Важно! Дроссель препятствует протеканию переменного тока, потому что обладает существенной инерционностью. Она препятствует любому изменению проходящего через витки тока. При этом нет разницы, увеличивается он или уменьшается
При этом нет разницы, увеличивается он или уменьшается.
В связи с этим данные элементы применяют в электротехнике для осуществления:
- токоограничения;
- ослабления биений;
- помехоподавления;
- формирования магнитного поля;
- изготовления датчиков движения.
Дроссель входит в систему колебательного контура в цепях резонанса и применяется в линиях задержки.
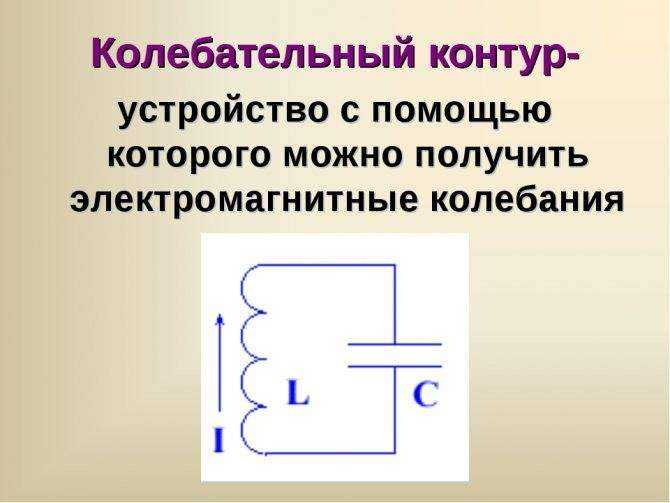
Провод намотки катушки
Для навивки спиралей катушек со скользящими контактами, работающих в каскадах мощностью более 2кВт, используются трубки квадратного и прямоугольного сечения. Конструкция контактной системы при этом более простая, а сама катушка получается более устойчивой и жесткой. Широкие медные ленты (шины) прямоугольного сечения применяются главным образом для навивки спиралей плоских катушек индуктивности каскадов мощностью до 5кВт. Цилиндрические катушки индуктивности, спирали которых навиты такой лентой, используются в каскадах мощностью не более 1 кВт. Из трубки круглого сечения навивают в основном катушки постоянной индуктивности, вариометры, а также катушки переменной индуктивности с короткозамкнутым витком.
Большое значение имеет чистота поверхности спирали, которая должна быть возможно более высокого класса. Плохая чистота поверхности приводит к ускоренному истиранию контактов токосъема и, как следствие, к возрастанию переходного сопротивления, уменьшению добротности контура и снижению надежности в эксплуатации (у передатчиков средней мощности переходное сопротивление составляет от 0,01 до 0,05 Ом). Кроме того, повышение чистоты поверхности уменьшает поверхностное сопротивление спирали, так как путь тока в проводнике с идеально ровной поверхностью короче, чем в проводнике с шероховатой поверхностью. Увеличение сопротивления становится заметным, когда высота микронеровностей соизмерима с глубиной проникновения тока в провод (у медного провода в диапазоне частот 1,5-30МГц глубина проникновения тока составляет 0,05- 0,01 мм).
При расчете катушек индуктивности исходными данными являются максимальная величина индуктивности , амплитуда переменного напряжения на катушке и эффективное значение тока через катушку. Как известно из теории поверхностного эффекта (скин–эффекта), сопротивление провода на высоких частотах следует рассчитывать не по его сечению, а по периметру. При этом необходимо учитывать реальные условия нагрева и теплоотдачи провода. Для расчета катушки вводят понятие перегрева провода , где — температура поверхности провода, a — температура окружающей среды. Обычно принимают 30-40,°С. Требуемый диаметр медного провода определяется по полуэмпирической формуле:
d= 0,18, (9.1)
где – эффективное значение высокочастотного тока через катушку, А; f – рабочая частота, Гц; τ – перегрев провода,°C; d — диаметр провода, мм. При использовании провода намотки другого профиля периметр провода определяется формулой:
р=0,18π ( 9. 1’)
Если периметр р < 10мм, то применяют провод сплошного сечения, при периметре р> 10 мм – провод трубчатый. В том случае, когда спираль охлаждается водой, требуемая величина периметра, рассчитанная по формуле ( 9. 1’), может быть уменьшена в два – три раза, поскольку водой отводится около 95% тепла. Однако водяное охлаждение катушек индуктивности возможно только в каскадах, где используются радиолампы с водяным охлаждением. При курсовом и дипломном проектировании можно руководствоваться сортаментами квадратных и прямоугольных труб из меди марок Ml и М2, приведенными в табл. 9.1 и 9.2, где а, b и s – размеры, показанные на риc.9.2. Стандартными значениями диаметра d проводов круглого сечения (рис.9.2) являются: 1; 1,12; 1,25, 1,4; 1,5; 1,68; 1,74; 1,81; 1,88; 1,95; 2,01; 2,26; 2,44; 2,63; 2,83; 3,05; 3,28; 3,53; 3,8; 4,1; 4,5; 4,8; 5,2 мм, и др.
Рис.2. Квадратное, прямоугольное и круглое сечения медной трубы
Таблица 9.1
|
А, мм |
10; 12 |
14; 16 |
18; 20 |
22; 25 |
28; 32; 36; 40 |
42; 45; 50 |
|
S, мм |
1; 1,5 |
1; 1,5; 2; 2,5 |
1; 1,5; 2; 2,5 |
1,5; 2; 2,5; 3 |
1,5; 2; 2,5; 3; 4; 5 |
1,5; 2; 2,5; 3; 4; 5 |
Таблица 9.2
|
а, мм |
b, мм |
s, мм |
|
130 |
65 |
2,5 |
|
160 |
80 |
2,5 |
|
180 |
85 |
3,0 |
Как рассчитать нагрев нихрома?
Электрическое сопротивление — это одна из самых важных характеристик нихрома.
Оно определяется многими факторами, в частности электрическое сопротивление нихрома зависит от размеров проволоки или ленты, марки сплава.
Общая формула для активного сопротивления имеет вид:
R = ρ · l / S
R — активное электрическое сопротивление (Ом), ρ- удельное электрическое сопротивление (Ом·мм), l- длина проводника (м), S — площадь сечения (мм2)
Значения электрического сопротивления для 1 м нихромовой проволоки Х20Н80
| 1 | Ø 0,1 | 137,00 |
| 2 | Ø 0,2 | 34,60 |
| 3 | Ø 0,3 | 15,71 |
| 4 | Ø 0,4 | 8,75 |
| 5 | Ø 0,5 | 5,60 |
| 6 | Ø 0,6 | 3,93 |
| 7 | Ø 0,7 | 2,89 |
| 8 | Ø 0,8 | 2,2 |
| 9 | Ø 0,9 | 1,70 |
| 10 | Ø 1,0 | 1,40 |
| 11 | Ø 1,2 | 0,97 |
| 12 | Ø 1,5 | 0,62 |
| 13 | Ø 2,0 | 0,35 |
| 14 | Ø 2,2 | 0,31 |
| 15 | Ø 2,5 | 0,22 |
| 16 | Ø 3,0 | 0,16 |
| 17 | Ø 3,5 | 0,11 |
| 18 | Ø 4,0 | 0,087 |
| 19 | Ø 4,5 | 0,069 |
| 20 | Ø 5,0 | 0,056 |
| 21 | Ø 5,5 | 0,046 |
| 22 | Ø 6,0 | 0,039 |
| 23 | Ø 6,5 | 0,0333 |
| 24 | Ø 7,0 | 0,029 |
| 25 | Ø 7,5 | 0,025 |
| 26 | Ø 8,0 | 0,022 |
| 27 | Ø 8,5 | 0,019 |
| 28 | Ø 9,0 | 0,017 |
| 29 | Ø 10,0 | 0,014 |
Значения электрического сопротивления для 1 м нихромовой ленты Х20Н80
| 1 | 0,1×20 | 2 | 0,55 |
| 2 | 0,2×60 | 12 | 0,092 |
| 3 | 0,3×2 | 0,6 | 1,833 |
| 4 | 0,3×250 | 75 | 0,015 |
| 5 | 0,3×400 | 120 | 0,009 |
| 6 | 0,5×6 | 3 | 0,367 |
| 7 | 0,5×8 | 4 | 0,275 |
| 8 | 1,0×6 | 6 | 0,183 |
| 9 | 1,0×10 | 10 | 0,11 |
| 10 | 1,5×10 | 15 | 0,073 |
| 11 | 1,0×15 | 15 | 0,073 |
| 12 | 1,5×15 | 22,5 | 0,049 |
| 13 | 1,0×20 | 20 | 0,055 |
| 14 | 1,2×20 | 24 | 0,046 |
| 15 | 2,0×20 | 40 | 0,028 |
| 16 | 2,0×25 | 50 | 0,022 |
| 17 | 2,0×40 | 80 | 0,014 |
| 18 | 2,5×20 | 50 | 0,022 |
| 19 | 3,0×20 | 60 | 0,018 |
| 20 | 3,0×30 | 90 | 0,012 |
| 21 | 3,0×40 | 120 | 0,009 |
| 22 | 3,2×40 | 128 | 0,009 |
Расчет нихромовой спирали
При намотке спирали из нихрома для нагревательных приборов эту операцию зачастую выполняют «на глазок», а затем, включая спираль в сеть, по нагреву нихромового провода подбирают требующееся количество витков. Обычно такая процедура занимает много времени, да и нихром расходуется попусту.
Чтобы рационализировать эту работу при использовании нихромовой спирали на напряжение 220 В, предлагаю воспользоваться данными приведенными в таблице, из расчета, что удельное сопротивление нихрома = (Ом · мм2 / м) C.
С ее помощью можно быстро определить длину намотки виток к витку в зависимости от толщины нихромового провода и диаметра стержня, на который наматывается нихромовая спираль.
Пересчитать длину спирали из нихрома на другое напряжение нетрудно, использовав простую математическую пропорцию.
Длина нихромовой спирали в зависимости от диаметра нихрома и диаметра стержня
| 1,5 | 49 | 1,5 | 59 | 1,5 | 77 | 2 | 64 | 2 | 76 | 2 | 84 | 3 | 68 | 3 | 78 |
| 2 | 30 | 2 | 43 | 2 | 68 | 3 | 46 | 3 | 53 | 3 | 64 | 4 | 54 | 4 | 72 |
| 3 | 21 | 3 | 30 | 3 | 40 | 4 | 36 | 4 | 40 | 4 | 49 | 5 | 46 | 6 | 68 |
| 4 | 16 | 4 | 22 | 4 | 28 | 5 | 30 | 5 | 33 | 5 | 40 | 6 | 40 | 8 | 52 |
| 5 | 13 | 5 | 18 | 5 | 24 | 6 | 26 | 6 | 30 | 6 | 34 | 8 | 31 | ||
| 6 | 20 | 8 | 22 | 8 | 26 | 10 | 24 |
Например, требуется определить длину нихромовой спирали на напряжение 380 В из провода толщиной 0,3 мм, стержень для намотки Ø 4 мм. Из таблицы видно, что длина такой спирали на напряжение 220 В будет равна 22 см. Составим простое соотношение:
220 В — 22 см
380 В — Х см
тогда:
X = 380 · 22 / 220 = 38 см
Намотав нихромовую спираль, подключите ее, не обрезая, к источнику напряжения и убедитесь в правильности намотки. У закрытых спиралей длину намотки увеличивают на 1/3 значения, приведенного в таблице.
Расчет массы нихрома Х20Н80 (проволока и лента)
В данной таблице приведена теоретическая масса 1 метра нихромовой проволоки и ленты. Она изменяется в зависимости от размеров продукции.
| Ø 0,4 | 8,4 | 0,126 | 0,001 |
| Ø 0,5 | 8,4 | 0,196 | 0,002 |
| Ø 0,6 | 8,4 | 0,283 | 0,002 |
| Ø 0,7 | 8,4 | 0,385 | 0,003 |
| Ø 0,8 | 8,4 | 0,503 | 0,004 |
| Ø 0,9 | 8,4 | 0,636 | 0,005 |
| Ø 1,0 | 8,4 | 0,785 | 0,007 |
| Ø 1,2 | 8,4 | 1,13 | 0,009 |
| Ø 1,4 | 8,4 | 1,54 | 0,013 |
| Ø 1,5 | 8,4 | 1,77 | 0,015 |
| Ø 1,6 | 8,4 | 2,01 | 0,017 |
| Ø 1,8 | 8,4 | 2,54 | 0,021 |
| Ø 2,0 | 8,4 | 3,14 | 0,026 |
| Ø 2,2 | 8,4 | 3,8 | 0,032 |
| Ø 2,5 | 8,4 | 4,91 | 0,041 |
| Ø 2,6 | 8,4 | 5,31 | 0,045 |
| Ø 3,0 | 8,4 | 7,07 | 0,059 |
| Ø 3,2 | 8,4 | 8,04 | 0,068 |
| Ø 3,5 | 8,4 | 9,62 | 0,081 |
| Ø 3,6 | 8,4 | 10,2 | 0,086 |
| Ø 4,0 | 8,4 | 12,6 | 0,106 |
| Ø 4,5 | 8,4 | 15,9 | 0,134 |
| Ø 5,0 | 8,4 | 19,6 | 0,165 |
| Ø 5,5 | 8,4 | 23,74 | 0,199 |
| Ø 5,6 | 8,4 | 24,6 | 0,207 |
| Ø 6,0 | 8,4 | 28,26 | 0,237 |
| Ø 6,3 | 8,4 | 31,2 | 0,262 |
| Ø 7,0 | 8,4 | 38,5 | 0,323 |
| Ø 8,0 | 8,4 | 50,24 | 0,422 |
| Ø 9,0 | 8,4 | 63,59 | 0,534 |
| Ø 10,0 | 8,4 | 78,5 | 0,659 |
| 1 x 6 | 8,4 | 6 | 0,050 |
| 1 x 10 | 8,4 | 10 | 0,084 |
| 0,5 x 10 | 8,4 | 5 | 0,042 |
| 1 x 15 | 8,4 | 15 | 0,126 |
| 1,2 x 20 | 8,4 | 24 | 0,202 |
| 1,5 x 15 | 8,4 | 22,5 | 0,189 |
| 1,5 x 25 | 8,4 | 37,5 | 0,315 |
| 2 x 15 | 8,4 | 30 | 0,252 |
| 2 x 20 | 8,4 | 40 | 0,336 |
| 2 x 25 | 8,4 | 50 | 0,420 |
| 2 x 32 | 8,4 | 64 | 0,538 |
| 2 x 35 | 8,4 | 70 | 0,588 |
| 2 x 40 | 8,4 | 80 | 0,672 |
| 2,1 x 36 | 8,4 | 75,6 | 0,635 |
| 2,2 x 25 | 8,4 | 55 | 0,462 |
| 2,2 x 30 | 8,4 | 66 | 0,554 |
| 2,5 x 40 | 8,4 | 100 | 0,840 |
| 3 x 25 | 8,4 | 75 | 0,630 |
| 3 x 30 | 8,4 | 90 | 0,756 |
| 1,8 x 25 | 8,4 | 45 | 0,376 |
| 3,2 x 32 | 8,4 | 102,4 | 0,860 |
Расчет массы вольфрамовой проволоки
| 8 | 0,008 | 0,19 | 0,0010 | 0,97 | 1031,32 |
| 9 | 0,009 | 0,25 | 0,0012 | 1,23 | 814,87 |
| 10 | 0,01 | 0,30 | 0,0015 | 1,52 | 660,04 |
| 11 | 0,011 | 0,37 | 0,0018 | 1,83 | 545,49 |
| 12 | 0,012 | 0,44 | 0,0022 | 2,18 | 458,36 |
| 13 | 0,013 | 0,51 | 0,0026 | 2,56 | 390,56 |
| 14 | 0,014 | 0,59 | 0,0030 | 2,97 | 336,76 |
| 15 | 0,015 | 0,68 | 0,0034 | 3,41 | 293,35 |
| 16 | 0,016 | 0,78 | 0,0039 | 3,88 | 257,83 |
| 17 | 0,017 | 0,88 | 0,0044 | 4,38 | 228,39 |
| 18 | 0,018 | 0,98 | 0,0049 | 4,91 | 203,72 |
| 19 | 0,019 | 1,09 | 0,0055 | 5,47 | 182,84 |
| 20 | 0,02 | 1,21 | 0,0061 | 6,06 | 165,01 |
| 30 | 0,03 | 2,73 | 0,0136 | 13,64 | 73,34 |
| 40 | 0,04 | 4,85 | 0,0242 | 24,24 | 41,25 |
| 50 | 0,05 | 7,58 | 0,0379 | 37,88 | 26,40 |
| 60 | 0,06 | 10,91 | 0,0545 | 54,54 | 18,33 |
Винтовая линия
Винтовая линия относится к пространственным кривым. Различают цилиндрические, конические, сферические и другие винтовые линии.
Цилиндрическая винтовая линия описывается точкой, которая совершает равномерное движение вдоль образующей кругового цилиндра, а образующая вращается с постоянной угловой скоростью вокруг оси цилиндра.
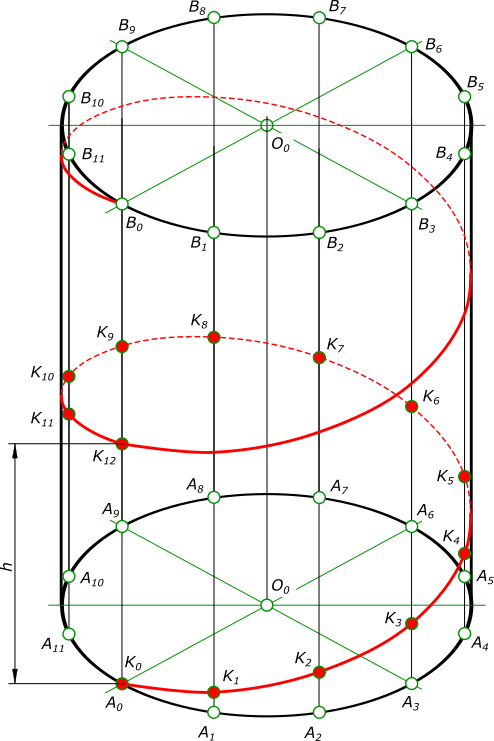
Образующая занимает 12 последовательных положений: A 0 B 0 . Дуги A 0 A 1 , A 1 A 2 A 2 A 3 и т. д. равны между собой и каждая равна pd/n, где d — диаметр цилиндра, p = 3,14 и n — число положений образующей цилиндра, принятое для построения. Пусть образующая занимает 12 последовательных положений: A 0 B 0 , A 1 B 1 , A 2 B 2 и т. д. Начальному положению образующей AB соответствует A 0 B 0 , а точки K — K 0 . При перемещении образующей AB в положение A 1 B 1 точка K займет положение K 1 , и поднимется по образующей на величину отрезка A 1 K 1 = h/12. При последующем перемещении образующая займет положение A 2 B 2 , а точка K положение K 2 и поднимется на высоту равную A 2 B 2 = 2A 1 B 1 = 2(h/12), и т. д. Когда образующая совершит полный оборот и снова займет начальное положение, точка K будет находится на ней на высоте A 12 B 12 = 12(h/12) = h, величине шага винтовой линии. При этом точка описывает кривую K 0 K 6 K 12 , длина которой равна длине одного витка. На практике эти движения достигаются на токарном станке, где острие резца соответствует данной точке.
Резец оставит на цилиндрической поверхности след — винтовую линию. Винтовая линия может быть правой или левой. Правой винтовой линией называют линию, совершающую подъем вокруг своей оси против часовой стрелки, а левой — винтовую линию, совершающую подъем по часовой стрелке. Правая цилиндрическая винтовая линия
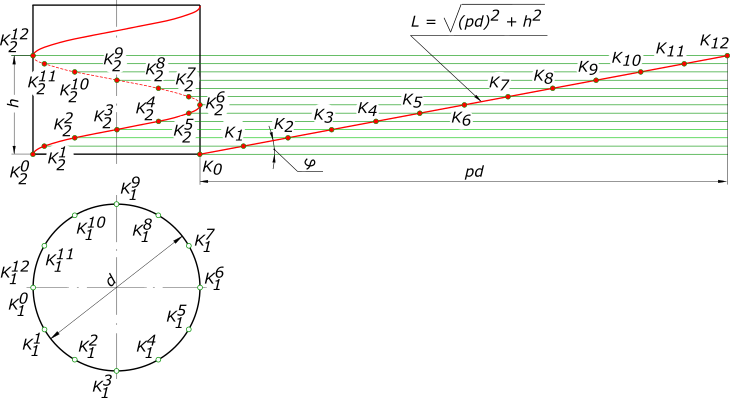
может быть построена, когда заданы ее элементы. Винтовая линия характеризуется следующими элементами: шаг, виток и угол подъема. Шагом винтовой линии называется расстояние между смежными витками, измеренное вдоль образующей кругового цилиндра. Витком называют винтовую линию, описанную точкой за один оборот образующей вокруг оси кругового цилиндра. Длина витка равна L. Углом подъема винтовой линии называют отношение tg(φ)= h/(pd), тогда φ = arctg(φ), где d — диаметр цилиндра, p=3,14.
Винтовая линия может быть получена на конической поверхности
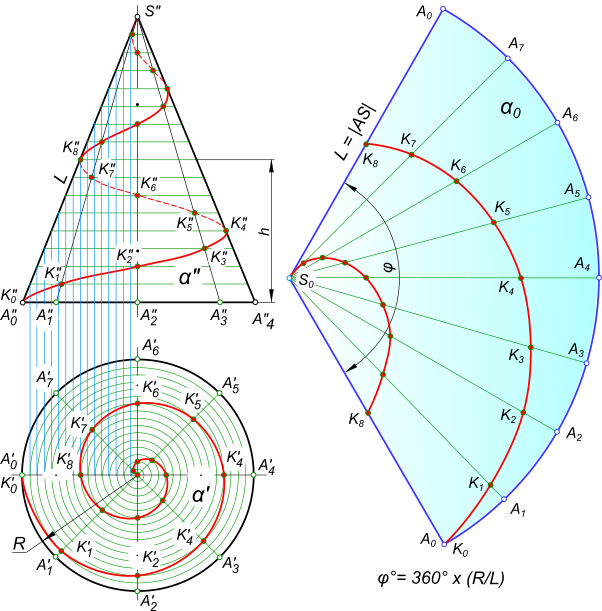
В этом случае, точка совершает равномерно-поступательное движение вдоль образующей прямого кругового конуса, а сама образующая SA вращается вокруг его оси с постоянной угловой скорости. Расстояние между точками смежных витков, измеренное параллельно оси конуса (например между точками AK8), является шагом h конической винтовой линии. Проекция винтовой линии на фронтальной плоскости проекций представляет собой синусоиду с затухающим колебанием (затухающей волной), а на горизонтальной — спираль Архимеда. При построении развертки боковой поверхности конуса винтовая линия развернется в спираль, а конус — в сектор, угол при вершине которого равен φ= 360°×(h/L), а длина дуги радиуса R, соответствующая углу φ, равна 2πR.
Методики расчета
По сопротивлению
Давайте разберемся как рассчитать длину нихромовой проволоки по мощности и сопротивлению. Расчёт начинается с определения требуемой мощности. Представим, что, нам нужна нить из нихрома для паяльника малых размеров мощностью в 10 Ватт, который будет работать от блока питания на 12В. Для этого у нас есть проволока диаметром 0.12 мм.

Простейший расчет длины нихрома по мощности без учета нагрева выполняется так:
Определим силу тока:
P=UI
I=P/U=10/12=0,83 A
Расчет сопротивления нихромовой проволоки проводим по закону Ома:
R=U/I=12/0,83=14,5 Ома
Длина проволоки равна:
l=SR/ρ,
где S – площадь поперечного сечения, ρ – удельное сопротивление.
Или по такой формуле:
l= (Rπd2)/4ρ
Но сначала нужно рассчитать удельное сопротивление для нихромовой проволоки диаметром 0.12мм. Оно зависит от диаметра – чем он больше, тем меньше сопротивление.
L=(14.5*3,14*0.12^2)/4*1,1=0,149м=14,9см
Тоже самое можно взять из ГОСТ 12766.1-90 табл. 8, где указана величина в 95.6 Ом/м, если по ней пересчитать, то получится почти тоже самое:
L=Rтреб/Rтабл=14,4/95,6=0,151м=15,1см
Для нагревателя мощностью 10 ватт, который питается от 12В, нужно 15.1см.
Если вам нужно выполнить расчет числа витков спирали, чтобы её свить из нихромовой проволоки такой длины, то используйте следующие формулы:
Длина одного витка:
l1=π(D+d/2),
Количество витков:
N=L/(π(D+d/2)),
где L и d – длина и диаметр проволоки, D – диаметр стержня на котором будут мотать спираль.
Допустим мы будем мотать нихромовую проволоку на стержень диаметром 3 мм, тогда расчеты проводим в миллиметрах:
N=151/(3,14(3+0,12/2))=15,71 витков
Но при этом нужно учитывать, способен ли вообще нихром такого сечения выдержать этот ток. Подробные таблицы для определения максимального допустимого тока при определенной температуре для конкретных сечений приведены ниже. Простыми словами – вы определяете, до скольки градусов должна греться проволока и выбираете её сечение для расчётного тока.
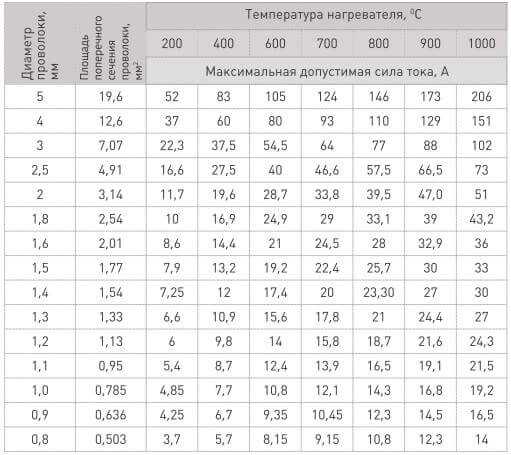
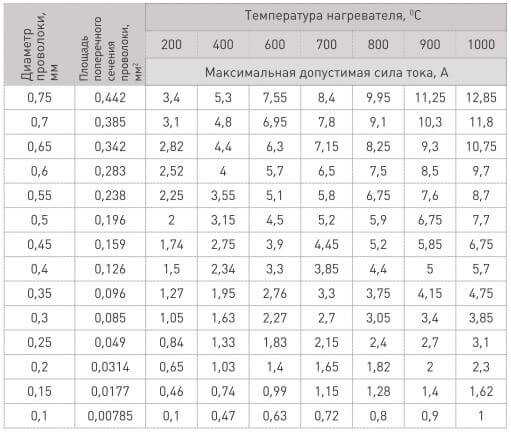
Также учтите, что если нагреватель находится внутри жидкости, то ток можно увеличить в 1.2-1.5 раз, а если в замкнутом пространстве, то наоборот – уменьшить.
По температуре
Проблема приведенного выше расчёта в том, что мы считаем сопротивление холодной спирали по диаметру нихромовой нити и её длине. Но оно зависит от температуры, при этом же нужно учитывать при каких условиях получится её достичь. Если для резки пенопласта или для обогревателя такой расчет еще применим, то для муфельной печи он будет слишком грубым.

Приведем пример расчетов нихрома для печи.
Сначала определяют её объём, допустим 50 литров, далее определяют мощность, для этого есть эмпирическое правило:
- до 50 литров – 100Вт/л;
- 100-500 литров – 50-70 Вт/л.
Тогда в нашем случае:
P=Pэмп*V=50*100=5 кВт.
Дальше считаем силу тока и сопротивление:
Для 220В:
I=5000/220=22.7 Ампера
R=220/22.7=9,7 Ом
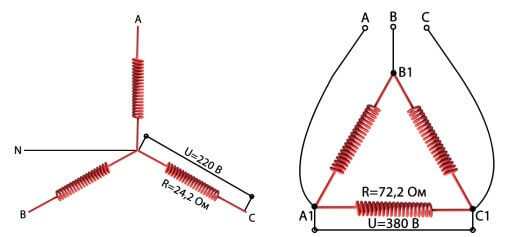
Для 380В при подключении спиралей звездой, расчет будет следующим.
Делим мощность на 3 фазы:
Pф=5/3=1,66 кВт на фазу
При подключении звездой, к каждой ветви прикладывается 220В (фазное напряжение, может отличаться в зависимости от вашей электроустановки), тогда ток:
I=1660/220=7.54 А
Сопротивление:
R=220/7.54=29.1 Ом
Для соединения треугольником рассчитываем по линейному напряжению 380В:
I=1660/380=4.36 А
R=380/4.36=87.1 Ом
Для определения диаметра учитывают удельную поверхностную мощность нагревателя. Рассчитаем длину, удельные сопротивления берем с табл. 8. ГОСТ 12766.1-90, но прежде определим диаметр.
Для расчета удельной поверхностной мощности печи используют формулу.
Bэф (зависит от теплопринимающей поверхности) и a (коэф. Эффективности излучения) – выбираются по следующим таблицам.
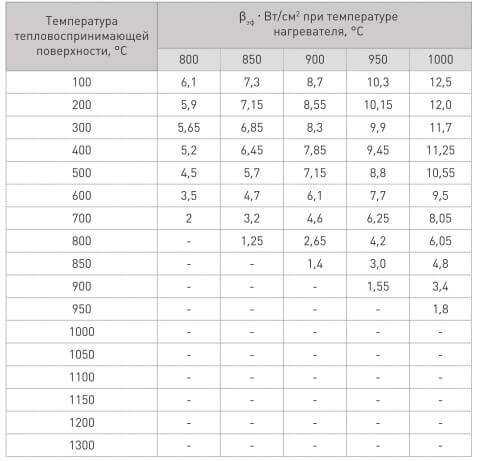
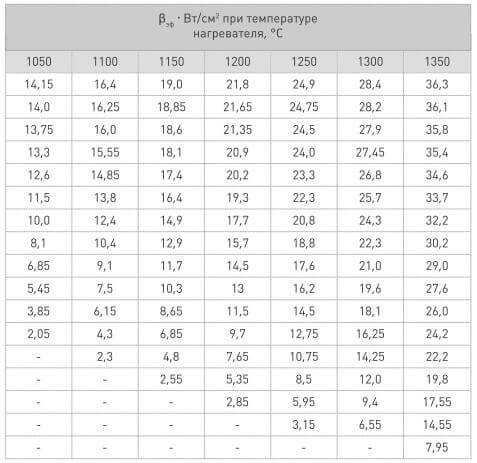
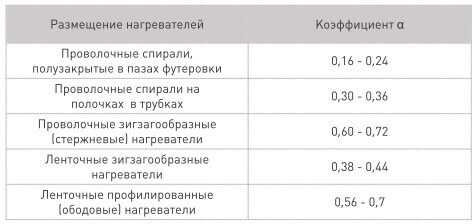
Итак, для нагрева печи до 1000 градусов, возьмём температуру спирали в 1100 градусов, тогда по таблице подбора Вэф выбираем значение в 4,3 Вт/см2, а по таблице подбора коэффициента а – 0,2.
Вдоп=Вэф*а=4,3*0.2= 0,86 Вт/см2 =0.86*10^4 Вт/м2
Диаметр определяют по формуле:
рт – удельное сопротивление материала нагревателя при заданной t, определяется по ГОСТ 12766.1, таблица 9 (приведена ниже).

Для нихрома Х80Н20 – 1,025
рт=р20*р1000=1.13*10^6*1.025=1.15*10^6 Ом/мм
Тогда для подключения к трёхфазной сети по схеме «Звезда»:
d=1,23 мм
Длина рассчитывается по формуле:
L=42м
Проверим значения:
L=R/(p*k)=29.1/(0.82*1.033)=34м
Значения отличаются из-за высокой температуры спирали, проверка не учитывает ряда факторов. Поэтому примем за длину 1 спирали – 42м, тогда для трёх спиралей нужно 126 метров нихрома 1,3 мм.
Примеры использования коэффициента роста спирали
Коэффициент роста спирали широко применяется в различных областях, где необходимо оценивать процентное изменение каких-либо параметров во времени или пространстве. Рассмотрим несколько примеров использования данного коэффициента:
1. Финансовая аналитика
Коэффициент роста спирали часто используется в финансовой аналитике для оценки темпов и направления развития компаний или рынков. Например, с помощью данного коэффициента можно выявить динамику роста объема продаж или прибыли в определенный период времени. Это позволяет инвесторам и аналитикам прогнозировать дальнейшее развитие и решать вопросы инвестирования.
2. Демографические исследования
В демографических исследованиях коэффициент роста спирали помогает изучать динамику изменения численности населения. Например, с его помощью можно определить темпы роста или снижения населения на определенной территории и прогнозировать возможные демографические изменения в будущем.
3. Маркетинговые исследования
В маркетинговых исследованиях коэффициент роста спирали используется для анализа и прогнозирования тенденций спроса на товары или услуги. Он позволяет оценить динамику изменения популярности или покупательского спроса на определенный товар или услугу и принять решения по маркетинговой стратегии.
4. Экологические исследования
Коэффициент роста спирали может быть также использован в экологических исследованиях для оценки изменений в биологических популяциях. С его помощью можно изучать динамику популяций животных или растений, а также прогнозировать возможные сдвиги в экосистемах при изменении условий среды.
5. Географический анализ
В географическом анализе коэффициент роста спирали может быть использован для изучения темпов развития и изменения ландшафта. Например, с его помощью можно оценить темпы эрозии почвы или изменения лесного покрова и принять меры по сохранению природных ресурсов.
6. Технический анализ на бирже
В техническом анализе на финансовом рынке коэффициент роста спирали может быть использован для оценки динамики изменения цен на активы или индексы. С его помощью можно определить направление и силу тренда на рынке и принять решения по торговле акциями или другими финансовыми инструментами.
7. Медицинская статистика
В медицинской статистике коэффициент роста спирали может быть использован для оценки изменений в заболеваемости или смертности от определенных заболеваний. С его помощью можно определить темпы распространения эпидемий или возможные риски для здоровья населения.
Это лишь некоторые примеры использования коэффициента роста спирали, который является универсальным инструментом для анализа динамики и прогнозирования изменений в различных областях.
Расчет спирали
Расчет неизвестных размеров спирали по известным размерам. Параметры спирали: внешний диаметр, внутренний диаметр, толщина (шаг спирали), длина спирали, число витков.
Данный калькулятор позволяет рассчитать неизвестные параметры спирали по известным параметрам.

Есть пять параметров спирали: внешний диаметр — D, внутренний диаметр — d, толщина (шаг спирали) — t, длина спирали — L, число витков — n. Есть уравнения, устанавливающие связь между этими параметрами (формулы приведены под калькулятором). По этим уравнениям, зная какие-либо три параметра, можно вычислить два оставшихся неизвестных параметра.
Где мы встречаемся со спиралью? Чаще всего при покупке каких-либо материалов в рулонах, будь то рулоны обоев или рулоны туалетной бумаги. Используя калькулятор ниже, можно рассчитать, например, количество погонных метров в рулоне т.е. длину спирали, зная или измерив толщину материала или посчитав количество витков, и измерив внутренний и внешний диаметры рулона. Калькулятор также может решать и обратные задачи , например, по длине спирали и её диаметрам найти толщину и количество витков спирали. Теория и формулы, как обычно, приведены под калькулятором.
При вводе известных параметров проверяйте правильно ли указана размерность для введенных значений. 20 метров это не тоже самое что 20 миллиметров.
Расчет спирали
Точность вычисления
Знаков после запятой: 4
Рассчитать
Внутренний диаметр
Внешний диаметр
Число витков Ссылка Сохранить Виджет
Архимедова спираль
Под Архимедовой спиралью понимают плоскую кривую (спираль), которая отображает траекторию точки М, равномерно движущейся вдоль луча ОА, в то время как сам луч равномерно вращается вокруг точки О.

Если обозначить расстояние от О до М как ρ, а угол поворота луча как φ, то в полярных координатах зависимость расстояния вдоль луча от угла поворота луча можно записать как
где k это параметр спирали, соответствующий величине смещения точки вдоль луча при повороте на один радиан. Повороту на 2π будет соответствовать смещение на 2πk.
Так как 2π это полный оборот, число a, также называемое шагом спирали, будет соответствовать расстоянию между двумя соседними витками спирали и начальное уравнение можно переписать в виде.
Так как шаг спирали постоянный, то чем дальше от центра, тем больше витки спирали по форме напоминают окружность. К слову, если движение точки описывается другим уравнением, то это какая-то другая спираль.
Для того, чтобы вывести формулу вычисления длины спирали, рассмотрим бесконечно малое приращение длины.
Бесконечно малый отрезок дуги dl можно представить как гипотенузу прямоугольного треугольника с катетами dρ и dh. По теореме Пифагора гипотенуза равна
Бесконечно малый отрезок dh можно заменить на бесконечно малую часть дуги окружности с радиусом ρ, длина которой ρdφ.
Из уравнения спирали заменяем ρ на kφ, и dρ на kdφ
Таким образом мы получили зависимость dl от dφ. Чтобы найти длину L достаточно взять интеграл от начального угла поворота луча до конечного угла поворота луча.
Интеграл я выводить не буду, его уже вывели до меня. Конечный результат
В случае если спираль выходит из точки О, то есть начальный угол поворота луча равен 0, формула упрощается
Если мы говорим о рулоне, то там скорее всего начальный угол все же не равен нулю, то есть есть ненулевой внутренний диаметр (например, там есть втулка). Как же перейти от углов к диаметрам, и найти число витков спирали?
Число витков спирали связано с углами следующим очевидным соотношением:
Диаметры можно связать с углом непосредственно по уравнению спирали (если вспомнить что диаметр это два радиуса)
Эти соотношения и используются для нахождения неизвестных параметров спирали по известным. Осталось только заметить, что уравнение длины является трансцендентным, и решение обратной задачи — по известной длине найти что-то неизвестное, невозможно найти аналитически. Для получения решения приходится прибегать к численным методам, в частности, в калькуляторе выше используется метод секущих.
Коротко о главном
Итак, как было сказано ранее, можно купить готовые спирали, которые рассчитаны на определенное сопротивление и подходят для определенных моделей электронок.
Однако, переходя на этап профессионального вейпинга, многие парильщики изъявляют желание наматывать испарители своих электронных собственными силами, что дает массу преимуществ:
Расчет сопротивления: зачем и как правильно провести?
Обычно проблемы легко исправляются. Проверьте положение катушек, чтобы убедиться, что он не касается колоды или столбов. Убедитесь, что ваш распылитель полностью завинчен в считыватель омов. Если эти шаги исправили вашу проблему, вы готовы перейти к следующему шагу. Если эти шаги не исправили вашу проблему, попробуйте сделать еще одну катушку. Если у вас по-прежнему возникает проблема, может возникнуть проблема с вашим распылителем или с вашим считывателем омов.
Испытание на обмотку катушки и устранение горячих точек
Как только ваши катушки начнут светиться, прекратите стрелять в ваш мод и аккуратно сжать свою катушку вместе с пинцетом. Повторяйте этот процесс до тех пор, пока катушка не будет равномерно светиться, начиная с центра, движущегося к внешним оберткам.
-
Экономия.
Если говорить о долгосрочной самостоятельной намотке атомайзера, то речь идет о колоссальной экономии. Готовые спирали стоят практически столько же, сколько обойдется целый моток канталовой или нихромовой проволоки, из которой можно скрутить как минимум десяток вкусных койлов. -
Уровень мастерства.
Это, пожалуй, то, ради чего вейперы и придумывают всевозможными сэтапы для своих модов. Каждый, кто занимается намоткой атомайзера, пытается придумать что-то новенькое, чтоб показать свой уровень профессионализма в этой поистине увлекательной культуре. -
Достижение определенных показателей вейпа.
К примеру, односпиральный обслуживаемый атомайзер можно намотать таким образом, что он будет выдавать вдвое больше пара, нежели его более современный собрат. Да-да, все это благодаря удачно подобранной намотке. Тогда как готовые спирали рассчитаны только на определенные показатели сопротивления.
Что помогает определить калькулятор?
Есть много вещей, которые вы можете использовать для фитиля вашей катушки, органического хлопка, кремнистого фитиля, эко-шерсти, все очень популярны по разным причинам и использованию. Для этой цели мы предпочитаем органический хлопок для его превосходных вкусовых и капиллярных способностей. Вам понадобится кусок материала, достаточно большой, чтобы плотно вписаться в вашу катушку, оставляя примерно половину дюйма с каждой стороны. Иногда это помогает мокрой и скручивать конец фитиля, чтобы начать.
Итоги
Онлайн калькулятор для расчета спирали поможет вам с быстрыми предварительными расчетами, но для точного учета всех особенностей даже второго метода расчета с учетом температуры может быть не достаточно
На практике существует еще очень много факторов, которые нужно взять во внимание при расчете параметров нагревателя
Если вам нужна помощь с расчетами нагревателей – обращайтесь к нам. Наши специалисты имеют огромный опыт в проектировании нагревательных элементов для различного промышленного оборудования. Мы поможем с расчетами оптимальных параметров нагревательных элементов для вашего оборудования и можем изготовить любой тип нагревателей для Вас.
Источник статьи: http://polymernagrev.ru/nagrev-v-proizvodstve/kalkulyator-rascheta-spirali-iz-nikhroma-i-fekhralya-dlya-nagrevateley/





























