В призму вписан цилиндр найти площадь боковой поверхности цилиндра

Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.

Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

Правильной четырёхугольной призмой – называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками. Площадь боковой поверхности данной призмы – это площадь 4-х равных прямоугольников. Длина прямоугольника равна диаметру цилиндра, ширина прямоугольника равна высоте цилиндра.

Найдём площадь боковой поверхности призмы:

S_{бок. поверх.} = 4·S_{прямоугольника} = 4· h ·( r + r ) = 4·3·(3 + 3) = 4·3·6 = 72

Уроки арифметики на русском языке

Урок №2. Сложение натуральных чисел
Урок №3. Вычитание натуральных чисел
Урок №4. Таблица умножения
Урок №5. Умножение натуральных чисел
Урок №6. Деление натуральных чисел
Урок №8. Величины и их измерение
Урок №10. Делимость чисел
Урок №13. Обыкновенные дроби
Урок №15. Сложение дробей
Урок №16. Вычитание дробей
Урок №17. Умножение дробей
Урок №18. Деление дробей
Урок №21. Конечные десятичные дроби
Урок №22. Сложение десятичных дробей
Урок №23. Вычитание десятичных дробей
Урок №24. Умножение десятичных дробей
Урок №25. Деление десятичных дробей
Урок №26. Округление чисел
Урок №1. Отношение величин
Урок №2. Пропорции
Урок №6. Проценты
Урок №7. Нахождение процентов данного числа
Урок №12. Среднее арифметическое
Урок №14. Масштаб

Цилиндр вписан в правильную треугольную призму найдите площадь поверхности цилиндра

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

В куб вписан шар радиуса 1. Найдите объем куба.

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на

Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на

Около куба с ребром описан шар. Найдите объем этого шара, деленный на

Вершина A куба с ребром 1,6 является центром сферы, проходящей через точку A₁. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра

Определение 1. Цилиндром, вписанным в призму, называют такой , окружности которого вписаны в , являющиеся , а (рис. 1).

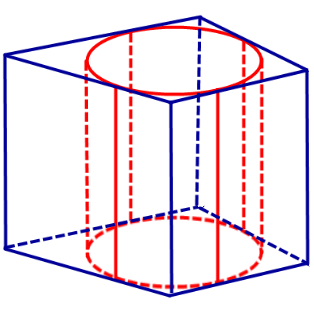
Рис.1

Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.

Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.

Утверждение 1. Если в можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен

Доказательство. Рассмотрим призму A₁A₂ … A_nA’₁A’₂ … A’_n, у которой в A₁A₂ … A_n и A’₁A’₂ … A’_n можно вписать окружности. Пусть в нижнее A₁A₂ … A_n призмы A₁A₂ … A_nA’₁A’₂ … A’_n вписана окружность с центром O радиуса r, которая касается прямой A₁A₂ в точке K . Проведем через точку O прямую, параллельную A₁A’₁ призмы и пересекающую плоскость верхнего в точке O’ (рис. 2).

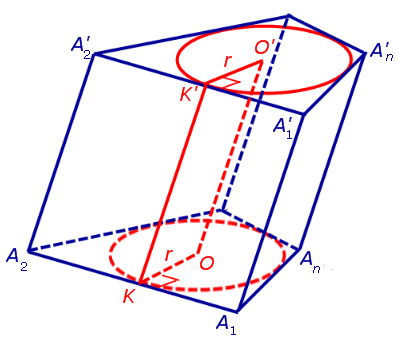
Рис.2

Вследствие плоскость KOO’ параллелельна боковому ребру A₁A’₁ , а ее линия пересечения KK’ с боковой гранью призмы A₁A₂A’₁A’₂ Замечая, что отрезки OK и O’K’ , заключаем, что четырехугольник OO’K’K – .

Поскольку OK – это радиус окружности, проведенный в точку касания окружности радиуса r с центром O и прямой A₁A₂ , то . Значит, и O’K’ = r и угол O’K’A’₁ равен 90°, то есть

Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’₁A’₂, A’₂A’₃, … , A_{n – 1}A_n, а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’₁A’₂ … A’_n окружности.

В силу того, что прямые OO’ и A₁A’₁ параллельны по построению, а прямые OA₁ и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A₁A’₁ является , откуда вытекает равенство: OO’ = A₁A’₁.

Утверждение 1 доказано.

Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:

Призма является ;
В основания призмы можно вписать окружности.

Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.

С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).

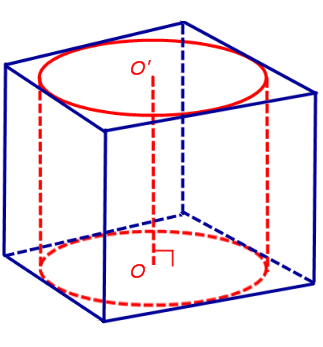
Рис.3

Согласно отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.

Теперь рассмотрим h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.

Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).

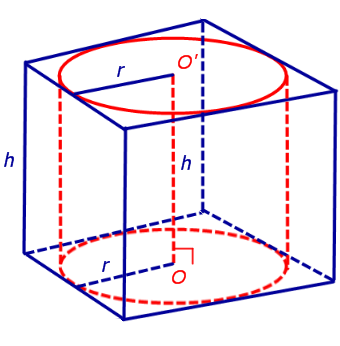
Рис.4

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Цилиндр с осью OO’, радиусом r и высотой h и будет вписан в исходную призму.

Доказательство теоремы завершено.

Следствие 1 . , описанной около цилиндра, равна

Следствие 2. В любую можно вписать цилиндр.

Справедливость этого утверждения вытекает из того факта, что

Следствие 3. В любую можно вписать цилиндр.

Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.

Уроки арифметики на українській мові

Урок №2. Додавання натуральних чисел
Урок №3. Віднімання натуральних чисел
Урок №4. Таблиця множення
Урок №5. Множення натуральних чисел
Урок №6. Ділення натуральних чисел
Урок №8. Величини та їх вимірювання
Урок №10. Подільність чисел
Урок №13. Звичайні дроби
Урок №15. Додавання дробів
Урок №16. Віднімання дробів
Урок №17. Множення дробів
Урок №18. Ділення дробів
Урок №21. Кінечни десяткові дроби
Урок №22. Додавання десяткових дробів
Урок №23. Віднимання десяткових дробів
Урок №24. Множення десяткових дробів
Урок №25. Ділення десяткових дробів
Урок №18. Нескінченний десятковий дріб
Урок №19. Відношення величин
Урок №20. Пропорції
Урок №6. Відсотки
Урок №7. Відсотки (2)
Урок №12. Середнє арифметичне
Урок №14. Масштаб

Заключение

На уроке мы разобрали комбинации призмы и цилиндра, а также решили задачи по темам: цилиндр, описанный вокруг призмы и цилиндр, вписанный в призму.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/11-klass/btela-vraweniya-b/kombinatsiya-prizmy-i-tsilindra

https://www.youtube.com/watch?v=W5LLg5EJJqI

https://www.youtube.com/watch?v=jfZ6B4hvkjY

http://www.yaklass.ru/p/geometria/11-klass/tela-vrashcheniia-10442/tcilindr-9260/re-04ed80b8-bfe5-4f48-b571-3e5278f08ea8

http://схемо.рф/upload/sx/470/preview/8.jpg

http://1.bp.blogspot.com/-9N8xpfP3SOw/T1TOzXinW2I/AAAAAAAAA9Q/fEXKxGBY99I/s1600/Geom_1.jpg

http://cs405725.vk.me/v405725468/6209/cEdhWBPmpNQ.jpg

https://yandex.ru/images/search?p=4&text=%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8%20%D0%BD%D0%B0%20%D0%BA%D0%BE%D0%BC%D0%B1%D0%B8%D0%BD%D0%B0%D1%86%D0%B8%D1%8E%20%D1%86%D0%B8%D0%BB%D0%B8%D0%BD%D0%B4%D1%80%D0%B0%20%D0%B8%20%D0%BF%D1%80%D0%B8%D0%B7%D0%BC%D1%8B&img_url=http%3A%2F%2Fuslide.ru%2Fimages%2F12%2F18580%2F960%2Fimg6.jpg&pos=121&rpt=simage&_=1450898849842