Как найти диаметр основания цилиндра при известной площади боковой поверхности и высоте

Объем цилиндра

Shпиr

Спасибо, очень полезным оказался

Спасибо, очень удобный калькулятор. Вспомнила формулу вычисления объёма. Невозможно держать в голове всю школьную программу. Пользуешься только необходимыми вычислениями, которые нужны для моей профессии.

А в каких единицах измерения, в бананах или коровах? Услугами данного калькулятора пользуются не профессора! Бесполезно потраченное время!

Оксана, результат у тебя, и таких как ты, получится в кубических курах. Потому, что у вас мозги куриные!

В школу ходить надо было. Если измерение проводится в см, то и получаете см возведённые в куб.

Учитель не до конца вам объяснил или вы не усвоили, что в геометрии как правило объем измеряется в кубах, соответственно:

— Если вводите в бананах, то результат будет в бананах кубических, — Если в сантиметрах, то результат будет в сантиметрах кубических (см³). и т.д.

Слушайте учителей, образовывайтесь, заставляйте свой мозг работать.

Не нужно быть профессором чтобы воспользоваться этим калькулятором Разницы нету метры, сантимеры, миллиметры он вам выдаёт куб того что вы ввели.

📏 Как работает калькулятор объема цилиндра?

Калькулятор объема цилиндра работает на основе математической формулы для расчета объема цилиндра, рассмотренной выше.

Чтобы рассчитать объем цилиндра, пользователь должен ввести значения радиуса основания и высоты цилиндра в соответствующие поля калькулятора и нажать кнопку «Рассчитать». Калькулятор использует введенные значения, выполняет математическую операцию по формуле и выводит результат в соответствующем поле на экране.

Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения (например, сантиметры или дюймы) и возможность рассчитать объем цилиндра, используя диаметр основания вместо радиуса.

Понятие цилиндра

Сейчас мы говорим про мужской головной убор, который был популярен в 19 веке и стал достаточно узнаваем в массовой культуре. Оказывается, в математике также существует цилиндр. И они похожи по форме.

Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон. 

Возможно, для уточнения некоторых терминов вам захочется заглянуть в статью «Тела вращения». 

Если посмотреть на форму шляпы, то она действительно будет похожа на геометрическую фигуру.  Встретить цилиндр можно и в наше время. Обычная кружка является цилиндром.

Прямая, вокруг которой мы крутили прямоугольник, чтобы получить цилиндр, — это ось цилиндра. 

Также, как у Земли есть ось вращения, она есть и у цилиндра. 

Наша кружка стоит на круглом дне. Это дно, как и самый верх кружки, будут называться основаниями цилиндра. 

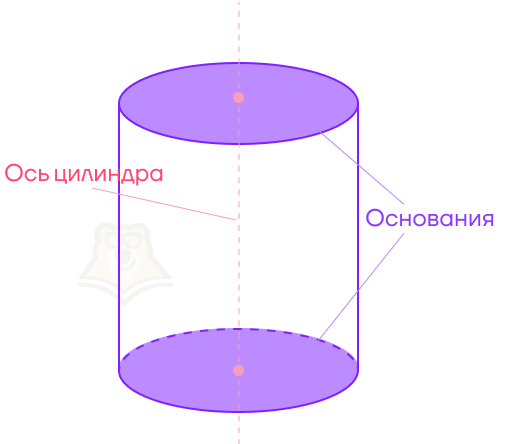
Снова посмотрим на стенки кружки. В цилиндре эта поверхность будет называться цилиндрической поверхностью. Ее также могут называть боковой поверхностью цилиндра. 

Представим, что наша кружка раскрашена вертикальными линиями. Эти линии будут лежать на цилиндрической поверхности и перпендикулярны основаниям. У них есть название:

Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований. 

Все образующие, — а в цилиндре их очень-очень много, —лежат только на цилиндрической поверхности. Эта поверхность и состоит из множества образующих. 

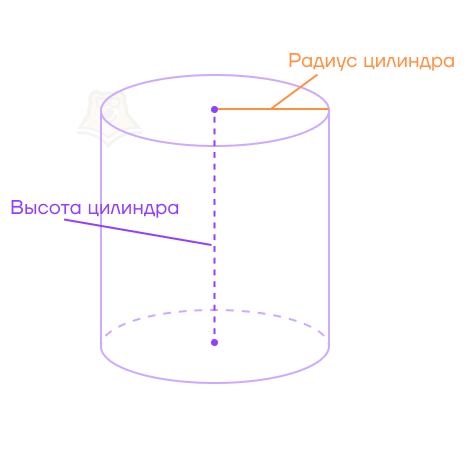
Узнаем ширину кружки. Для этого нужно измерить радиус дна. Этот же радиус будет радиусом основания, а в цилиндре он называется радиусом цилиндра. 

Теперь найдем высоту кружки. Для этого нужно измерить расстояние от дна до самого верха кружки. 

В математике это будет расстоянием между плоскостями, а ищется оно как длина перпендикуляра, опущенного из одной плоскости на другую. Подробнее про это можно прочесть в статье «Расстояния между фигурами». 

Высота цилиндра — перпендикуляр, опущенный из плоскости одного основания на плоскость второго основания. 

Поиск радиуса основания цилиндра

Радиус основания цилиндра можно найти, зная площадь его боковой поверхности и высоту. Для этого следует использовать следующую формулу:

Радиус = √(Площадь боковой поверхности / (2π * Высота))

Где:

• Радиус — радиус основания цилиндра
• Площадь боковой поверхности — площадь поверхности, ограниченной боковой поверхностью цилиндра
• Высота — высота цилиндра
• π — математическая константа, примерное значение которой равно 3.14159

Пример нахождения радиуса основания цилиндра:

1. Известно, что площадь боковой поверхности равна 150 квадратных сантиметров и высота равна 10 сантиметров.
2. Подставляем известные значения в формулу: Радиус = √(150 / (2π * 10))
3. Выполняем вычисления: Радиус ≈ √(150 / (2 * 3.14159 * 10)) ≈ √(150 / 62.8318) ≈ √(2.3872) ≈ 1.5449
4. Ответ: Радиус основания цилиндра равен примерно 1.5449 сантиметра

Таким образом, зная площадь боковой поверхности и высоту цилиндра, можно вычислить радиус его основания с использованием формулы, описанной выше. Этот результат будет полезен, например, при построении цилиндра или решении практических задач, связанных с данным геометрическим телом.

Связь между радиусом и диаметром

Если нам известен диаметр окружности, то мы можем найти радиус, разделив его на 2: R = D/2. В свою очередь, зная радиус, мы можем найти диаметр, умножив его на 2: D = 2R.

В случае, если мы знаем высоту и площадь боковой поверхности цилиндра, мы можем использовать формулы для нахождения радиуса или диаметра основания. Диаметр основания можно найти, используя формулу: D = 2√(S/πh), где S — площадь боковой поверхности, а h — высота цилиндра. Зная диаметр основания, мы также можем найти радиус, разделив его на 2: R = D/2.

Таким образом, радиус и диаметр имеют прямую зависимость друг от друга: удвоенный радиус равен диаметру, а диаметр можно найти, зная радиус, или наоборот, радиус можно найти, зная диаметр. Эти характеристики помогают нам определить размеры и свойства геометрических фигур.

Расчет радиуса основания по площади боковой поверхности

Площадь боковой поверхности боковой поверхности цилиндра вычисляется по формуле:

S_бок = 2πrh,

где S_бок — площадь боковой поверхности цилиндра, r — радиус основания, h — высота цилиндра.

Чтобы найти радиус основания по площади боковой поверхности, нужно решить уравнение относительно r:

S_бок = 2πrh,

Разделим обе части уравнения на 2πh:

r = S_бок / (2πh).

Таким образом, радиус основания цилиндра можно найти, разделив площадь боковой поверхности на произведение числа π на двойное произведение радиуса и высоты.

Для наглядности, представим расчет в виде таблицы:

Шаг	Действие	Формула	Результат
1	Вставьте данные	—	—
2	Вычислите r	r = Sбок / (2πh)	—

Используйте данную формулу и шаги таблицы для расчета радиуса основания цилиндра по известной площади боковой поверхности и высоте.

Как использовать калькулятор объема цилиндра?

Онлайн-калькулятор объема цилиндра разработан для быстрого и точного расчета объема различных цилиндрических объектов. Давайте разберемся, как им пользоваться:

1. Откройте калькулятор на сайте.

2. Введите радиус основания цилиндра в соответствующее поле.

3. Введите высоту цилиндра.

4. Если вы хотите получить результат в литрах, выберите соответствующую единицу измерения.

5. Нажмите кнопку «Рассчитать».

6. Результат появится ниже, отображая объем цилиндра в выбранной вами единице измерения.

7. При необходимости вы можете изменить введенные значения и повторить расчет.

Виды цилиндров

1. Прямой цилиндр – имеет одинаковые симметричные основания (круг или эллипс), параллельные друг другу. Отрезок между точками симметрии оснований перпендикулярен им, является осью симметрии и высотой фигуры.
2. Наклонный цилиндр – имеет одинаковые симметричные и параллельные друг другу основания. Но отрезок между точками симметрии не перпендикулярен этим основаниям.
3. Косой (скошенный) цилиндр – основания фигуры не взаимно параллельны.
4. Круговой цилиндр – основаниями является круг. Также выделяют эллиптические, параболические и гиперболические цилиндры.
5. Равносторонний цилиндр – прямой круговой цилиндр, диаметр основания которого равен его высоте.

Сами прямые называют образующими цилиндрической поверхности.
Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.

Так как все образующие и ось перпендикулярны плоскости альфа, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).

Если построить ещё одну плоскость бета, которая будет параллельна плоскости альфа, то отрезки образующих, заключённые между плоскостями альфа и бета будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости бета, дают окружность, равную окружности, лежащей в плоскости альфа.

Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях альфа и бета) называется цилиндром.
Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.

Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.

Сечения цилиндра различными плоскостями

Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого – образующие, а две другие – отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).

Основные формулы

Формула для вычисления площади боковой поверхности цилиндра: Sбок=2пRL.

То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: Sполн=2пR(R+L).

Примеры и разбор решения заданий тренировочного модуля

Дан цилиндр.

Выберите значение площади его боковой поверхности

1. 60π
2. 192π
3. 120π
4. 36π

Решение:

Площадь боковой поверхности вычисляется по формуле: S=2πRL.

R=6, L=10

Подставим: S=2π·6·10=120π.

Ответ: 3) 120π

Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.

Решение:

Sполн=2πR(R+L)

По условию задачи L=R+6.

144π=2πR(R+R+6).

Получили квадратное уравнение относительно радиуса:

R2+6R-72=0

R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.

Ответ: 12.

Задача

Осевое сечение цилиндра – квадрат со стороной 20 см. Найти высоту цилиндра, радиус цилиндра, ось цилиндра и площадь основания цилиндра.

Решение

Одна из сторон осевого сечения – образующая (она же равна оси цилиндра и она же равна высоте). Значит, высота и ось равны 20 см. Далее, вторая сторона осевого сечения – диаметр основания. Он равен 20 см, значит, радиус – 10 см. Наконец, площадь основания ищется по формуле

Итак, ребята, на этом уроке мы изучили, что такое цилиндрическая поверхность, её образующая; цилиндр, все его элементы и сечения; площади поверхностей цилиндра.

Как работает онлайн-калькулятор объема цилиндра

Сегодня многие задачи можно решить с помощью интернет-сервисов, и онлайн-калькулятор объема цилиндра – отличный пример. Чтобы правильно вычислить объем цилиндра, используется простая формула: V = π * r^2 * h, где π (пи) — математическая константа, приблизительно равная 3,14, r — радиус основания цилиндра, а h — его высота.

1. Ввод данных: В первую очередь, пользователь должен внести необходимые параметры: диаметр (или радиус) и высоту цилиндра. Эти параметры могут быть представлены в различных единицах измерения: метрах, сантиметрах или миллиметрах.
2. Обработка информации: Как только данные введены, калькулятор автоматически применяет формулу для вычисления объема. Этот процесс занимает считанные миллисекунды.
3. Результат: Пользователь получает ответ в кубометрах, кубических сантиметрах или других единицах, в зависимости от исходных данных.

Преимущества использования онлайн-калькулятора

• Точность расчетов. Шанс ошибиться при ручном расчете гораздо выше, чем при использовании автоматизированной системы, особенно для тех, кто редко сталкивается с подобными вычислениями.
• Быстрота. Время, потраченное на ввод параметров и получение результата, составляет всего несколько секунд, в то время как ручной расчет может занять гораздо больше времени.
• Доступность. Необходимость рассчитать объем цилиндра может возникнуть в любом месте и в любое время. Благодаря онлайн-калькулятору это возможно даже через смартфон.
• Многозадачность. Большинство современных калькуляторов также предоставляют дополнительные функции, такие как вычисление площади поверхности цилиндра или его боковой поверхности.
• Образовательный аспект. Использование онлайн-калькулятора может быть полезным инструментом для студентов и школьников, изучающих математику, так как многие калькуляторы показывают детальные шаги расчета, помогая понять, как получен конечный результат.

Призма

Определения:

1. Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
2. Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
3. Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
4. Боковая поверхность – объединение боковых граней.
5. Полная поверхность – объединение оснований и боковой поверхности.
6. Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
7. Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
8. Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
9. Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
10. Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
11. Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства и формулы для призмы:

• Основания призмы являются равными многоугольниками.
• Боковые грани призмы являются параллелограммами.
• Боковые ребра призмы параллельны и равны.
• Объём призмы равен произведению её высоты на площадь основания:

где: Sосн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:

• Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A2B2C2D2E2).
• Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
• Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
• Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:

где: Sсеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA1или BB1 и так далее).

Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:

где: Pсеч – периметр перпендикулярного сечения, l – длина бокового ребра.

Виды призм в стереометрии:

• Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
• Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):

где: Pосн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = Sосн∙h = Sосн∙l.

Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:

Свойства правильной призмы:

1. Основания правильной призмы являются правильными многоугольниками.
2. Боковые грани правильной призмы являются равными прямоугольниками.
3. Боковые ребра правильной призмы равны между собой.
4. Правильная призма является прямой.

Применение в разных областях

Цилиндр, несмотря на свою простоту, имеет широкое применение в различных сферах деятельности:

• Строительство. Здесь цилиндрические формы используются во многих конструкциях, начиная от колонн зданий и заканчивая водонапорными башнями. При этом, зная объем, можно точно рассчитать количество необходимого материала, будь то бетон или вода в резервуаре.
• Машиностроение. Двигатели, в особенности поршневые, требуют точных вычислений цилиндрических деталей. Здесь важны не только объем, но и площадь поверхности для оптимального теплоотвода.
• Аграрная сфера. Цилиндрические емкости используются для хранения зерна, воды или силоса. Зная объем, можно рассчитать емкость хранения или количества загружаемого материала.
• Медицина. Цилиндрические формы находят свое применение в различных медицинских устройствах и инструментах, начиная от шприцев до больших аппаратов МРТ.