Что такое цилиндр: определение, элементы, виды, варианты сечения

Как найти высоту цилиндра

Рассмотрим варианты нахождения высоты фигуры, а также длины ее образующей (которая равна этой высоте).

Первым делом взглянем на формулу: \(V=\pi R^2\times H\), где V — объем цилиндра, R — радиус основания, H — высота фигуры.

Через эту формулу можем выразить высоту:

\(H=\frac V{\pi R^2}\)

Таким образом мы можем узнать H данного геометрического тела, если нам известен его объем и радиус. Если же вместо радиуса мы знаем диаметр, формула расчета будет выглядеть так:

\(H=\frac{4V}{D^2}\)

В случае, когда нам известен диаметр и площадь фигуры, мы так же можем найти высоту

Следует обратить внимание, что в зависимости от того, будет ли известна площадь боковой или полной поверхности, формула будет меняться

Для расчета S боковой поверхности (часть, ограниченная цилиндрической поверхностью) цилиндра мы используем формулу:

\(S=2\pi RH\)

выражаем H и получаем:

\(H=\frac S{2\pi R}\)

Если известна S полной поверхности (включает в себя площадь оснований фигуры), используем формулу:

\(S=2\pi R(H+R)=2\pi R\times H+2\pi R^2\)

выражаем H и получаем:

\(H=\frac{S-2\pi R^2}{2\pi R}\)

Для третьего способа нужно будет провести прямоугольное сечение, ширина которого должна будет совпадать с диаметрами оснований, а длина — с образующими цилиндра.

Таким образом, получается прямоугольный треугольник САВ. А так как высота равна образующей, мы можем вычислить ее по теореме Пифагора:

\(СВ^2=АС^2-АВ^2\)

\(H=СВ=\sqrt{АС^2-АВ^2}\)

Призма

Определения:

1. Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
2. Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
3. Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
4. Боковая поверхность – объединение боковых граней.
5. Полная поверхность – объединение оснований и боковой поверхности.
6. Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
7. Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
8. Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
9. Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
10. Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
11. Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства и формулы для призмы:

• Основания призмы являются равными многоугольниками.
• Боковые грани призмы являются параллелограммами.
• Боковые ребра призмы параллельны и равны.
• Объём призмы равен произведению её высоты на площадь основания:

где: Sосн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:

• Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A2B2C2D2E2).
• Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
• Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
• Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:

где: Sсеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA1или BB1 и так далее).

Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:

где: Pсеч – периметр перпендикулярного сечения, l – длина бокового ребра.

Виды призм в стереометрии:

• Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
• Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):

где: Pосн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = Sосн∙h = Sосн∙l.

Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:

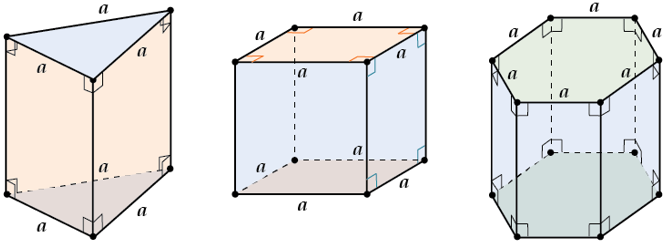
Свойства правильной призмы:

1. Основания правильной призмы являются правильными многоугольниками.
2. Боковые грани правильной призмы являются равными прямоугольниками.
3. Боковые ребра правильной призмы равны между собой.
4. Правильная призма является прямой.

1.1. Определение цилиндра

Рассмотрим
какую-либо линию (кривую, ломаную или смешанную) l, лежащую в некоторой
плокости α, и некоторую прямую S, пересекающую эту плоскость. Через все
точки данной линии l проведем прямые, параллельные прямой S; образованная этими
прямыми поверхность α называется цилиндрической поверхностью. Линия l
называется направляющей этой поверхности, прямые s1, s2,
s3,… − ее образующими.

Если направляющая
является ломаной, то такая цилиндрическая поверхность состоит из ряда плоских
полос, заключенных между парами параллельных прямых, и называется
призматической поверхностью. Образующие, проходящие через вершины направляющей
ломаной, называются ребрами призматической поверхности, плоские полосы между ними
− ее гранями.

Если рассечь
любую цилиндрическую поверхность произвольной плоскостью, не параллельной ее
образующим, то получим линию, которая также может быть принята за направляющую
данной поверхности. Среди направляющих выделяется та, которая, получается, от
сечения поверхности плоскостью, перпендикулярной образующим поверхности. Такое
сечение называется нормальным сечением, а соответствующая направляющая −
нормальной направляющей.

Если направляющая
− замкнутая (выпуклая) линия (ломаная или кривая), то соответствующая
поверхность называется замкнутой (выпуклой) призматической или цилиндрической
поверхностью. Из цилиндрических поверхностей простейшая имеет своей нормальной
направляющей окружность. Рассечем замкнутую выпуклую призматическую поверхность
двумя плоскостями, параллельными между собой, но не параллельными образующим.

В сечениях
получим выпуклые многоугольники. Теперь часть призматической поверхности,
заключенная между плоскостями α и α’, и две образовавшиеся при этом
многоугольные пластинки в этих плоскостях ограничивают тело, называемое
призматическим телом − призмой.

Цилиндрическое
тело − цилиндр определяется аналогично призме:
Цилиндром называется тело, ограниченное с боков замкнутой (выпуклой)
цилиндрической поверхностью, а с торцов двумя плоскими параллельными
основаниями. Оба основания цилиндра равны, также равны между собой и все
образующие цилиндра, т.е. отрезки образующих цилиндрической поверхности между
плоскостями оснований.

Цилиндром
(точнее, круговым цилиндром) называется  геометрическое тело, которое состоит
из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным
переносом, и всех отрезков, соединяющих соответствующие точки этих кругов (рис.
1).

Рис. 1 −
Цилиндр

Круги называются
основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей
кругов, − образующими цилиндра.

Так как
параллельный перенос есть движение, то основания цилиндра равны.

Так как при
параллельном переносе плоскость переходит в параллельную плоскость (или в
себя), то у цилиндра основания лежат в параллельных плоскостях.

Так как при
параллельном переносе точки смещаются по параллельным (или совпадающим) прямым
на одно и то же расстояние, то у цилиндра образующие параллельны и равны.

Поверхность
цилиндра состоит из оснований и боковой поверхности. Боковая поверхность
составлена из образующих.

Цилиндр называется
прямым, если его образующие перпендикулярны плоскостям оснований.

Прямой цилиндр
наглядно можно представить себе как геометрическое тело, которое описывает
прямоугольник при вращении его около стороны как оси (рис. 2).

Рис. 2 −
Прямой цилиндр

В дальнейшем мы
будем рассматривать только прямой цилиндр, называя его для краткости просто
цилиндром. 

Радиусом цилиндра
называется радиус его основания. Высотой цилиндра называется расстояние между
плоскостями его оснований. Осью цилиндра называется прямая, проходящая через
центры оснований. Она параллельна образующим.

Цилиндр
называется равносторонним, если
его высота равна диаметру основания.

Если основания
цилиндра плоские (и, следовательно, содержащие их плоскости параллельны), то
цилиндр называют стоящим на плоскости. Если основания стоящего на плоскости
цилиндра перпендикулярны образующей, то цилиндр называется прямым.

В частности, если
основание стоящего на плоскости цилиндра − круг, то говорят о круговом (круглом)
цилиндре; если эллипс − то эллиптическом.

Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся

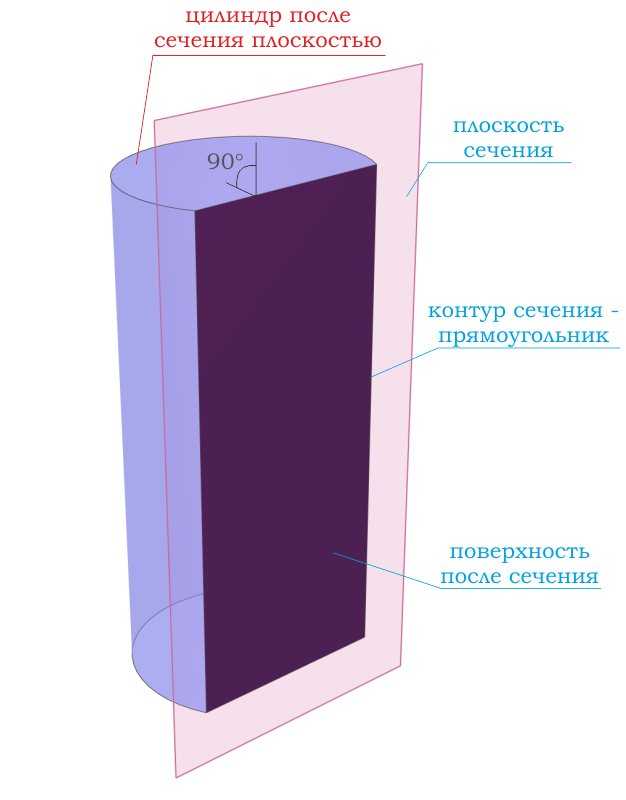
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура,

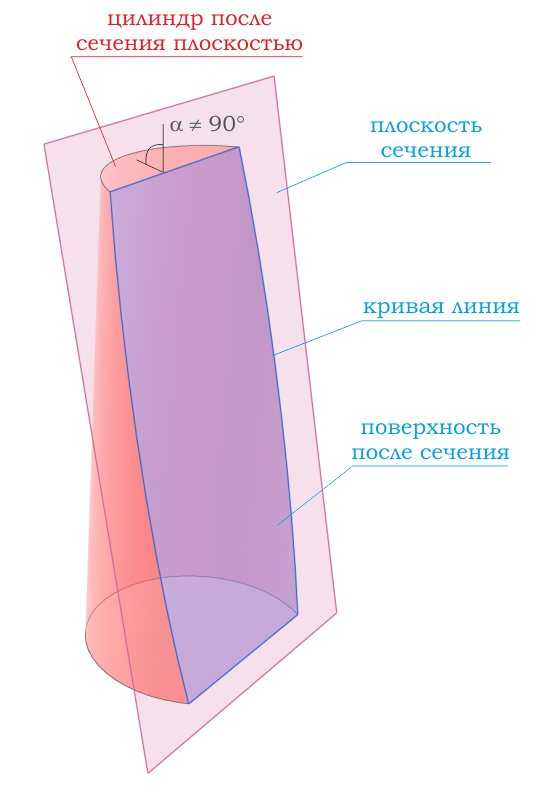
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет .

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается .

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде .

Определение объёма фигуры

Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.

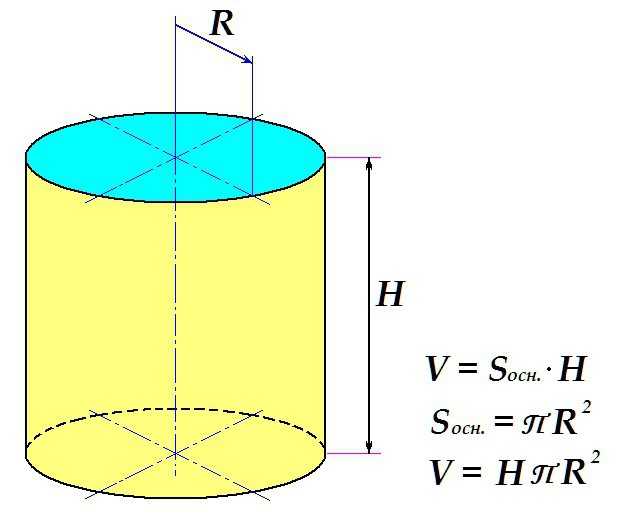
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П
и на квадрат радиуса основания.

Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.

Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N
. Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.

Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.

Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.

Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями — перпендикулярный отрезок, построенный между ними.

Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.

Определение и геометрические параметры

Высота цилиндра (h) определяет расстояние между его верхним и нижним основаниями. Радиус основания (r) является расстоянием от центра основания до любой точки этого основания.

Диаметр цилиндра (d) также является важной характеристикой. Диаметр определяется как удвоенное значение радиуса основания: d = 2r

Диагональ цилиндра (D) — это расстояние между двумя точками, лежащими на противоположных основаниях и проходящими через центр тела. Диагональ можно рассчитать с помощью теоремы Пифагора: D = √(h² + 4r²).

Знание геометрических параметров цилиндра позволяет более точно описать его форму и характеристики, а также использовать правильные формулы для расчетов.

Основные определения и принципы

Сечение цилиндра — это плоская фигура, получаемая при пересечении цилиндра и плоскости.

В сечении цилиндра выделяют следующие основные элементы:

1. Ось цилиндра — прямая линия, проходящая через центры основ цилиндра.
2. Плоскость сечения — плоская фигура, проходящая через цилиндр и образующая с ним пересечение.
3. Трансверсальная ось сечения — прямая линия, перпендикулярная оси цилиндра и проходящая через точку пересечения плоскости сечения с цилиндром.
4. Точка пересечения — точка, в которой плоскость сечения пересекает цилиндр.
5. Границы сечения — линии, образующие границы плоскости сечения.

При сечении цилиндра получаются различные фигуры в зависимости от угла наклона плоскости сечения и положения трансверсальной оси сечения. Вот некоторые примеры:

• Эллипс — когда плоскость сечения пересекает оба основания цилиндра под углом, равным тупому углу. Трансверсальная ось сечения проходит через центры обоих основ.
• Пара пересекающихся прямых — когда плоскость сечения пересекает только одно основание цилиндра и не пересекает его другое основание. Трансверсальная ось сечения пересекается с центральной осью цилиндра.
• Прямая линия — когда плоскость сечения проходит только через ось цилиндра и не пересекает его ни одно основание.

Изучение сечений цилиндра позволяет более глубоко понять его геометрию и свойства, а также применять их в решении различных математических задач.

Объем цилиндра. Площадь боковой поверхности цилиндра.Площадь полной поверхности цилиндра

      Для цилиндра с   r   и   h   (рис. 5)

Рис.5

введем следующие обозначения

V	объем цилиндра
Sбок	площадь
Sполн	площадь
Sосн	площадь

      Тогда справедливы следующие формулы для вычисления объема, площади :

S_осн = πr2,

V = S_оснh = πr2h,

S_бок= 2πrh,

S_полн = 2πr2 + 2πrh == 2π(r + h).

      Замечание 7. Формула объема цилиндра   V = πr2h   может быть получена из

при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Виды цилиндров

1. Прямой цилиндр – имеет одинаковые симметричные основания (круг или эллипс), параллельные друг другу. Отрезок между точками симметрии оснований перпендикулярен им, является осью симметрии и высотой фигуры.
2. Наклонный цилиндр – имеет одинаковые симметричные и параллельные друг другу основания. Но отрезок между точками симметрии не перпендикулярен этим основаниям.
3. Косой (скошенный) цилиндр – основания фигуры не взаимно параллельны.
4. Круговой цилиндр – основаниями является круг. Также выделяют эллиптические, параболические и гиперболические цилиндры.
5. Равносторонний цилиндр – прямой круговой цилиндр, диаметр основания которого равен его высоте.

Сами прямые называют образующими цилиндрической поверхности.
Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.

Так как все образующие и ось перпендикулярны плоскости альфа, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).

Если построить ещё одну плоскость бета, которая будет параллельна плоскости альфа, то отрезки образующих, заключённые между плоскостями альфа и бета будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости бета, дают окружность, равную окружности, лежащей в плоскости альфа.

Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях альфа и бета) называется цилиндром.
Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.

Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.

Сечения цилиндра различными плоскостями

Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого – образующие, а две другие – отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).

Основные формулы

Формула для вычисления площади боковой поверхности цилиндра: Sбок=2пRL.

То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: Sполн=2пR(R+L).

Примеры и разбор решения заданий тренировочного модуля

Дан цилиндр.

Выберите значение площади его боковой поверхности

1. 60π
2. 192π
3. 120π
4. 36π

Решение:

Площадь боковой поверхности вычисляется по формуле: S=2πRL.

R=6, L=10

Подставим: S=2π·6·10=120π.

Ответ: 3) 120π

Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.

Решение:

Sполн=2πR(R+L)

По условию задачи L=R+6.

144π=2πR(R+R+6).

Получили квадратное уравнение относительно радиуса:

R2+6R-72=0

R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.

Ответ: 12.

Задача

Осевое сечение цилиндра – квадрат со стороной 20 см. Найти высоту цилиндра, радиус цилиндра, ось цилиндра и площадь основания цилиндра.

Решение

Одна из сторон осевого сечения – образующая (она же равна оси цилиндра и она же равна высоте). Значит, высота и ось равны 20 см. Далее, вторая сторона осевого сечения – диаметр основания. Он равен 20 см, значит, радиус – 10 см. Наконец, площадь основания ищется по формуле

Итак, ребята, на этом уроке мы изучили, что такое цилиндрическая поверхность, её образующая; цилиндр, все его элементы и сечения; площади поверхностей цилиндра.

Примеры задач

Задание №1.
Дан прямой цилиндр, площадь основания которого 12,56 см 2 . Необходимо вычислить полную площадь цилиндра, если его высота равна 3 см.

Решение. Необходимо воспользоваться формулой для полной площади кругового прямого цилиндра. Но в ней не хватает данных, а именно радиуса основания. Зато известна площадь круга. Из нее легко вычислить радиус.

Он оказывается равным квадратному корню из частного, которое получается от деления площади основания на пи. После деления 12,56 на 3,14 выходит 4. Квадратный корень из 4 — это 2. Поэтому радиус будет иметь именно такое значение.

Ответ: S пол = 50,24 см 2 .

Задание №2.
Цилиндр с радиусом 5 см пресечен плоскостью, параллельной оси. Расстояние от сечения до оси равно 3 см. Высота цилиндра — 4 см. Требуется найти площадь сечения.

Решение. Форма сечения — прямоугольная. Одна его сторона совпадает с высотой цилиндра, а другая равна хорде. Если первая величина известна, то вторую нужно найти.

Для этого следует сделать дополнительное построение. В основании проводим два отрезка. Оба они будут начинаться в центре окружности. Первая будет заканчиваться в центре хорды и равняться известному расстоянию до оси. Вторая — на конце хорды.

Получится прямоугольный треугольник. В нем известны гипотенуза и один из катетов. Гипотенуза совпадает с радиусом. Второй катет равен половине хорды. Неизвестный катет, умноженный на 2, даст искомую длину хорды. Вычислим его значение.

Для того чтобы найти неизвестный катет, потребуется возвести в квадрат гипотенузу и известный катет, вычесть из первого второе и извлечь квадратный корень. Квадраты равны 25 и 9. Их разность — 16. После извлечения квадратного корня остается 4. Это искомый катет.

Хорда будет равна 4 * 2 = 8 (см). Теперь можно вычислить площадь сечения: 8 * 4 = 32 (см 2).

Ответ: S сеч равна 32 см 2 .

Задание №3.
Необходимо вычислить площадь осевого сечения цилиндра. Известно, что в него вписан куб с ребром 10 см.

Решение. Осевое сечение цилиндра совпадает с прямоугольником, который проходит через четыре вершины куба и содержит диагонали его оснований. Сторона куба является образующей цилиндра, а диагональ основания совпадает с диаметром. Произведение этих двух величин даст площадь, которую нужно узнать в задаче.

Для поиска диаметра потребуется воспользоваться знанием того, что в основании куба — квадрат, а его диагональ образует равносторонний прямоугольный треугольник. Гипотенуза его является искомой диагональю фигуры.

Для ее расчета потребуется формула теоремы Пифагора. Нужно возвести в квадрат сторону куба, умножить ее на 2 и извлечь квадратный корень. Десять во второй степени — это сто. Умноженное на 2 — двести. Квадратный корень из 200 равен 10√2.

Сечение — это снова прямоугольник со сторонами 10 и 10√2. Его площадь легко сосчитать, перемножив эти значения.

Ответ. S сеч = 100√2 см 2 .

Представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.

Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:

Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы. Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру. Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.

Понятие конуса

Построим на плос-ти α окруж-ть L с центром в точке О. Далее через О проведем перпендикуляр к α и отметим на нем точку Р. Если мы отрезками соединим точку Р с каждой точкой окруж-ти L, то получим поверх-ть, которая именуется конической поверхностью. При этом:

• прямая ОР – это ось конической поверх-ти;
• прямые, соединяющие Р с точками на окруж-ти L, именуются образующими конической поверх-ти;
• сама точка Р – это вершина конической поверх-ти.

Объемное тело, ограниченное окруж-тью L и конической поверх-тью, именуется конусом. Соответственно вершина конической поверх-ти, её ось и образующие будут одновременно являться вершиной, осью и образующими конуса. Окруж-ть L – это основание конуса.

Ещё несколько терминов:

• коническая поверх-ть конуса именуется его боковой поверх-тью;
• если же к этой площади прибавить ещё и площадь основания, то в итоге получится полная площадь конуса;
• отрезок ОР – это не только ось конуса, но и высота конуса.

Как и в случае с цилиндром, мы в данном случае рассматриваем особый случай конуса – прямой круговой конус. В более общем случае ось конуса может не быть перпендикуляром к плос-ти основания (так называемый косой конус). Также в его основании может находиться не окруж-ть, а другая плоская фигура.

В общем случае любая пирамида может рассматриваться как частный случай конуса. Однако в рамках школьного курса под конусом подразумевается исключительно прямой круговой конус, если только не обговорено иное.

Докажем важное утверждение:

Действительно, рассмотрим две произвольные образующие РА и РВ у конуса с вершиной Р, у которой О – центр основания:

Так как ось ОР перпендикулярна основанию, то ∆РОА и ∆РОВ – прямоугольные. У них общий катет РО, а катеты АО и ОВ одинаковы как радиусы окруж-ти. Тогда ∆РОА и ∆РОВ равны, поэтому одинаковы и образующие РА и РВ, ч. т. д.

Заметим, что конус получается при вращении прямоугольного треуг-ка вокруг его катета. Так, на следующем рисунке конус получается при вращении ∆РОА с прямым углом О относительно катета РО:

Если сечение конуса проходит через его ось, то оно именуется осевым сечением. Ясно, что это сечение будет являться треуг-ком, причем две его стороны – это образующие конуса, а третья сторона диаметр основания. Образующие конуса одинаковы, поэтому осевое сечение будет равнобедренным треуг-ком.

Теперь рассмотрим сечение, параллельное плос-ти основания. Пусть оно пересекает ось РО в какой-то точке О₁. Также пусть А₁ – точка пересечения образующей АР исходного конуса с секущей плос-тью α:

Заметим, что раз ось РО перпендикулярна основанию, то она также будет перпендикулярна и секущей плос-ти, ведь основание и плос-ть α параллельны. Тогда ∠РО₁А₁ будет прямым.

Теперь рассмотрим ∠РОА и ∠РО₁А₁. Они прямоугольные и у них есть общие угол ∠АРО. Значит, это подобные треуг-ки. Обозначим радиус ОА как r, а длину А₁О₁ как r₁. Тогда из подобия получаем:

Рассмотрим теперь другую образующую ВР, которая пересекает секущую плос-ть в точке В₁. Отрезки АО и ОВ одинаковы. Повторяя предыдущие рассуждения, легко доказать подобие ∆РОВ и ∆РО₁В₁, откуда можно вычислить длину О₁В₁:

Получили, что точки А₁и В₁ находятся на одинаковом расстоянии r₁ от точки О₁. Мы выбрали точки А и В произвольно, поэтому для любых двух точек, принадлежащих сечению конуса, можно утверждать, что они равноудалены от точки О₁. Это значит, что все точки сечения лежат на окруж-ти с центром в точке О₁ и радиусом r₁, то есть сечение имеет форму окруж-ти.

Как определить площадь боковой поверхности конуса? Для этого ее надо «разрезать» вдоль одной из образующих и развернуть на плос-ти. В результате получится круговой сектор.

Напомним, что площадь сектора может быть рассчитана по формуле

Теперь обозначим длину образующей буквой l, а радиус основания конуса как r. Тогда

Для вычисления полной площади конуса к боковой поверх-ти необходимо добавить ещё и площадь основания:

Заключение

На этом уроке мы узна­ли о ци­лин­дри­че­ской по­верх­но­сти, видах ци­лин­дра, эле­мен­тах ци­лин­дра и сход­стве ци­лин­дра с приз­мой.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/11-klass/btela-vraweniya-b/ponyatie-tsilindra

https://www.youtube.com/watch?v=eLv-lSek-60

https://www.youtube.com/watch?v=P7_5qWj2BZM

http://dok.opredelim.com/docs/index-7319.html

http://mypresentation.ru/download/125438_ponyatie_cilindra__prezentaciya_po_geometrii

http://fs1.ppt4web.ru/uploads/ppt/95242/50208d20656afdeb627a755fe2f9813e.ppt

http://mateshka.ru/matematika/tela-vrasheniya.html

http://math4school.ru/tela_vrashhenija.html#spr1301

http://www.stendzakaz.ru/images/school/k-geom/k-geom-30.jpg