Вписанные и описанные тела. цилиндр, описанный около призмы цилиндр можно описать около прямой призмы если ее основание

Способы измерения размеров цилиндра

Для определения объема цилиндра, важно точно знать его размеры. Вот несколько способов измерить главные параметры цилиндра:. Диаметр — это расстояние между двумя точками, проходящими через центры противоположных сторон цилиндра

Для измерения диаметра можно использовать линейку, штангенциркуль или другой подходящий инструмент

Диаметр — это расстояние между двумя точками, проходящими через центры противоположных сторон цилиндра. Для измерения диаметра можно использовать линейку, штангенциркуль или другой подходящий инструмент.

Высота — это расстояние от одной плоскости основания цилиндра до другой параллельной плоскости. Её также можно измерить с помощью линейки или другого измерительного инструмента.

Объем цилиндра можно вычислить, используя формулу V = π * r^2 * h, где r — радиус основания, а h — высота. Радиус можно найти, разделив диаметр на 2.

Следуя этим простым способам, вы сможете точно измерить размеры цилиндра и рассчитать его объем.

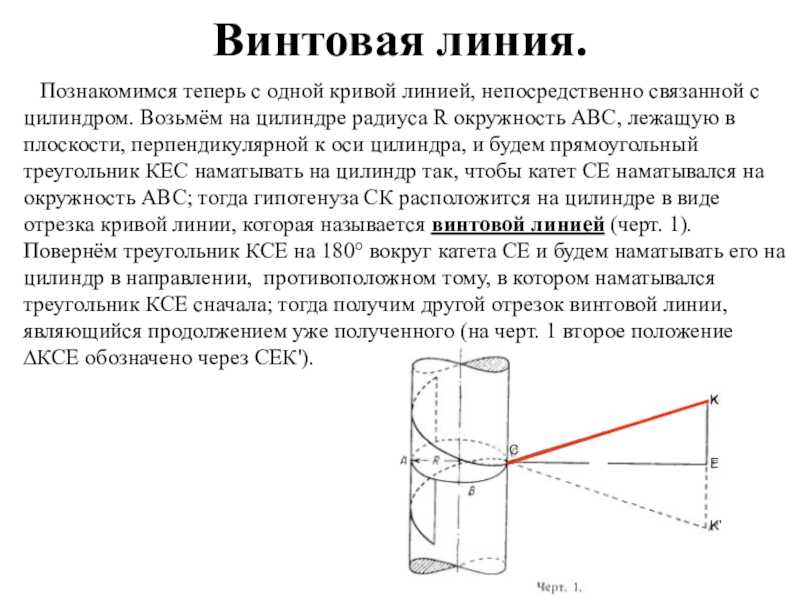
Слайд 39Винтовая линия.Познакомимся теперь с одной кривой линией, непосредственно связанной с цилиндром.

Возьмём на цилиндре радиуса R окружность ABC, лежащую в плоскости, перпендикулярной к оси цилиндра, и будем прямоугольный треугольник КЕС наматывать на цилиндр так, чтобы катет СЕ наматывался на окружность ABC; тогда гипотенуза СК расположится на цилиндре в виде отрезка кривой линии, которая называется винтовой линией (черт. 1). Повернём треугольник КСЕ на 180° вокруг катета СЕ и будем наматывать его на цилиндр в направлении, противоположном тому, в котором наматывался треугольник КСЕ сначала; тогда получим другой отрезок винтовой линии, являющийся продолжением уже полученного (на черт. 1 второе положение ∆КСЕ обозначено через СЕК’).

C

K

E

K’

Определение и применение в геометрии

Объем цилиндра можно найти с использованием формулы: V = π * r^2 * h, где V – объем, π – число «пи» (приблизительно равное 3,14159), r – радиус основания цилиндра, h – высота цилиндра. Данная формула позволяет точно определить объем цилиндра и использовать его в различных применениях.

Объем цилиндра широко применяется в геометрии, строительстве, механике и других областях науки и техники. В геометрии объем цилиндра позволяет находить объем тел и фигур, связанных с этой геометрической формой. В строительстве, например, объем цилиндра используется при расчете площади поверхности цилиндрических емкостей или трубопроводов.

Помимо этого, объем цилиндра находит применение в механике при расчете объема жидкостей, находящихся в цилиндрических емкостях или цилиндрических штоках и поршнях. Знание объема цилиндра позволяет определить массу, плотность и другие характеристики вещества, находящегося внутри цилиндрической формы.

Слайд 42Винтовые линии бывают правовинтовые и левовинтовые.Предположим, что по винтовой линии движется

точка. Проекцией винтовой линии на плоскость, перпендикулярную кеё оси (будем называть осью винтовой линии ось цилиндра, на котором она расположена), будет, очевидно, окружность. Поэтому если смотреть на винтовую линию в направлении её оси, то будет казаться, что точка движется по окружности. Если точка движется по окружности по часовой стрелке, удаляясь от нас, то винтовая линия называется право- винтовой, если же она движется по часовой стрелке, приближаясь к нам, то винтовая линия называется левовин- товой. Правовинтовую и левовинтовую линии на одном итом же цилиндре с одинаковым углом подъёма совместить нельзя. На черт.1 у нас получилась левовинтовая линия; чтобы получить правовинтовую линию, нужно наматывать треугольник в противоположном направлении.

Слайд 53С примерами винтовой линии мы часто встречаемся в физике и технике.

Форму винтовой линии с очень малым углом имеет каждый слой проволоки в индукционной катушке. При равномерной подаче резец токарного станка при обточке цилиндра оставляет на этом цилиндре след в виде винтовой линии. Форму винтовой линии имеет режущая кромка цилиндрических спиральных свёрл. Форма нарезки на всякого рода скрепляющих, регулировочных винтах, болтах и гайках — винтовая линия (причём, как правило, применяется правовинтовая нарезка). При прямолинейном равномерном полёте точка на пропеллере самолёта описывает винтовую линию. Точно так же винтовую линию описывает точка на гребном винте как океанского парохода, так и моторной лодки. Форму винтовой линии имеет штопор, употребляемый для раскупоривания бутылок. Винтовую линию описывает точка крыла самолёта, когда он «входит в штопор». При прямолинейном равномерном полёте винтовочной пули, а также артиллерийского снаряда точки на их поверхности описывают винтовые линии. Во всех перечисленных примерах научно-технического характера при производимых расчётах используются те или иные свойства винтовой линии. Число и характер приведённых примеров говорят о важных практических применениях винтовой линии.

Слайд 52Винтовые линии в нашей жизни. В природе форму винтовой

линии имеют усики вьющихся растений. Для примера можно указать на усики винограда, хмеля, фасоли, гороха и других растений, причём усики, закручиваясь, образуют правовинтовую линию, если усик встречает опору слева от себя. Если же при своём перемещении (так называемое, нутационное движение усика, при котором усик описывает в пространстве конус) вертикальная опора встречается справа, то, обвиваясь вокруг этой опоры, усик образует левовинтовую линию. Что касается стеблей вьющихся растений, то они обвиваются вокруг опоры также по винтовой линии, но при этом каждый вид завивается в совершенно определённом направлении. Большинство вьющихся растений, обвиваясь, образует правовинтовую линию; в качестве примера можно привести фасоль, крученый паныч, вьюнок полевой, батат и др.; лево- винтовую линию образуют хмель и жимолость.

Как описать цилиндр вокруг призмы

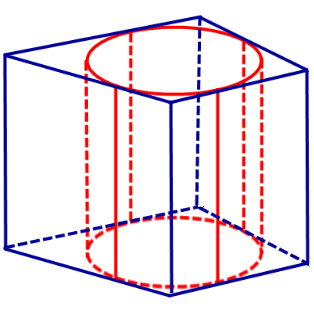
Говорят, что цилиндр вписан в призму (или призма описана около цилиндра), если основания цилиндра вписаны в соответствующие основания призмы (рис. 1). Очевидно, что их высоты совпадут (рис. 2).

Рис. 1. Цилиндр, вписанный в призму

Рис. 2. Цилиндр, вписанный в призму

Нужно, чтобы в основание призмы можно было вписать окружность. Что для треугольной и правильной призмы верно всегда (рис. 3, 4).

Рис. 3. Цилиндр, вписанный в треугольную призму

Рис. 4. Цилиндр, вписанный в правильную шестиугольную призму

Вывод: цилиндр можно вписать в призму, если призма прямая, а в ее основание можно вписать окружность.

Для четырехугольный призмы необходимо чтобы призма была также прямой, а четырехугольник в основании был описанным. Т. е. суммы противоположных сторон были равны (рис. 5).

Рис. 5. Цилиндр, вписанный в четырехугольную призму

Условие: в правильную треугольную призму, все ребра которой равны 6, вписан цилиндр. Найти его радиус и высоту (рис. 6).

Рис. 6. Иллюстрация к задаче 1

Заметим, что высота цилиндра равна высоте призмы, а значит, равна 6.

Радиус основания цилиндра равен радиусу окружности, вписанной в правильный треугольник со стороной 6. Радиус этой окружности находим по формуле

Ответ: .

Говорят, что цилиндр можно описать около призмы (или призму вписать в цилиндр), если основания призмы вписаны в основания цилиндра. В данном случае, очевидно, снова будут равны высоты (боковые стороны призмы и образующие цилиндра) (рис. 7).

Рис. 7. Цилиндр, описанный около призмы

Цилиндр можно описать около призмы, когда основание призмы можно вписать в окружность. Для треугольной -угольной правильной призмы – всегда, для четырехугольной – когда сумма противоположных углов в основании дает 180 градусов (рис. 8).

Рис. 8. Цилиндр, описанный около четырехугольной призмы

Условие: дана правильная шестиугольная призма, вписанная в цилиндр. Радиус основания цилиндра равен 7, а площадь боковой поверхности цилиндра равна 28. Найти площадь боковой поверхности призмы (рис. 9).

Рис. 9. Иллюстрация к задаче 2

Сперва найдем высоту цилиндра. Так как

Значит, и боковое ребро призмы также равно 2.

Далее, в основании призмы лежит правильный шестиугольник, вписанный в окружность. Как известно, сторона правильного шестиугольника равна радиусу описанной окружности, то есть 7.

Тогда площадь боковой поверхности призмы равна .

Условие. Дана четырехугольная прямая призма, все ребра которой равны 1. Известно, что около этой призмы можно описать цилиндр. Найдите объем призмы и площадь полной поверхности данного цилиндра (рис. 10).

Рис. 10. Иллюстрация к задаче 3

Так как все ребра равны, то в основании призмы лежит ромб. Раз можно описать цилиндр около призмы, то ромб можно вписать в окружность, а значит, этот ромб – квадрат. Следовательно, призма – это куб со стороной 1, его объем также равен 1.

Высота цилиндра – 1, а радиус окружности равен половине диагонали квадрата, то есть

Ответ: .

На уроке мы разобрали комбинации призмы и цилиндра, а также решили задачи по темам: цилиндр, описанный вокруг призмы и цилиндр, вписанный в призму.

Список литературы

1. Атанасян Л.С. и др. Геометрия. Учебник для 10-11 классов.
2. Погорелов А.В. Геометрия. Учебник для 10-11 классов.
3. Бевз В.Г., Владимирова Н.Г. Геометрия 11 класс.

Домашнее задание

1. В правильную треугольную призму, все ребра которой равны 12, вписан цилиндр. Найти его радиус и высоту.
2. Дана правильная шестиугольная призма, вписанная в цилиндр. Радиус основания цилиндра равен 10, а площадь боковой поверхности цилиндра равна 100. Найти площадь боковой поверхности призмы.
3. Дана четырехугольная прямая призма, все ребра которой равны 2. Известно, что около этой призмы можно описать цилиндр. Найдите объем призмы и площадь полной поверхности данного цилиндра.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Определение переменных

Прежде чем приступить к вычислению объема цилиндра вокруг призмы, нам нужно определить несколько переменных:

Радиус основания призмы (r) — это расстояние от середины основания до любой точки его окружности. Радиус обычно измеряется в единицах длины, таких как сантиметры или метры.

Высота призмы (h) — это вертикальная длина призмы, измеренная от одного основания до другого. Высота обычно измеряется в тех же единицах длины, что и радиус.

Высота цилиндра (H) — это вертикальная длина цилиндра, которая также измеряется в тех же единицах длины.

Радиус цилиндра (R) — это расстояние от центра цилиндра (центра основания призмы) до его окружности.

При определении этих переменных и использовании соответствующих значений в формуле, мы сможем вычислить объем цилиндра вокруг призмы.

Слайд 49В него входят: помощь при сердечно-сосудистых заболеваниях, нейротрофических заболеваниях, гипертонии, болезнях

выводящих путей, астме, бессоннице, головных болях, а также в качестве средства для снятия стрессов и профилактике атеросклероза. Одна из удивительных особенностей Цилиндров Фараона — улучшение работы практически всех основных систем организма (показатели работы этих систем улучшаются в среднем в 2 — 2.5 раза).Согласно мнению ряда врачей, Цилиндры Фараона представляют собой уникальный, самонастраивающийся на каждого человека, физиотерапевтический прибор, созданный гением древнеегипетских ученых. Их целебные свойства, включающие в себя металлотерапию, гальванотерапию и магнитотерапию позволили врачу-биоэнергетику Т.Мешковой разработать эффективную методику использования Цилиндров. Цилиндры Фараона полезны как взрослым людям, так и детям. Они создают в организме человека обстановку, при которой ему гораздо легче справляться со своими бедами. Цилиндры — прекраснее профилактическое средство против ряда болезней. Согласно результатам экспериментов врача Т.Мешковой, Цилиндры Фараона защищают от воздействия излучений различной электронной техники: компьютеров, телевизоров, микроволновых печей и т.д.

Слайд 5Вклад Евклида в математику.О Евклиде почти ничего неизвестно, откуда он был

родом, где и у кого учился.Папп Александрийский (III в.) сообщает, что он был очень доброжелателен ко всем тем, кто сделал хоть какой-нибудь вклад в математику, корректен, в высшей степени порядочен и совершенно лишен тщеславия. Евклид, как и другие великие греческие геометры, занимался астрономией, оптикой и теорией музыки. До нас дошли его сочинения, посвященные прикладным вопросам: «Феномены» (элементарная сферическая астрономия), «Оптика» (учение о перспективе) и «Сечение канона» ( теория музыки). Это были первые прообразы будущих исследований по математической физике: в них теория выводилась строго дедуктивно из явно сформулированных физических гипотез и математических постулатов. Гораздо больше мы знаем о математическом творчестве Евклида. Прежде всего Евклид является для нас автором «Начал», по которым учились математики всего мира. Эта удивительная книга пережила более двух тысячелетии, но до сих пор не утратила своего значения не только в истории науки, но и самой математике. Созданная там система евклидовой геометрии и теперь изучается во всех школах мира и лежит в основе почти всей практической деятельности людей. На геометрии Евклида базируется классическая механика, ее апофеозом было появление в 1687 г. Математических начал натуральной философии Ньютона, где законы земной и небесной механики и физики устанавливаются в абсолютном евклидовом пространстве. Содержание «Начал» далеко не исчерпывается элементарной геометрией — это основы всей античной математики. Здесь подводится итог более чем 300-летнему ее развитию и вместе с тем создается прочная 6aзa для дальнейших исследований. Последующие математики ссылались на предложения «Начал», как на нечто окончательно установленное.

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра

      Определение 1. Цилиндром, вписанным в призму, называют такой , окружности которого вписаны в , являющиеся , а (рис. 1).

Рис.1

      Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.

      Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.

       Утверждение 1. Если в можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен

      Доказательство. Рассмотрим призму   A₁A₂ … A_nA’₁A’₂ … A’_n,   у которой в   A₁A₂ … A_n   и   A’₁A’₂ … A’_n   можно вписать окружности. Пусть в нижнее   A₁A₂ … A_n   призмы   A₁A₂ … A_nA’₁A’₂ … A’_n   вписана окружность с центром   O   радиуса   r,   которая касается прямой   A₁A₂   в точке   K .   Проведем через точку   O   прямую, параллельную   A₁A’₁   призмы и пересекающую плоскость верхнего в точке   O’   (рис. 2).

Рис.2

      Вследствие плоскость   KOO’  параллелельна боковому ребру   A₁A’₁ ,   а ее линия пересечения   KK’   с боковой гранью призмы   A₁A₂A’₁A’₂     Замечая, что отрезки   OK   и   O’K’  , заключаем, что четырехугольник   OO’K’K   – .

      Поскольку   OK  – это радиус окружности, проведенный в точку касания окружности радиуса   r   с центром   O   и прямой A₁A₂ ,   то   . Значит, и   O’K’ = r   и угол   O’K’A’₁   равен 90°, то есть

     Рассуждая аналогичным образом, заключаем, что точка   O’  равноудалена от всех прямых, на которых лежат ребра верхнего основания   A’₁A’₂,   A’₂A’₃,   … ,   A_{n – 1}A_n,   а поскольку  O’   лежит в плоскости верхнего основания, то точка   O’   является центром вписанной в многоугольник   A’₁A’₂ … A’_n   окружности.

      В силу того, что прямые   OO’   и   A₁A’₁   параллельны по построению, а прямые OA₁   и   O’A’   параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник   OO’A₁A’₁   является , откуда вытекает равенство:   OO’ = A₁A’₁.

      Утверждение 1 доказано.

      Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:

1. Призма является ;
2. В основания призмы можно вписать окружности.

      Доказательство. Докажем сначала, что если в   n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.

      Действительно, выполнение условия 2 следует непосредственно из Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.

      С этой целью рассмотрим ось цилиндра   OO’ ,   соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).

Рис.3

      Согласно отрезок   OO’   параллелен боковым ребрам призмы. Поскольку ось цилиндра   OO’   перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.

      Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.

      Теперь рассмотрим   h,   в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.

      Обозначим буквой   O   центр окружности радиуса   r,   вписанной в нижнее основание призмы, а символом   O’   обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).

Рис.4

      Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно отрезок   OO’   параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы   h.   Значит, и отрезок   OO’   перпендикулярен плоскости основания призмы и равен   h.

     Цилиндр с осью   OO’,   радиусом   r   и высотой   h   и будет вписан в исходную призму.

      Доказательство теоремы завершено.

      Следствие 1 . , описанной около цилиндра, равна

      Следствие 2. В любую можно вписать цилиндр.

      Справедливость этого утверждения вытекает из того факта, что

      Следствие 3. В любую можно вписать цилиндр.

      Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.

Элементы треугольной призмы

Треугольники ABC и A₁B₁C₁ являются основаниями призмы .

Четырехугольники A₁B₁BA, B₁BCC₁ и A₁C₁CA являются боковыми гранями призмы .

Стороны граней являются ребрами призмы (A₁B₁, A₁C₁, C₁B₁, AA₁, CC₁, BB₁, AB, BC, AC), всего у треугольной призмы 9 граней.

Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

Способы нахождения объема цилиндра

1. Формула с использованием радиуса и высоты

Наиболее распространенным способом нахождения объема цилиндра является использование его радиуса (R) и высоты (h). Формула для расчета объема цилиндра в этом случае будет следующей:

V = П * R^2 * h

2. Формула с использованием диаметра и высоты

Если известен диаметр (D) цилиндра, то объем можно найти, используя следующую формулу:

V = (П/4) * D^2 * h

3. Формула с использованием площади основания и высоты

Если известна площадь (S) основания цилиндра, то объем можно найти, используя следующую формулу:

V = S * h

4. Использование воды и мерной емкости

Практический способ нахождения объема цилиндра заключается в его заполнении водой и измерении объема воды с помощью мерной емкости. Для более точного результата рекомендуется использовать воду без пузырей и уравновешенно устанавливать цилиндр на горизонтальной поверхности.

Не важно, каким способом вы будете пользоваться, все они дают точные результаты, если правильно измерить данные и соблюсти технику безопасности

Как найти площадь основания призмы?

Основание призмы может быть различной формы: квадрат, прямоугольник, треугольник, круг и т.д. В каждом случае для нахождения площади основания применяются соответствующие формулы.

Например, для квадратной призмы площадь основания равна квадрату длины стороны: S = a^2, где a — длина стороны основания.

Для прямоугольной призмы площадь основания равна произведению длины и ширины: S = l * w, где l — длина, w — ширина.

Если основание призмы имеет форму треугольника, площадь можно найти с помощью формулы Герона: S = sqrt(p * (p — a) * (p — b) * (p — c)), где a, b и c — длины сторон треугольника, p — полупериметр (сумма всех сторон, деленная на 2).

Для нахождения площади основания, имеющего форму круга, используется формула площади круга: S = pi * r^2, где pi — число Пи (приближенное значение равно 3,14), r — радиус круга.

В общем случае, для нахождения площади основания призмы необходимо знать форму основания и использовать соответствующую формулу. Это позволит точно определить площадь основания и продолжить расчеты для нахождения объема призмы описанного около цилиндра.

Многоугольник. Цилиндр описанный вокруг призмы.

Цилиндр считается описанным вокруг призмы, когда он соответствует требованию — основание, многоугольник, вписан в окружность.

Перефразировав формулировку имеем, призма вписана в цилиндр, когда ее основания вписаны в основания цилиндра, а боковые ребра выступают образующими призмы.

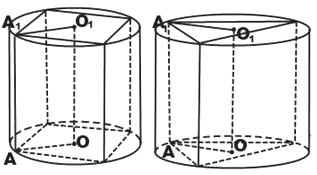
Как видим, высоты вписанной призмы и цилиндра одинаковы.

В программе среднего образования представлен лишь прямой круговой цилиндр, следовательно, вписанная в цилиндр призма будет прямой.

Призму реально вписать в цилиндр, когда существует возможность вокруг ее основания описать окружность. Значит, в цилиндр получиться вписать правильную призму, прямую треугольную призму, прямоугольный параллелепипед.

Ось цилиндра расположена на одной прямой линии с высотой призмы, объединяющей центры окружностей описанных вокруг призмы.

При выполнении заданий на призму, вписанную в цилиндр, допускается провести анализ отдельного элемента сечения комбинации фигур — прямоугольника, ребра у него равняются радиусу описанной вокруг основания призмы окружности (радиусу цилиндра) и высоте призмы (и цилиндра).

Так, к примеру, рассмотрим АА₁О₁О — прямоугольник, высота призмы и цилиндра представлена ОО₁=Н, а R радиус описанной окружности равняется AO.

Через площадь грани и ребро основания

Ребро основания равняется длине любого отрезка в равностороннем треугольнике внутри призмы. Граней у
призмы 3. Две боковые и одна задняя. Они изображены в виде параллелограммов. Зная длину и площадь
грани у призмы, можно воспользоваться следующую формулу для расчета высоты правильной треугольной
призмы:

H = S / a

где S — площадь грани, a — ребро основания.

Цифр после
запятой:

Результат в:

Пример. Если S = 5 мм², а = 8 мм² то вычисления H будут производиться следующим
способом: H = 5 / 8 = 0,62 мм. С помощью этой формулы можно найти искомую
величину.

Умение рассчитать высоту треугольного многогранника пригодится при решении геометрических задач.
Знания могут потребоваться в школе, в университете, но иногда такая необходимость может возникнуть в
реальной жизни. Например, как строитель сможет посчитать площадь дома в виде призмы, если не знает
расчетной формулы

Важно понимать, как найти неизвестные переменные, когда известно лишь несколько
параметров

Задачи на расчет треугольной призмы

Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы. Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:

V = 1/2 · 6 · 8 · 5 = 120.

Задача 2.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Решение:

Объём призмы равен произведению площади основания на высоту: V = S_осн ·h.

Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S₂ = S₁k 2 = S₁2 2 = 4S₁.

Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.

Слайд 6Вклад Кавальери в математику.

В своем основном труде «Геометрия» (1635г.) Кавальери развил разработанный им задолго до выхода книги новый метод определения площадей и объемов – так называемый метод неделимых. Неделимыми Кавальери называл параллельные между собой хорды плоской фигуры или параллельные плоскости тела. Важнейший признак неделимости состоит в том, что число измерений его на единицу меньше самого геометрического образа. У плоской фигуры 2 измерения, у ее неделимого, т.е. у отрезка – 1 измерение. Кавальери доказал теорему о том, что площади двух подобных фигур относятся как квадраты, а объемы – как кубы соответствующих неделимых, и установил, что отношение суммы квадратов всех неделимых треугольника к сумме квадратов всех неделимых параллелограмма, имеющего с треугольником одинаковые основания и высоту, равно 1:3. Впоследствии Кавальери нашел аналогичные соотношения для суммы кубов и т.д. до девятой степени неделимых. Труды Кавальери сыграли огромную роль в формировании исчисления бесконечно малых.

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра

Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.

Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.

Утверждение 1. Если в основания призмы можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен боковому ребру призмы.

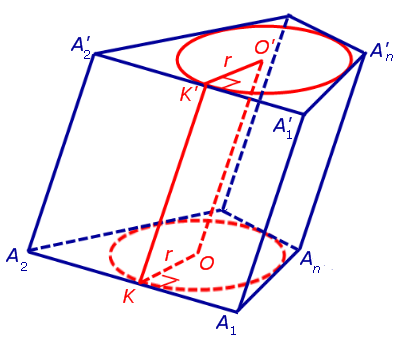
Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’₁A’₂, A’₂A’₃, . , A_{n – 1}A_n , а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’₁A’₂ . A’_n окружности.

В силу того, что прямые OO’ и A₁A’₁ параллельны по построению, а прямые OA₁ и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A₁A’₁ является параллелограммом, откуда вытекает равенство: OO’ = A₁A’₁ .

Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:

1. Призма является прямой призмой;
2. В основания призмы можно вписать окружности.

Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, вписанного в призму. Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.

С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).

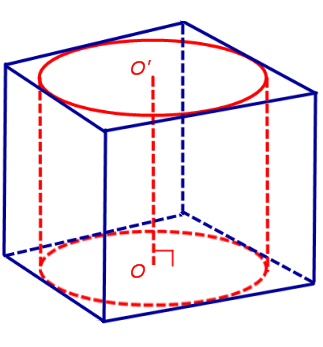
Согласно утверждению 1 отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.

Теперь рассмотрим прямую n – угольную призму высоты h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.

Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).

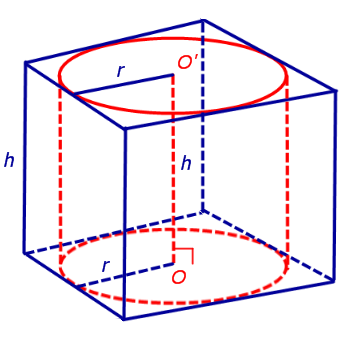
Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Цилиндр с осью OO’ , радиусом r и высотой h и будет вписан в исходную призму.

Доказательство теоремы завершено.

Следствие 1 . Высота призмы, описанной около цилиндра, равна высоте цилиндра.

Следствие 2. В любую прямую треугольную призму можно вписать цилиндр.

Справедливость этого утверждения вытекает из того факта, что в любой треугольник можно вписать окружность.

Следствие 3. В любую правильную n – угольную призму можно вписать цилиндр.

Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.