Егэ по математике объем цилиндра

Что такое файл cookie и другие похожие технологии

Файл cookie представляет собой небольшой текстовый файл, сохраняемый на вашем компьютере, смартфоне или другом устройстве, которое Вы используете для посещения интернет-сайтов.

Некоторые посещаемые Вами страницы могут также собирать информацию, используя пиксельные тэги и веб-маяки, представляющие собой электронные изображения, называемые одно-пиксельными (1×1) или пустыми GIF-изображениями.

Файлы cookie могут размещаться на вашем устройстве нами («собственные» файлы cookie) или другими операторами (файлы cookie «третьих лиц»).

Мы используем два вида файлов cookie на сайте: «cookie сессии» и «постоянные cookie». Cookie сессии — это временные файлы, которые остаются на устройстве пока вы не покинете сайт. Постоянные cookie остаются на устройстве в течение длительного времени или пока вы вручную не удалите их (как долго cookie останется на вашем устройстве будет зависеть от продолжительности или «времени жизни» конкретного файла и настройки вашего браузера).

Конус

В школе рассматривают не конус вообще, а только прямой круговой конус, называя его просто конусом. Поэтому вместо общего определения используем следующий факт:

Прямой круговой конус можно рассматривать как тело, полученное вращением прямоугольного треугольника вокруг его катета.

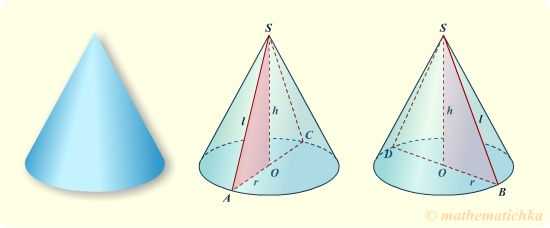
На рисунках изображен конус, полученный вращением закрашенного треугольника. Таким образом, ΔASO и ΔOSB — это, по существу, один и тот же треугольник в разных положениях при вращении вокруг оси SO. Катет SO является высотой конуса — h, второй катет (AO = OB) равен радиусу основания — r, длина гипотенузы (SA = SB) равна длине образующей — l. Такое определение конуса даёт нам сразу две подсказки, как перейти к планиметрии: — сечение плоскостью, проходящей через ось вращения, (обычно, это вертикальное сечение) позволяет свести задачу к рассмотрению прямоугольного или равнобедренного треугольника, — сечение плоскостью, перпендикулярной оси вращения, (обычно, это горизонтальное сечение) позволяет свести задачу к свойствам круга.

Ниже вы видите чертежи на плоскости вместе с формулами, которыми можно пользоваться в этом разделе. На синем рисунке представлены развёртка боковой поверхности конуса и его основание.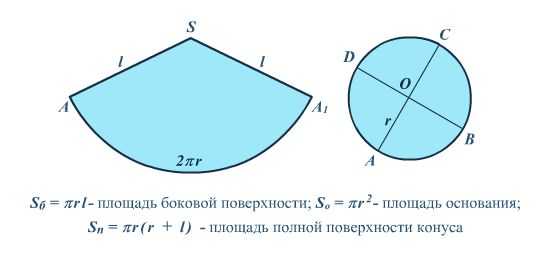

На красном рисунке — осевое сечение конуса со всеми обозначениями, которые могут понадобиться при решении следующих трёх задач.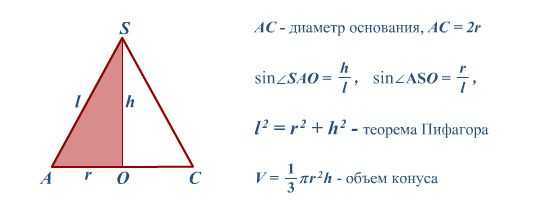

Внимание:1) В решениях задач часто встречаются рисунки, дождитесь их полной загрузки. 2) Для усиления обучающего эффекта ответы и решения загружаются отдельно для каждой задачи последовательным нажатием кнопок на желтом фоне

(Когда задач много, кнопки могут появиться с задержкой. Если кнопок не видно совсем, проверьте, разрешен ли в вашем браузере JavaScript.)

Задача 1

Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.

Решение

1) Чертим треугольник SAO (выше есть готовый чертеж). 2) Делаем краткую запись задачи, соотнося всё с чертежом. Дано: SO = h = 4, AC = 2r = 6. Найти: SA = l = ?
3) Подставляем значения с чертежа в известные формулы: l 2 = r 2 + h 2; r = 6/2 = 3; l 2 = 32 + 42 = 9 + 16 = 25; l 2 = 25; l = 5.

Ответ: 5

Задача 2.

Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.

Решение

Порядок наших действий такой же, как в предыдущей задаче: чертеж, краткая запись, формулы. Только в конце неизвестная величина оказывается в правой части равенства, что несколько удлиняет вычисления.SO = h = 4, SA = l = 5, AC = 2r = ? l 2 = r 2 + h 2; 52 = r 2 + 42; 52 − 42 = r 2 или r 2 = 52 − 42 = 25 − 16 = 9; r 2 = 9; r = 3; AC = 2r = 2×3 = 6.

Ответ: 6

Задача 3

Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.

Решение

См. пояснения к предыдущим задачам.AC = 2r = 6, SA = l = 5, SO = h = ? l 2 = r 2 + h 2; r = 6/2 = 3; 52 = 32 + h 2; 52 − 32 = h 2 или h 2 = 52 − 32 = 25 − 9 = 16; h 2 = 16; h = 4.

Ответ: 4

Cookie файлы бывают различных типов:

Необходимые. Эти файлы нужны для обеспечения правильной работы сайта, использования его функций. Отключение использования таких файлов приведет к падению производительности сайта, невозможности использовать его компоненты и сервисы.

Файлы cookie, относящиеся к производительности, эффективности и аналитике. Данные файлы позволяют анализировать взаимодействие посетителей с сайтом, оптимизировать содержание сайта, измерять эффективность рекламных кампаний, предоставляя информацию о количестве посетителей сайта, времени его использования, возникающих ошибках.

Рекламные файлы cookie определяют, какие сайты Вы посещали и как часто, какие ссылки Вы выбирали, что позволяет показывать Вам рекламные объявления, которые заинтересуют именно Вас.

Электронная почта. Мы также можем использовать технологии, позволяющие отслеживать, открывали ли вы, прочитали или переадресовывали определенные сообщения, отправленные нами на вашу электронную почту. Это необходимо, чтобы сделать наши средства коммуникации более полезными для пользователя. Если вы не желаете, чтобы мы получали сведения об этом, вам нужно аннулировать подписку посредством ссылки «Отписаться» («Unsubscribe»), находящейся внизу соответствующей электронной рассылки.

Сторонние веб-сервисы. Иногда на данном сайте мы используем сторонние веб-сервисы. Например, для отображения тех или иных элементов (изображения, видео, презентации и т. п.), организации опросов и т. п. Как и в случае с кнопками доступа к социальным сетям, мы не можем препятствовать сбору этими сайтами или внешними доменами информации о том, как вы используете содержание сайта.

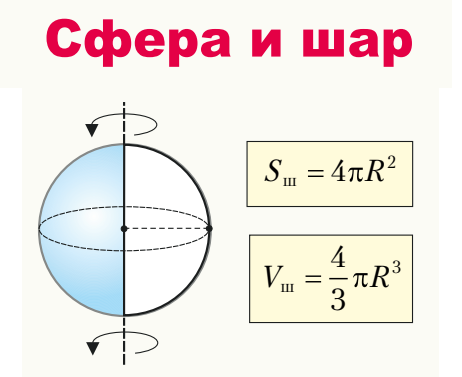
Сфера и шар

10. Сфера — это множество всех точек пространства, равноудаленных от данной точки, называемой центром сферы. Радиусом сферы называется отрезок, соединяющий центр сферы с точкой на сфере, или длина этого отрезка. Хордой сферы называется отрезок, соединяющий две точки на сфере. Диаметр сферы — это хорда, которая проходит через центр сферы. Диаметр сферы равен двум радиусам сферы.

11. Площадь сферы находится по формуле: $S_{сф}=4πR^2$.

12. Шаром называется часть пространства, ограниченная сферой, вместе с самой сферой и ее центром. Данная сфера называется поверхностью шара.
Сечение шара с радиусом $R$ плоскостью, проходящей через центр шара, называется большим кругом шара. Радиус, хорда, диаметр шара те же, что и его сферы.

13. Объем шара находится по формуле $V_{шара}=\frac{4}{3} πR^2$.

Цилиндр

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая L.

Цилиндр называется прямым, если его образующие перпендикулярны основаниям.

Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.

Основные понятия и свойства цилиндра:

Основания цилиндра равны и лежат в параллельных плоскостях.
Все образующие цилиндра параллельны и равны.
Радиусом цилиндра называется радиус его основания ($R$).
Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
Если высоту цилиндра увеличить в $m$ раз, то объем цилиндра увеличится в то же количество раз.
Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.

Пример:

Сосуд в форме цилиндра заполнен водой до отметки $40$ см. Найдите, на какой высоте будет находиться уровень воды, если её перелить в другой сосуд в форме цилиндра, радиус основания которого в $2$ раза больше радиуса основания первого цилиндра. Ответ дайте в сантиметрах.

Решение:

Так как из сосудов перелили одинаковый объем жидкости, следовательно, при равных объемах отличаются радиусы и высоты уровней жидкостей.

$V_1=V_2$;

$R_2=2R_1$, так как у второго цилиндра радиус в два раза больше радиуса первого.

$h_1=40;h_2-?$

Распишем объемы занимаемой жидкости в обоих сосудах и приравняем формулы друг к другу.

$V_1=πR_1^2·h_1=πR_1^2·40$;

$V_2=πR_2^2·h_2=π(2R_1)^2·h_2=4πR_1^2·h_2$.

$πR_1^2·40=4πR_1^2·h_2$

Получили уравнение, которое можно разделить на $πR_1^2$

$40=4 h_2$

Чтобы найти $h_2$ надо сорок разделить на четыре

$h_2=10$

Ответ: $10$

Площадь поверхности и объем цилиндра

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

$S_{бок.пов.}=2πR·h$

Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.

$S_{полн.пов.}=2πR^2+2πR·h=2πR(R+h)$

Объем цилиндра равен произведению площади основания на высоту.

$V= πR^2· h$

Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Составной цилиндр:

Чтобы найти объем составного цилиндра надо:

Разделить составной цилиндр на несколько цилиндров или частей цилиндра.
Найти объем каждого цилиндра.
Сложить объемы.

Сечения цилиндра

Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью. Если сечение проходит через то такое сечение называют осевым сечением цилиндра (рис. 3).

Рис.3

На рисунке 3 изображено одно из осевых сечений цилиндра – AA₁B₁B .

Замечание 4. Каждое с r и h является со сторонами 2r и h .

Определение 3. Перпендикулярным сечением цилиндра называют , перпендикулярное (рис. 4).

Рис.4

Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .

Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».

Объем цилиндра. Площадь боковой поверхности цилиндра.Площадь полной поверхности цилиндра

Для цилиндра с r и h (рис. 5)

Рис.5

введем следующие обозначения

V	объем цилиндра
S_бок	площадь
S_полн	площадь
S_осн	площадь

Тогда справедливы следующие формулы для вычисления объема, площади :

S_осн = πr2,

V = S_оснh = πr2h,

S_бок= 2πrh,

S_полн = 2πr2 + 2πrh == 2π(r + h).

Замечание 7. Формула объема цилиндра V = πr2h может быть получена из

при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.