Определение цилиндра как геометрической фигуры
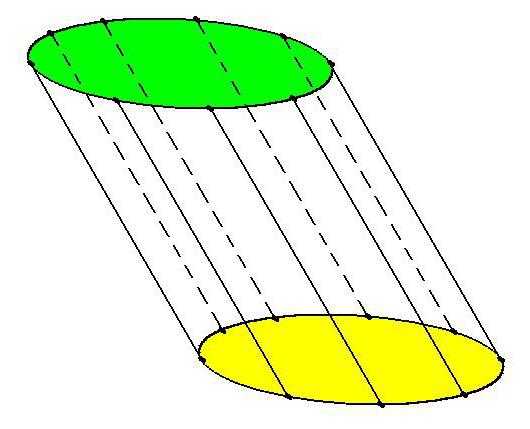
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.
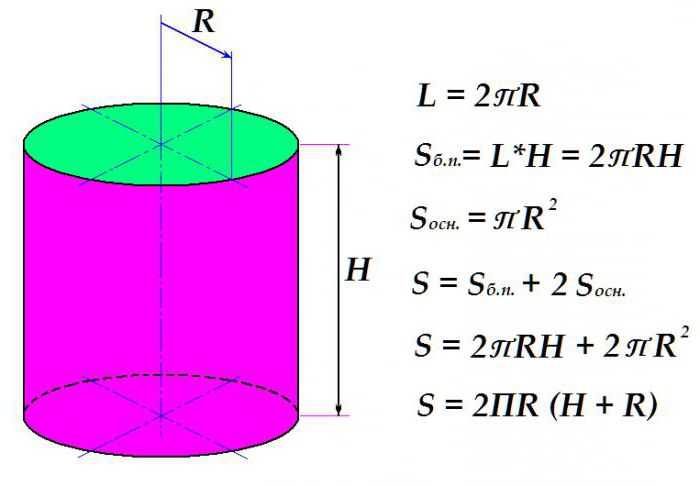
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П
на радиус окружности.
Площадь круга, как известно, равняется произведению П
на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
Задачи на давление жидкостей и газов с ответами и решениями
Формулы, используемые на уроках «Задачи на давление жидкостей и газов».
|
(зависит от условия задачи) |
Задача № 1.
Определить давление бензина на дно цистерны, если высота столба бензина 2,4 м, а его плотность 710 кг/м3.
ОТВЕТ: 17,04 кПа.
Задача № 2.
Какая жидкость находится в сосуде, если столб высотой 0,3 м оказывает давление 5400 Па ?
ОТВЕТ: Серная кислота (1800 кг/м3).
Задача № 3.
Плотность спирта 800 кг/м3. Какова будет высота столба спирта при давлении 2,4 кПа?
ОТВЕТ: 0,3 м. Чтобы увидеть решение, нажмите на спойлер ниже.
Задача № 4.
В цилиндре с маслом на поршень действует сила 40 Н. Чему равна сила давления на внутреннюю поверхность цилиндра площадью 8 дм2? Площадь поршня 2,5 см2. Вес масла не учитывайте.
ОТВЕТ: 12,8 кН.
Задача № 5.
Вычислите давление и силу давления керосина на дно бака площадью 50 дм2, если высота столба керосина в баке 40 см.
ОТВЕТ: 3200 Па; 1600 Н.
Задача № 6.
В мензурку, площадь дна которой 20 см2, налита вода до высоты 10 см. Сколько граммов воды налито? Чему равно давление воды на дно мензурки?
ОТВЕТ: 200 г; 980 Па.
Задача № 7.
Рыба камбала находится на глубине 1200 м и имеет площадь поверхности 560 см2. С какой силой она сдавливается водой?
ОТВЕТ: 678 кН.
Задача № 8.
На какой глубине давление воды в море равно 412 кПа?
ОТВЕТ: 40 м.
Задача № 9.
Поршневой насос может произвести давление 5 • 105 Па. На какую высоту можно поднять воду этим насосом?
ОТВЕТ: 51 м.
Задача № 10.
В сталелитейном производстве «изложницей» называется чугунный стакан без дна, в который выливают расплавленный металл. Верхнее отверстие изложницы немного меньше нижнего для того, чтобы можно было изложницу снять с отвердевшего слитка, когда остынет металл. Чтобы металл снизу не выливался, изложницы ставят на плоское основание и делают их очень массивными. На рисунке слева изображена изложница, справа — подъем изложницы с отлитого слитка. Определите силу давления, которую производит на подложку изложницы налитый чугун, если высота изложницы 1,5 м, а площадь нижнего основания 1600 см2. Плотность чугуна 7000 кг/м3.
ОТВЕТ: 17 кН.
Задача № 11.
Как велика должна быть высота столба ртути и столба спирта, если этот столб производит давление в 105 Па?
ОТВЕТ: высота столба ртути = 0,75 м, высота столба спирта = 12,76 м.
Задача № 12.
Батискаф опустился в море на глубину 50 м. Каково давление на поверхность батискафа на данной глубине? (Плотность морской воды 1010 кг/м3.)
ОТВЕТ: 606 кПа.
Задача № 13.
Человек стоит на кожаном мешке с водой. Рассчитайте, на какую высоту поднимается вода в трубке, если масса человека 75 кг, площадь соприкасающейся с мешком поверхности платформы 1000 см2.
ОТВЕТ: 0,75 м.
Задача № 14 (повышенной сложности).
Брусок массой m = 2 кг имеет форму параллелепипеда. Лежа на одной из граней, он оказывает давление p1 = 1 кПа, лежа на другой — давление 2 кПа, стоя на третьей — давление 4 кПа. Каковы размеры бруска?
ОТВЕТ: 5 см, 10 см, 20 см.
Указание к РЕШЕНИЮ. Обозначим размеры бруска а, b, с, где а > b > с. Тогда из условия следует, что b = а/2, с = а/4, p1 = mg/(ab) = 2mg/a2. Отсюда , а = 20 см, b = 10 см, c = 5 см.
Задача № 15 (олимпиадный уровень).
Оцените массу атмосферы Земли (радиус Земли R = 6400 км)
ОТВЕТ: примерно 5 • 1018 кг.
Указание к РЕШЕНИЮ. Вес атмосферы равен силе давления воздуха на всю поверхность Земли, площадь которой S = 4πR2. Следовательно, mg = ра • 4πR2, где ра = 105 Па — атмосферное давление. Отсюда m = 4πR2 ра /g = 5 • 1018 кг. Эта величина составляет менее одной миллионной части полной массы нашей планеты. Такая простая оценка массы атмосферы возможна потому, что основная часть атмосферы сосредоточена на высотах, малых по сравнению с радиусом Земли. Поэтому можно считать, что вес атмосферы равен mg, где g — ускорение свободного падения вблизи поверхности Земли.
Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = ратм + p*g*h
Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.
Вы смотрели конспект урока «Задачи на Давление жидкостей с ответами и решениями». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Давление твердых тел с ответами и решениями.
- Перейти к теме: ЗАДАЧИ на Сообщающиеся сосуды и гидравлический пресс с решениями.
- Вернуться к Списку конспектов по физике для 7-11 классов
- Найти конспект через Кодификатор ОГЭ по физике
- Найти конспект через Кодификатор ЕГЭ по физике
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.

Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П
на радиус окружности.
Площадь круга, как известно, равняется произведению П
на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.
Что такое поверхность вращения
Прямой круговой цилиндр, без сомнения — самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.
Допустим, имеется некая прямая a
, расположенная вертикально. ABCD — прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a
. Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения — прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.
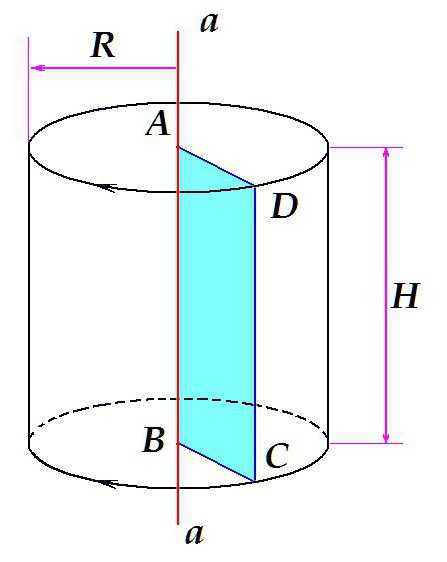
В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг — шар и т.д.
Слайд 5Вклад Евклида в математику.О Евклиде почти ничего неизвестно, откуда он был
родом, где и у кого учился.Папп Александрийский (III в.) сообщает, что он был очень доброжелателен ко всем тем, кто сделал хоть какой-нибудь вклад в математику, корректен, в высшей степени порядочен и совершенно лишен тщеславия. Евклид, как и другие великие греческие геометры, занимался астрономией, оптикой и теорией музыки. До нас дошли его сочинения, посвященные прикладным вопросам: «Феномены» (элементарная сферическая астрономия), «Оптика» (учение о перспективе) и «Сечение канона» ( теория музыки). Это были первые прообразы будущих исследований по математической физике: в них теория выводилась строго дедуктивно из явно сформулированных физических гипотез и математических постулатов. Гораздо больше мы знаем о математическом творчестве Евклида. Прежде всего Евклид является для нас автором «Начал», по которым учились математики всего мира. Эта удивительная книга пережила более двух тысячелетии, но до сих пор не утратила своего значения не только в истории науки, но и самой математике. Созданная там система евклидовой геометрии и теперь изучается во всех школах мира и лежит в основе почти всей практической деятельности людей. На геометрии Евклида базируется классическая механика, ее апофеозом было появление в 1687 г. Математических начал натуральной философии Ньютона, где законы земной и небесной механики и физики устанавливаются в абсолютном евклидовом пространстве. Содержание «Начал» далеко не исчерпывается элементарной геометрией — это основы всей античной математики. Здесь подводится итог более чем 300-летнему ее развитию и вместе с тем создается прочная 6aзa для дальнейших исследований. Последующие математики ссылались на предложения «Начал», как на нечто окончательно установленное.
Слайд 6Вклад Кавальери в математику.
В своем основном труде «Геометрия» (1635г.) Кавальери развил разработанный им задолго до выхода книги новый метод определения площадей и объемов – так называемый метод неделимых. Неделимыми Кавальери называл параллельные между собой хорды плоской фигуры или параллельные плоскости тела. Важнейший признак неделимости состоит в том, что число измерений его на единицу меньше самого геометрического образа. У плоской фигуры 2 измерения, у ее неделимого, т.е. у отрезка – 1 измерение. Кавальери доказал теорему о том, что площади двух подобных фигур относятся как квадраты, а объемы – как кубы соответствующих неделимых, и установил, что отношение суммы квадратов всех неделимых треугольника к сумме квадратов всех неделимых параллелограмма, имеющего с треугольником одинаковые основания и высоту, равно 1:3. Впоследствии Кавальери нашел аналогичные соотношения для суммы кубов и т.д. до девятой степени неделимых. Труды Кавальери сыграли огромную роль в формировании исчисления бесконечно малых.
Слайд 49В него входят: помощь при сердечно-сосудистых заболеваниях, нейротрофических заболеваниях, гипертонии, болезнях
выводящих путей, астме, бессоннице, головных болях, а также в качестве средства для снятия стрессов и профилактике атеросклероза. Одна из удивительных особенностей Цилиндров Фараона — улучшение работы практически всех основных систем организма (показатели работы этих систем улучшаются в среднем в 2 — 2.5 раза).Согласно мнению ряда врачей, Цилиндры Фараона представляют собой уникальный, самонастраивающийся на каждого человека, физиотерапевтический прибор, созданный гением древнеегипетских ученых. Их целебные свойства, включающие в себя металлотерапию, гальванотерапию и магнитотерапию позволили врачу-биоэнергетику Т.Мешковой разработать эффективную методику использования Цилиндров. Цилиндры Фараона полезны как взрослым людям, так и детям. Они создают в организме человека обстановку, при которой ему гораздо легче справляться со своими бедами. Цилиндры — прекраснее профилактическое средство против ряда болезней. Согласно результатам экспериментов врача Т.Мешковой, Цилиндры Фараона защищают от воздействия излучений различной электронной техники: компьютеров, телевизоров, микроволновых печей и т.д.
Примечания
Wikimedia Foundation
.
2010
.
Синонимы
Смотреть что такое «Цилиндр» в других словарях:
— (лат. cylindrus) 1) геометрическое тело, ограниченное с концов двумя кругами, с боков плоскостью, огибающею эти круги. 2) в часовом мастерстве: особого рода рычаг двойного колеса. 3) шляпа, имеющая форму цилиндра. Словарь иностранных слов,… … Словарь иностранных слов русского языка
цилиндр
— а, м. cylindre m., нем. Zylinder <, лат. cylindrus <гр. 1. Геометрическое тело, образуемое вращение прямоугольника вокруг одной из его сторон. Объем цилиндра. БАС 1. Толстота цилиндра равна площади его основанья, помноженной на высоту. Даль … Исторический словарь галлицизмов русского языка
Муж., греч. прямая стопка, вал; облец, обляк; тело, ограниченное с концов двумя кругами, а с боков гнутою по кругам плоскостью. Толстота цилиндра равна площади его основанья, помноженной на высоту, геом. Паровой цилиндр, халява, труба, в которой… … Толковый словарь Даля
— высокая мужская шляпа из шелкового плюша с небольшими твердыми полями … Большой Энциклопедический словарь
ЦИЛИНДР, твердое тело или поверхность, образуемые вращением прямоугольника вокруг одной из его сторон в качестве оси. Объем цилиндра, если обозначить его высоту как h, а радиус основания как r, равен pr2h, а площадь изогнутой поверхности 2prh … Научно-технический энциклопедический словарь
ЦИЛИНДР, цилиндра, муж. (от греч. kylindros). 1. Геометрическое тело, образуемое вращением прямоугольника около одной из его сторон, называемой осью, и имеющее в основаниях круг (мат.). 2. Часть машин (двигателей, насосов, компрессоров и т.д.) в… … Толковый словарь Ушакова
ЦИЛИНДР, а, муж. 1. Геометрическое тело, образованное вращением прямоугольника вокруг одной из его сторон. 2. Колонновидный предмет, напр. часть поршневой машины. 3. Высокая твёрдая шляпа такой формы с небольшими полями. Чёрный ц. | прил.… … Толковый словарь Ожегова
— (Steam cylinder) одна из основных деталей поршневых машин. Выполняется в виде полого круглого Ц., в котором движется поршень. Ц. паровых машин снабжается обычно паровой рубашкой для обогревания его стенок в целях уменьшения конденсации пара.… … Морской словарь
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.

Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.

Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П
на радиус окружности.
Площадь круга, как известно, равняется произведению П
на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Слайд 42Винтовые линии бывают правовинтовые и левовинтовые.Предположим, что по винтовой линии движется
точка. Проекцией винтовой линии на плоскость, перпендикулярную кеё оси (будем называть осью винтовой линии ось цилиндра, на котором она расположена), будет, очевидно, окружность. Поэтому если смотреть на винтовую линию в направлении её оси, то будет казаться, что точка движется по окружности. Если точка движется по окружности по часовой стрелке, удаляясь от нас, то винтовая линия называется право- винтовой, если же она движется по часовой стрелке, приближаясь к нам, то винтовая линия называется левовин- товой. Правовинтовую и левовинтовую линии на одном итом же цилиндре с одинаковым углом подъёма совместить нельзя. На черт.1 у нас получилась левовинтовая линия; чтобы получить правовинтовую линию, нужно наматывать треугольник в противоположном направлении.
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.
Цилиндр
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая L.
Цилиндр называется прямым, если его образующие перпендикулярны основаниям.
Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.
Основные понятия и свойства цилиндра:
- Основания цилиндра равны и лежат в параллельных плоскостях.
- Все образующие цилиндра параллельны и равны.
- Радиусом цилиндра называется радиус его основания ($R$).
- Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
- Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
- Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
- Если высоту цилиндра увеличить в $m$ раз, то объем цилиндра увеличится в то же количество раз.
- Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
- Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
Пример:
Сосуд в форме цилиндра заполнен водой до отметки $40$ см. Найдите, на какой высоте будет находиться уровень воды, если её перелить в другой сосуд в форме цилиндра, радиус основания которого в $2$ раза больше радиуса основания первого цилиндра. Ответ дайте в сантиметрах.
Решение:
Так как из сосудов перелили одинаковый объем жидкости, следовательно, при равных объемах отличаются радиусы и высоты уровней жидкостей.
$V_1=V_2$;
$R_2=2R_1$, так как у второго цилиндра радиус в два раза больше радиуса первого.
$h_1=40;h_2-?$
Распишем объемы занимаемой жидкости в обоих сосудах и приравняем формулы друг к другу.
$V_1=πR_1^2·h_1=πR_1^2·40$;
$V_2=πR_2^2·h_2=π(2R_1)^2·h_2=4πR_1^2·h_2$.
$πR_1^2·40=4πR_1^2·h_2$
Получили уравнение, которое можно разделить на $πR_1^2$
$40=4 h_2$
Чтобы найти $h_2$ надо сорок разделить на четыре
$h_2=10$
Ответ: $10$
Площадь поверхности и объем цилиндра
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.
$S_{бок.пов.}=2πR·h$
Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.
$S_{полн.пов.}=2πR^2+2πR·h=2πR(R+h)$
Объем цилиндра равен произведению площади основания на высоту.
$V= πR^2· h$
Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Составной цилиндр:
Чтобы найти объем составного цилиндра надо:
- Разделить составной цилиндр на несколько цилиндров или частей цилиндра.
- Найти объем каждого цилиндра.
- Сложить объемы.
Слайд 53С примерами винтовой линии мы часто встречаемся в физике и технике.
Форму винтовой линии с очень малым углом имеет каждый слой проволоки в индукционной катушке. При равномерной подаче резец токарного станка при обточке цилиндра оставляет на этом цилиндре след в виде винтовой линии. Форму винтовой линии имеет режущая кромка цилиндрических спиральных свёрл. Форма нарезки на всякого рода скрепляющих, регулировочных винтах, болтах и гайках — винтовая линия (причём, как правило, применяется правовинтовая нарезка). При прямолинейном равномерном полёте точка на пропеллере самолёта описывает винтовую линию. Точно так же винтовую линию описывает точка на гребном винте как океанского парохода, так и моторной лодки. Форму винтовой линии имеет штопор, употребляемый для раскупоривания бутылок. Винтовую линию описывает точка крыла самолёта, когда он «входит в штопор». При прямолинейном равномерном полёте винтовочной пули, а также артиллерийского снаряда точки на их поверхности описывают винтовые линии. Во всех перечисленных примерах научно-технического характера при производимых расчётах используются те или иные свойства винтовой линии. Число и характер приведённых примеров говорят о важных практических применениях винтовой линии.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.
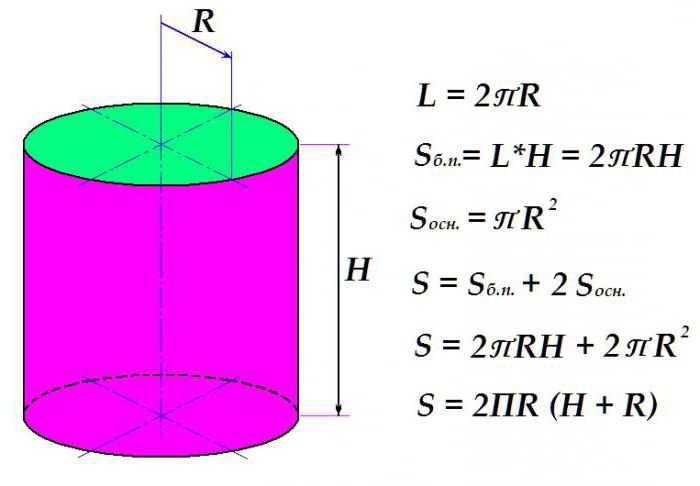
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П
на радиус окружности.
Площадь круга, как известно, равняется произведению П
на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.

Слайд 48Цилиндры Фараона — два загадочных предмета цилиндрической формы в руках некоторых
древнеегипетских изваяний. Среди специалистов-египтологов не существует единого мнения о происхождении данных предметов. В 1976 году в Закавказье Р.Добровольским и В.Ковтуном была обнаружена старинная эзотерическая рукопись под названием «Тайны Жизни и Смерти», в которой содержалась информация о Лунном и Солнечном цилиндрах, изготовленных из цинка и меди с определенным внутренним наполнением. По утверждению неизвестного автора Цилиндры Фараона использовались фараонами и жрецами Древнего Египта для укрепления жизненных сил и общения с богами. Цилиндры Фараона были воссозданы согласно древнему рецепту и затем в течение многих лет исследовались физиком Владимиром Ковтуном. В этих исследованиях принимали участие медики, физики, египтологи, экстрасенсы и парапсихологи. Результаты исследований поразили ученых. Оказалось, что Цилиндры Фараона обладают широчайшим спектром благотворного воздействия на организм человека.

Определение объёма фигуры
Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.
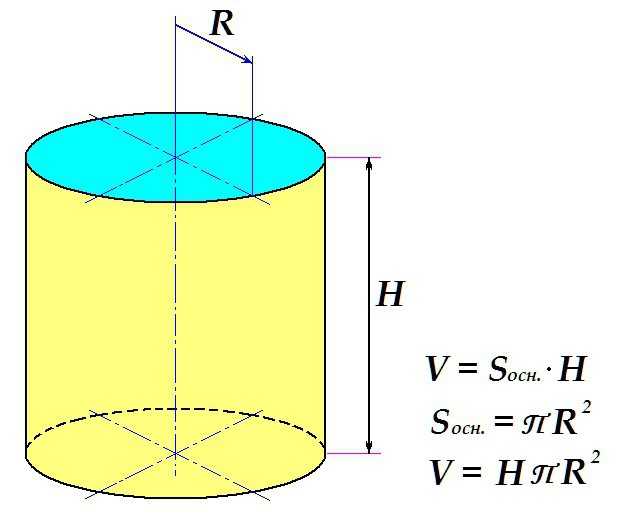
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П
и на квадрат радиуса основания.
Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.
Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N
. Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.
Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.
Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.
Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями — перпендикулярный отрезок, построенный между ними.

Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.
Что такое поверхность вращения
Прямой круговой цилиндр, без сомнения — самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.
Допустим, имеется некая прямая a
, расположенная вертикально. ABCD — прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a
. Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения — прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.
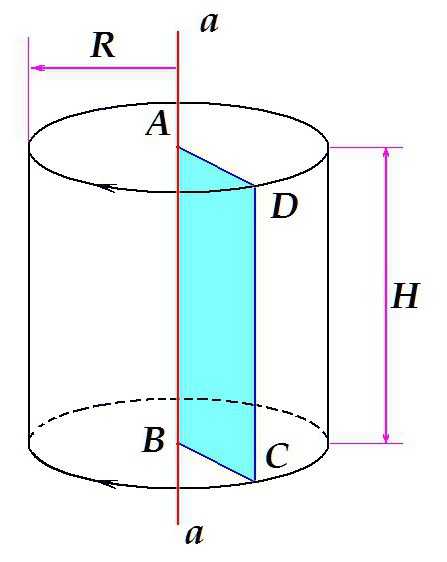
В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг — шар и т.д.





























