Как называть цилиндры в геометрии буквами

Площадь развертки цилиндра

Выше мы показали, как можно получить развертку фигуры. Чтобы рассчитать ее площадь, необходимо сложить площади для всех ее частей, то есть для двух круглых оснований и одного прямоугольника.

Обозначим радиус основания буквой r, а высоту фигуры — буквой h. Площадь одного основания равна площади круга, то есть:

S_o = pi*r2

Здесь pi — число Пи, приблизительно равное 3,14.

Чтобы вычислить площадь прямоугольника, представляющего боковую поверхность фигуры в развернутом виде, необходимо знать две его стороны. Одна из них равна высоте h. Вторая, как можно догадаться, соответствует длине директрисы, то есть длине окружности. Обозначим ее l. Тогда можно записать следующие равенства:

l = 2*pi*r;

S_b = l*h = 2*pi*r*h

Здесь S_b — площадь прямоугольника, равная площади цилиндрической поверхности.

Учитывая, что фигура имеет два основания, складываем рассчитанные величины, получаем общую площадь развертки цилиндра:

S = 2*S_o + S_b = 2*pi*r2 + 2*pi*r*h = 2*pi*r*(r + h)

Площадь S фигуры однозначно определяется через ее радиус и высоту.

Покажем, как использовать это равенство для решения геометрической задачи.

Задача 3.

Высота цилиндра 6см, радиус основания 5см.

Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4см от нее.

Дано: Н = 6см, R = 5см, ОЕ = 4см.

Найти: S сеч.

S сеч.
= КМ×КС,

ОЕ = 4 см, КС = 6 см.

Треугольник ОКМ − равнобедренный (ОК = ОМ = R = 5 см),

треугольник ОЕК − прямоугольный.

Из треугольника ОЕК, по теореме Пифагора:

КМ = 2ЕК = 2×3 = 6,

S сеч.
= 6×6 = 36 см 2
.

Цель данного реферата выполнена, рассмотрено такое геометрическое тело, как цилиндр.

Рассмотрены следующие задачи:

− дано определение цилиндра;

− рассмотрены элементы цилиндра;

− изучены свойства цилиндра;

− рассмотрены виды сечения цилиндра;

− выведена формула площади цилиндра;

− выведена формула объема цилиндра;

− решены задачи с использованием цилиндра.

1. Погорелов А. В. Геометрия: Учебник для 10 – 11 классов общеобразовательных учреждений, 1995.

2. Бескин Л.Н. Стереометрия. Пособие для учителей средней школы, 1999.

3. Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Киселева Л. С., Позняк Э. Г. Геометрия: Учебник для 10 – 11 классов общеобразовательных учреждений, 2000.

4. Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия: учебник для 10-11 классов общеобразовательных учреждений, 1998.

5. Киселев А. П., Рыбкин Н. А. Геометрия: Стереометрия: 10 – 11 классы: Учебник и задачник, 2000.

Представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.

Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:

Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы. Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру. Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.

Объем прямого цилиндра

Объем прямого цилиндра равен произведению площади его основания на высоту

где Q — площадь основания, а Н — высота цилиндра.

Так как площадь основания цилиндра равна Q, то существуют последовательности описанных и вписанных многоугольников с площадями Q n
и Q’ n
таких, что

\(\lim_{n \rightarrow \infty}\) Q n
= \(\lim_{n \rightarrow \infty}\) Q’ n
= Q.

Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H. Эти призмы являются описанными и вписанными для данного цилиндра. Их объемы находятся по формулам

V n
= Q n
H и V’ n
= Q’ n
H.

Следовательно,

V= \(\lim_{n \rightarrow \infty}\) Q n
H = \(\lim_{n \rightarrow \infty}\) Q’ n
H = QH.

Следствие.

Объем прямого кругового цилиндра вычисляется по формуле

V = π R 2 H

где R — радиус основания, а H — высота цилиндра.

Так как основание кругового цилиндра есть круг радиуса R, то Q = π R 2 , и поэтому

Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.

Планиметрия — раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье — цилиндр.

Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже — коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец — знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.

ГЕОМЕТРИЯ: Стереометрия

20. Цилиндр и конус

Поверхность вращения.

Поверхностью вращения называется поверхность, которая получается при вращении какой-нибудь линии, называющейся образующей, вокруг неподвижной прямой, называющейся осью; при этом предполагается, что образующая при своём вращении неизменно связана с осью.

Всякая секущая плоскость, проходящая через ось, называется меридиональной плоскостью, а пересечение её с поверхностью вращения — меридианом

Цилиндр.

Цилиндрической поверхностьюобразующейнаправляющую

Цилиндром называется тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями. Часть цилиндрической поверхности, заключённая между плоскостями, называется боковой поверхностью, а части плоскостей, отсекаемые этой поверхностью, — основаниями цилиндра. Расстояние между основаниями есть высота цилиндра. Цилиндр называется прямым или наклонным, смотря по тому, будут ли его образующие перпендикулярны или наклонны к основаниям.

Прямой цилиндр называется круговым, если его основания — круги. В элементарной геометрии рассматривается только прямой круговой цилиндр; для краткости его называют просто цилиндром

Иногда приходится рассматривать такие призмы, основания которых суть многоугольники, вписанные в основания цилиндра или описанные около них; такие призмы называются вписанными в цилиндр или описанными около него.

Конус.

Конической поверхностьюобразующейвершинунаправляющую

Конусом называется тело, ограниченное замкнутой конической поверхностью и плоскостью, пересекающей все образующие по одну сторону от вершины. Часть конической поверхности, ограниченная этой плоскостью, называется боковой поверхностью, а часть плоскости, отсекаемая этой поверхностью, — основанием конуса. Перпендикуляр, опущенный из вершины на основание, есть высота конуса.

Конус называется прямым круговым, если его основание — круг, а высота проходит через центр основания. В элементарной геометрии рассматривается только прямой круговой конус; для краткости его называют просто конусом

Усечённым конусом

Поверхность цилиндра и конуса.

За величину боковой поверхности цилиндра принимается предел, к которому стремится боковая поверхность вписанной в этот цилиндр правильной призмы, когда число её боковых граней неограниченно удваивается.

За величину боковой поверхности конуса принимается предел, к которому стремится боковая поверхность вписанной в этот конус правильной пирамиды, когда число её боковых граней неограниченно удваивается.

Теорема: Боковая поверхность цилиндра равна произведению длины окружности основания на высоту.

Теорема: Боковая поверхность конуса равна произведению длины окружности основания на половину образующей.

Теорема: Боковая поверхность усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую.

Объёмы цилиндра и конуса.

За величину объёма цилиндра принимается предел, к которому стремится объём вписанной в этот цилиндр правильной призмы, когда число её боковых граней неограниченно удваивается.

За величину объёма конуса принимается предел, к которому стремится объём вписанной в этот конус правильной пирамиды, когда число её боковых граней неограниченно удваивается.

Теорема: Объём цилиндра равен произведению площади основания на высоту.

Теорема: Объём конуса равен произведению площади основания на треть высоты.

Подобные цилиндры и конусы.

Два цилиндра или конуса называются подобными, если они образуются при вращении подобных прямоугольников или треугольников вокруг сходственных сторон.

Теорема: Боковые и полные поверхности подобных цилиндров или конусов относятся как квадраты радиусов или высот, а объёмы — как кубы радиусов или высот.

Цилиндр как фигура геометрии

Предположим, что у нас имеется некоторая плавная кривая. Это может быть круг, эллипс, парабола и так далее. Возьмем отрезок произвольной длины, который не лежит в плоскости кривой, и опишем с помощью него поверхность, следуя направлению кривой и транслируя отрезок параллельно самому себе. Полученная поверхность называется цилиндрической или просто цилиндром. Отмеченная кривая называется директрисой (направляющей), а отрезок — генератрисой (образующей).

Если к цилиндрической поверхности добавить еще две плоские одинаковые фигуры, ограничивающие эту поверхность с торцов, то полученное тело также называется цилиндром. Оно состоит из двух равных оснований и цилиндрической поверхности.

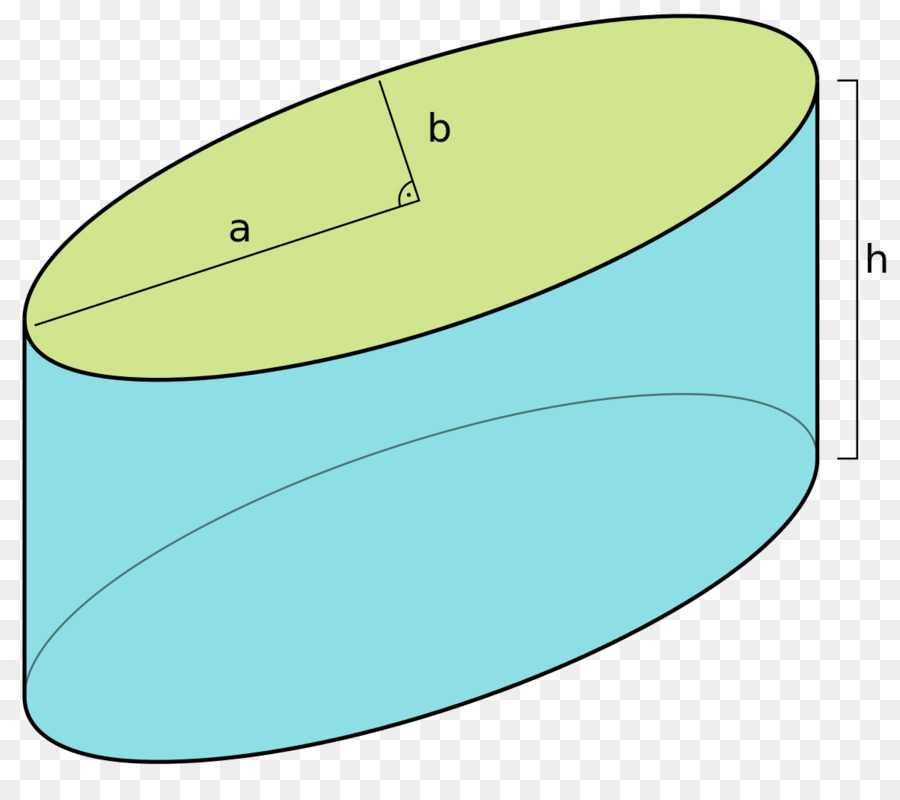
Для наглядного представления описанной фигуры ниже приведен рисунок. На нем изображен эллиптический цилиндр, имеющий полуоси a и b и высоту h (дистанция между основаниями).

Как правильно штриховать цилиндр

В мастер-классе выше мы с вами увидели, как рисуется цилиндр в объеме, и как сделать этот цилиндр со штриховкой правильно. Теперь давайте более детально распишем, какой должна быть штриховка.

• Рефлекс – тон, похожий на полутень, располагается у краев предмета
• Блик – самая светлая часть рисунка, ее мы не трогаем карандашом, а наоборот, высветляем ластиком
• Полутень – основной тон в штриховке
• Светотень – распределение света и тени на рисунке

Представьте себе блик – яркое световое пятно на предмете. И вот этот свет от блика должен как-то расходиться по всей поверхности рисуемого вами предмета. Это и будет полутень.

Если вы сомневаетесь, в правильности своей работы, то вам нужно отойти на небольшое расстояние от рисунка и посмотреть на него со стороны. Как правило, при таком рассмотрении вы сразу заметите погрешности в объеме, тенях и пропорциях.

После нее, у вас будет гораздо меньше вопросов о штриховке и все получится уже с первого раза.

1.5. Объем цилиндра

Если
геометрическое тело простое, то есть допускает разбиение на конечное число
треугольных пирамид, то его объем равен сумме объемов этих пирамид. Для
произвольного тела объем определяется следующим образом.

Данное тело имеет
объем V, если существует содержащие его простые тела и содержащиеся в нем
простые тела с объемами, сколько угодно мало отличающимися от V.

Применим это
определение к нахождению объема цилиндра с радиусом основания R и высотой Н.

При выводе
формулы для площади круга были построены такие два n-угольника (один −
содержащий круг, другой − содержащийся в круге), что их площади при
неограниченном увеличении n неограниченно приближались к площади круга.
Построим такие многоугольники для круга в основании цилиндра. Пусть Р −
многоугольник, содержащий круг, а Р’ − многоугольник, содержащийся в
круге (рис. 6).

Рис. 7 −
Цилиндр с описанной и вписанной в него призмой

Построим две
прямые призмы с основаниями Р и Р’ и высотой Н, равной высоте цилиндра. Первая
призма содержит цилиндр, а вторая призма содержится в цилиндре. Так как при
неограниченном увеличении n площади оснований призм неограниченно приближаются
к площади основания цилиндра S, то их объемы неограниченно приближаются к SН.
Согласно определению объем цилиндра

V = SH = πR2H.

Итак, объем
цилиндра равен произведению площади основания на высоту.

Слайд 6Вклад Кавальери в математику.

В своем основном труде «Геометрия» (1635г.) Кавальери развил разработанный им задолго до выхода книги новый метод определения площадей и объемов – так называемый метод неделимых. Неделимыми Кавальери называл параллельные между собой хорды плоской фигуры или параллельные плоскости тела. Важнейший признак неделимости состоит в том, что число измерений его на единицу меньше самого геометрического образа. У плоской фигуры 2 измерения, у ее неделимого, т.е. у отрезка – 1 измерение. Кавальери доказал теорему о том, что площади двух подобных фигур относятся как квадраты, а объемы – как кубы соответствующих неделимых, и установил, что отношение суммы квадратов всех неделимых треугольника к сумме квадратов всех неделимых параллелограмма, имеющего с треугольником одинаковые основания и высоту, равно 1:3. Впоследствии Кавальери нашел аналогичные соотношения для суммы кубов и т.д. до девятой степени неделимых. Труды Кавальери сыграли огромную роль в формировании исчисления бесконечно малых.

3. Сечения цилиндра

Сечение цилиндра
плоскостью, параллельной его оси, представляет собой прямоугольник (рис. 3, а).
Две его стороны − образующие цилиндра, а две другие − параллельные
хорды оснований.

а)                б)

    в)                   г) 

Рис. 3 – Сечения
цилиндра

В частности,
прямоугольником является осевое сечение. Это − сечение  цилиндра
плоскостью, проходящей через его ось (рис. 3, б).

 Сечение цилиндра
плоскостью, параллельной основанию − круг (рис 3,  в).

Сечение цилиндра
плоскостью не параллельной основанию и его оси − овал  (рис. 3г).

Доказательство.
Пусть β − плоскость, параллельная плоскости основания цилиндра.
Параллельный перенос в направлении оси цилиндра, совмещающий плоскость β с
плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью
β с окружностью основания. Теорема доказана.  

Площадь
боковой поверхности цилиндра.

За площадь боковой
поверхности цилиндра принимается предел, к которому стремится площадь боковой
поверхности правильной призмы, вписанной в цилиндр, когда число сторон
основания этой призмы неограниченно возрастет.

Теорема 2.
Площадь боковой поверхности цилиндра равна произведению длины окружности его
основания на высоту (S_бок.ц = 2πRH, где R − радиус
основания цилиндра, Н − высота цилиндра).

а)          б)   
Рис. 4 − Площадь
боковой поверхности цилиндра

 Доказательство.

Пусть P_nи Н соответственно периметр основания
и высота правильной n-угольной призмы, вписанной в цилиндр (рис. 4, а). Тогда
площадь боковой поверхности этой призмы S_бок.ц − P_nH. Предположим, что число сторон
многоугольника, вписанного в основание, неограниченно растет (рис. 4, б). Тогда
периметр P_n стремится к длине окружности С = 2πR,
где R— радиус основания цилиндра, а высота H не изменяется. Таким образом,
площадь боковой поверхности призмы стремится к пределу 2πRH,
т. е. площадь боковой
поверхности цилиндра равна S_бок.ц = 2πRH.
Теорема доказана.

Площадь полной
поверхности цилиндра.

Площадью полной
поверхности цилиндра называется сумма площадей боковой поверхности и двух
оснований. Площадь каждого основания цилиндра равна πR2,
следовательно, площадь полной   поверхности  
цилиндра  S_полн вычисляется  
по   формуле S_бок.ц = 2πRH+ 2πR2.

r

T1

T

F

F1

F

T

F

Рис. 5 − Площадь
полной поверхности цилиндра

Если боковую
поверхность цилиндра разрезать по образующей FT (рис. 5, а) и развернуть так,
чтобы все образующие оказались в одной плоскости, то в результате мы получим
прямоугольник FTT1F1, который называется разверткой боковой поверхности
цилиндра. Сторона FF1 прямоугольника есть развертка окружности основания
цилиндра, следовательно, FF1=2πR, а его сторона FT равна образующей
цилиндра, т. е. FT = Н (рис. 5, б). Таким образом, площадь FT∙FF1=2πRH
развертки цилиндра равна пло­щади его боковой поверхности.

Цилиндр

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая  L.

Цилиндр называется прямым, если его образующие перпендикулярны основаниям.

Осевое сечение цилиндра  — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.

Основные понятия и свойства цилиндра:

1. Основания цилиндра равны и лежат в параллельных плоскостях.
2. Все образующие цилиндра параллельны и равны.
3. Радиусом цилиндра называется радиус его основания ($R$).
4. Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
5. Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
6. Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
7. Если высоту цилиндра увеличить в $m$ раз, то объем цилиндра увеличится в то же количество раз.
8. Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
9. Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.

Пример:

Сосуд в форме цилиндра заполнен водой до отметки $40$ см. Найдите, на какой высоте будет находиться уровень воды, если её перелить в другой сосуд в форме цилиндра, радиус основания которого в $2$ раза больше радиуса основания первого цилиндра. Ответ дайте в сантиметрах.

Решение:

Так как из сосудов перелили одинаковый объем жидкости, следовательно, при равных объемах отличаются радиусы и  высоты уровней жидкостей.

$V_1=V_2$;

$R_2=2R_1$, так как у второго цилиндра радиус в два раза больше радиуса первого.

$h_1=40;h_2-?$

Распишем объемы занимаемой жидкости в обоих сосудах и приравняем формулы друг к другу.

$V_1=πR_1^2·h_1=πR_1^2·40$;

$V_2=πR_2^2·h_2=π(2R_1)^2·h_2=4πR_1^2·h_2$.

$πR_1^2·40=4πR_1^2·h_2$

Получили уравнение, которое можно разделить на $πR_1^2$

$40=4 h_2$

Чтобы найти $h_2$ надо сорок разделить на четыре

$h_2=10$

Ответ: $10$

Площадь поверхности  и объем цилиндра

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

$S_{бок.пов.}=2πR·h$

Площадь поверхности цилиндра равна сумме  двух площадей оснований и площади боковой поверхности.

$S_{полн.пов.}=2πR^2+2πR·h=2πR(R+h)$

Объем цилиндра равен произведению площади основания на высоту.

$V= πR^2· h$

Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Составной цилиндр:

Чтобы найти объем составного цилиндра надо:

1. Разделить составной цилиндр на несколько цилиндров или частей цилиндра.
2. Найти объем каждого цилиндра.
3. Сложить объемы.

Виды цилиндров

1. Прямой цилиндр – имеет одинаковые симметричные основания (круг или эллипс), параллельные друг другу. Отрезок между точками симметрии оснований перпендикулярен им, является осью симметрии и высотой фигуры.
2. Наклонный цилиндр – имеет одинаковые симметричные и параллельные друг другу основания. Но отрезок между точками симметрии не перпендикулярен этим основаниям.
3. Косой (скошенный) цилиндр – основания фигуры не взаимно параллельны.
4. Круговой цилиндр – основаниями является круг. Также выделяют эллиптические, параболические и гиперболические цилиндры.
5. Равносторонний цилиндр – прямой круговой цилиндр, диаметр основания которого равен его высоте.

Сами прямые называют образующими цилиндрической поверхности.
Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.

Так как все образующие и ось перпендикулярны плоскости альфа, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).

Если построить ещё одну плоскость бета, которая будет параллельна плоскости альфа, то отрезки образующих, заключённые между плоскостями альфа и бета будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости бета, дают окружность, равную окружности, лежащей в плоскости альфа.

Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях альфа и бета) называется цилиндром.
Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.

Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.

Сечения цилиндра различными плоскостями

Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого – образующие, а две другие – отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).

Основные формулы

Формула для вычисления площади боковой поверхности цилиндра: Sбок=2пRL.

То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: Sполн=2пR(R+L).

Примеры и разбор решения заданий тренировочного модуля

Дан цилиндр.

Выберите значение площади его боковой поверхности

1. 60π
2. 192π
3. 120π
4. 36π

Решение:

Площадь боковой поверхности вычисляется по формуле: S=2πRL.

R=6, L=10

Подставим: S=2π·6·10=120π.

Ответ: 3) 120π

Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.

Решение:

Sполн=2πR(R+L)

По условию задачи L=R+6.

144π=2πR(R+R+6).

Получили квадратное уравнение относительно радиуса:

R2+6R-72=0

R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.

Ответ: 12.

Задача

Осевое сечение цилиндра – квадрат со стороной 20 см. Найти высоту цилиндра, радиус цилиндра, ось цилиндра и площадь основания цилиндра.

Решение

Одна из сторон осевого сечения – образующая (она же равна оси цилиндра и она же равна высоте). Значит, высота и ось равны 20 см. Далее, вторая сторона осевого сечения – диаметр основания. Он равен 20 см, значит, радиус – 10 см. Наконец, площадь основания ищется по формуле

Итак, ребята, на этом уроке мы изучили, что такое цилиндрическая поверхность, её образующая; цилиндр, все его элементы и сечения; площади поверхностей цилиндра.

Связанные определения[править | править код]

• Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей).
• Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями, ограничивающими цилиндр, называются основаниями этого цилиндра.
• Часть цилиндрической поверхности, находящаяся между плоскостями оснований, называется боковой поверхностью цилиндра.
• Высотой цилиндра называется отрезок, высекаемый плоскостями его оснований на прямой, перпендикулярной им, или длина этого отрезка.

Особенности основания цилиндра

Форма основания

Основание цилиндра — это круг или эллипс в зависимости от его типа (правильный или неправильный). Круг встречается чаще и имеет все свойства круга: радиус, диаметр, длину и площадь окружности. Эллипс имеет два радиуса — большой и малый, а также периметр и площадь, которые вычисляются по специальным формулам.

Положение основания

Основание цилиндра расположено параллельно и на одинаковом расстоянии друг от друга. Это делает все боковые грани цилиндра равными и формирует круглый или овальный цилиндр.

Основание как плоскость

Основание цилиндра рассматривается как плоскость, граничащая на боковую поверхность. Если одно из оснований цилиндра является неправильным многоугольником, то его площадь вычисляется по формулам геометрии этого многоугольника.

Заключение

Основание цилиндра — это база, на которой строится вся фигура. Его особенности, тесно связанные с его формой и положением, определяют характеристики всего цилиндра и его поведение в пространстве.