Чему равна площадь поперечного сечения цилиндра?

Площадь цилиндра — как правильно рассчитать

Определение

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.

Перед тем, как начать вычисление площади цилиндра, необходимо учесть, что существует два ее вида:

1. Полная площадь поверхности цилиндра. Она равна сумме боковой поверхности цилиндра и двойной площади его основания.
2. Площадь боковой поверхности цилиндра. Она равняется произведению высоты цилиндра на длину окружности основания.

Чтобы вычислить общую площадь поверхности цилиндра, нужно применить формулу:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

\(S=2\times\pi\times R\times h+2\times\pi\times R^2=2\times\pi\times R\times\left(h+R\right)\)

Здесь R — радиус окружности, а h — высота. 

Чтобы найти площадь боковой поверхности цилиндра, нужно воспользоваться формулой: 

\(S=2\times\pi\times R\times h\)

Виды цилиндров

Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.

Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.

По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.

Понятие цилиндра

Цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью (боковая поверхность цилиндра) и двумя параллельными плоскостями (основаниями цилиндра).

Основание цилиндра — это круглая плоскость, на которую опирается геометрическая фигура. Таких оснований у цилиндра 2, они абсолютно одинаковы.

Прямая, соединяющая центры оснований, называется осью цилиндра. Плоскость, проходящая через ось будет осевым сечением. Очень часто данное понятие возникает при решении задач ЕГЭ. На рисунке ниже выделено красным пунктиром.

Вся боковая поверхность цилиндра состоит из бесконечного количества прямых, параллельных оси цилиндра. Эти прямые носят название образующих цилиндра. На рисунке выше это AB или KD.

Высотой цилиндра является длина его образующей, а радиус основания — радиусом цилиндра.

Определение и формула расчета

Площадь осевого сечения цилиндра – это площадь плоского сечения, проходящего через ось цилиндра. Она является важным параметром при расчете различных физических и технических задач, связанных с цилиндрами.

Формула для расчета площади осевого сечения цилиндра зависит от его формы. Если цилиндр имеет круглое основание, то площадь осевого сечения можно вычислить с помощью формулы:

S = π * r^2,

где S — площадь осевого сечения цилиндра, π — число π (пи), r — радиус круглого основания.

Если же цилиндр имеет не круглое, а другое основание (например, прямоугольное), то формула для расчета площади осевого сечения будет отличаться.

В случае прямоугольного основания, где a — длина стороны а, b — длина стороны b:

S = a * b

(для прямоугольного основания)

Для других форм основания формула будет соответствующей

Важно помнить, что расчет площади осевого сечения цилиндра должен быть выполнен с учетом формы основания цилиндра

Что такое площадь осевого сечения цилиндра

Площадь осевого сечения цилиндра – это площадь плоскости, которая пересекает цилиндр в направлении, параллельном его оси. Она представляет собой площадь фигуры, образованной сечением цилиндра и включающей сегменты окружностей и между ними.

Обозначается площадь осевого сечения цилиндра через символ S.

Площадь осевого сечения цилиндра является важным параметром, который может быть использован для расчетов и применен в различных областях:

1. In the field of engineering:

   • Расчеты прочности и допусков при разработке конструкций, где цилиндры используются как элементы
   • Планирование и оптимизация трубопроводных систем и каналов передачи жидкостей и газов

2. В математике:

   • Исследование свойств цилиндров и различных методов расчета площади сечений
   • Разработка формул и алгоритмов для вычисления площади осевого сечения цилиндра

3. В физике:

   Определение объема и площади поверхности цилиндров для расчета объема и поверхности материалов и тел

Площадь осевого сечения цилиндра может изменяться в зависимости от размеров и формы сечения, а также от геометрических параметров самого цилиндра.

Понимание и рассмотрение площади осевого сечения цилиндра в различных контекстах позволяет улучшить процесс проектирования и анализа, а также способствует развитию математических и инженерных навыков.

Основные определения и свойства цилиндра

      Рассмотрим две   α   и   β   и произвольную   лежащую в плоскости   α   (рис. 1).

Рис.1

      Если из каждой точки окружности опустить   β,   то основания этих перпендикуляров образуют на плоскости   β   окружность радиуса   r,   центр   O₁   которой является основанием перпендикуляра, опущенного из точки   O   на плоскость   β   (рис.2).

Рис.2

      Определение 1.

	Отрезок , опущенного из любой точки окружности с центром   O   на плоскость  β ,   который заключен между плоскостями   α   и   β ,   называют образующей цилиндра.
	Совокупность всех образующих цилиндра называют цилиндрической поверхностью.
	Фигуру, ограниченную цилиндрической поверхностью и плоскостями   α   и   β,   называют цилиндром.
	Отрезок   OO1   называют осью цилиндра .
	на плоскости   α   с центром в точке   O   называют радиусом цилиндра.
	α   и   β ,   называют высотой цилиндра.
	Круги с центрами   O   и   O1   на плоскостях   α   и   β ,   называют основаниями цилиндра.

      Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра. Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра.

      Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

     Замечание 3. Прямая   OO₁   является цилиндра, а середина отрезка   OO₁   является цилиндра.

Виды цилиндров

1. Прямой цилиндр – имеет одинаковые симметричные основания (круг или эллипс), параллельные друг другу. Отрезок между точками симметрии оснований перпендикулярен им, является осью симметрии и высотой фигуры.
2. Наклонный цилиндр – имеет одинаковые симметричные и параллельные друг другу основания. Но отрезок между точками симметрии не перпендикулярен этим основаниям.
3. Косой (скошенный) цилиндр – основания фигуры не взаимно параллельны.
4. Круговой цилиндр – основаниями является круг. Также выделяют эллиптические, параболические и гиперболические цилиндры.
5. Равносторонний цилиндр – прямой круговой цилиндр, диаметр основания которого равен его высоте.

Сами прямые называют образующими цилиндрической поверхности.
Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.

Так как все образующие и ось перпендикулярны плоскости альфа, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).

Если построить ещё одну плоскость бета, которая будет параллельна плоскости альфа, то отрезки образующих, заключённые между плоскостями альфа и бета будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости бета, дают окружность, равную окружности, лежащей в плоскости альфа.

Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях альфа и бета) называется цилиндром.
Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.

Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.

Сечения цилиндра различными плоскостями

Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого – образующие, а две другие – отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).

Основные формулы

Формула для вычисления площади боковой поверхности цилиндра: Sбок=2пRL.

То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: Sполн=2пR(R+L).

Примеры и разбор решения заданий тренировочного модуля

Дан цилиндр.

Выберите значение площади его боковой поверхности

1. 60π
2. 192π
3. 120π
4. 36π

Решение:

Площадь боковой поверхности вычисляется по формуле: S=2πRL.

R=6, L=10

Подставим: S=2π·6·10=120π.

Ответ: 3) 120π

Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.

Решение:

Sполн=2πR(R+L)

По условию задачи L=R+6.

144π=2πR(R+R+6).

Получили квадратное уравнение относительно радиуса:

R2+6R-72=0

R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.

Ответ: 12.

Задача

Осевое сечение цилиндра – квадрат со стороной 20 см. Найти высоту цилиндра, радиус цилиндра, ось цилиндра и площадь основания цилиндра.

Решение

Одна из сторон осевого сечения – образующая (она же равна оси цилиндра и она же равна высоте). Значит, высота и ось равны 20 см. Далее, вторая сторона осевого сечения – диаметр основания. Он равен 20 см, значит, радиус – 10 см. Наконец, площадь основания ищется по формуле

Итак, ребята, на этом уроке мы изучили, что такое цилиндрическая поверхность, её образующая; цилиндр, все его элементы и сечения; площади поверхностей цилиндра.

Применение площади осевого сечения цилиндра

Площадь осевого сечения цилиндра — это величина, которая играет важную роль в различных областях науки и техники. Ее применение можно найти в следующих областях:

• Геометрия и математика: Площадь осевого сечения цилиндра используется для расчета объема и поверхностной площади цилиндрических тел. Она также позволяет определить высоту цилиндра по известным значениям радиуса и площади сечения.
• Строительство и инженерия: Площадь осевого сечения цилиндра используется при проектировании и расчете прочности конструкций, в которых применяются цилиндрические элементы, например, столбы, балки и трубы.
• Механика и физика: Площадь осевого сечения цилиндра важна при анализе момента инерции цилиндрического тела. Момент инерции позволяет определить сопротивление тела вращению и вычислить его кинетическую энергию.
• Металлургия и обработка материалов: Площадь осевого сечения цилиндра необходима для расчета объема материала, требуемого для изготовления цилиндрических деталей, например, валов, штанг и трубопроводов.
• Архитектура и дизайн: Площадь осевого сечения цилиндра может использоваться при проектировании колонн, столбов и других архитектурных элементов для создания эстетически приятных и функциональных конструкций.

В заключение, площадь осевого сечения цилиндра имеет широкое применение в различных областях науки и техники. Ее понимание и использование позволяют улучшить производительность, эффективность и надежность различных конструкций и процессов.

Площадь поверхности цилиндра

Площадь боковой поверхности

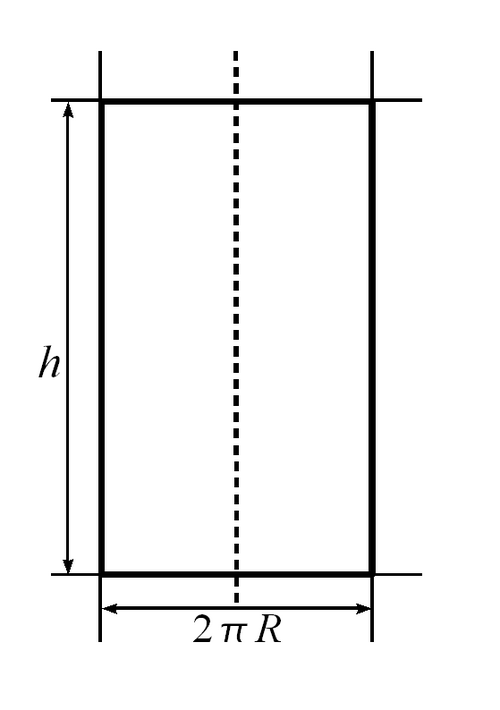
К вычислению площади боковой поверхности цилиндра

Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.

Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой и длиной , равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:

В частности, для прямого кругового цилиндра:

Для наклонного цилиндра площадь боковой поверхности равна длине образующей, умноженной на периметр сечения, перпендикулярного образующей:

Простой формулы, выражающей площадь боковой поверхности косого цилиндра через параметры основания и высоту, в отличие от объёма, к сожалению, не существует.

Площадь полной поверхности

Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.

Для прямого кругового цилиндра:

Отрывок, характеризующий Цилиндр

Цилиндр (круговой цилиндр) – тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра.

Основания цилиндра равны и лежат в параллельных плоскостях, а образующие цилиндра параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности. Боковую поверхность составляют образующие.

Цилиндр называется прямым, если его образующие перпендикулярны плоскостям основания. Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг одной из сторон как оси. Существуют и другие виды цилиндра – эллиптический, гиперболический, параболический. Призму так же рассматривают, как разновидность цилиндра.

На рисунке 2 изображён наклонный цилиндр. Круги с центрами О и О 1 являются его основаниями.

Радиус цилиндра – радиус его основания. Высота цилиндра – расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью цилиндра.

Плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

Призмой, вписанной в цилиндр, называется такая призма, основания которой – равные многоугольники, вписанные в основания цилиндра. Её боковые рёбра являются образующими цилиндра. Призма называется описанной около цилиндра, если её основания — равные многоугольники, описанные около оснований цилиндра. Плоскости её граней касаются боковой поверхности цилиндра.

Площадь боковой поверхности цилиндра можно вычислить, умножив длину образующей на периметр сечения цилиндра плоскостью, перпендикулярной образующей.

Площадь боковой поверхности прямого цилиндра можно найти по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой h и длиной P, которая равна периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:

В частности, для прямого кругового цилиндра:

P = 2πR, и S b = 2πRh.

Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.

Для прямого кругового цилиндра:

S p = 2πRh + 2πR 2 = 2πR(h + R)

Для нахождения объёма наклонного цилиндра существуют две формулы.

Можно найти объём, умножив длину образующей на площадь сечения цилиндра плоскостью, перпендикулярной образующей.

Объём наклонного цилиндра равен произведению площади основания на высоту (расстояние между плоскостями, в которых лежат основания):

V = Sh = S l sin α,

где l – длина образующей, а α – угол между образующей и плоскостью основания. Для прямого цилиндра h = l.

Формула для нахождения объёма кругового цилиндра выглядит следующим образом:

V = π R 2 h = π (d 2 / 4)h,

где d – диаметр основания.

blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Category:Cylinders
на Викискладе

Цили́ндр
(др.-греч. κύλινδρος

— валик, каток) — геометрическое тело , ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями, это основания цилиндра. Таким образом, граница основания будет по форме совпадать с направляющей.

В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность и основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.

Другие виды цилиндра — (по наклону образующей) косой или наклонный (если образующая касается основания не под прямым углом); (по форме основания) эллиптический, гиперболический, параболический.

Призма также является разновидностью цилиндра — с основанием в виде многоугольника.

Решение задач на тему «Цилиндр»

Пример 1 (Ященко 36 вариантов, 2021 год, вариант 10)

В цилиндрическом сосуде уровень жидкости достигает 25 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2,5 раза больше диаметра первого? Ответ дайте в см.

Решение: Раз переливают жидкость, значит это задача на объём.

Но при этом наши объёмы равны, жидкость то одна. 

Раз по условию диаметр второго сосуда в 2,5 раза больше, значит и радиус изменяется так же. Но тут нужно учесть «подвох» — радиус в формуле у нас возведён в квадрат. Вспоминая правило пропорции, считаем:

Ответ: 4

Пример 2 (Ященко 36 вариантов, 2021 год, вариант 26)

В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 6. Боковые рёбра призмы равны . Найдите объём цилиндра, описанного около этой призмы.

Решение: для нахождения объёма цилиндра, нам нужен радиус основания и высота. Но боковые рёбра призмы будут равны высоте цилиндра, раз по условию цилиндр описан около этой призмы. Значит, нужно посчитать только радиус основания.

В основании призмы прямоугольный треугольник. А мы знаем, что в таком случае, гипотенуза будет лежать на диаметре окружности. Значит, для нахождения радиуса нужно найти гипотенузу и поделить её на 2. 

Воспользуемся теоремой Пифагора. Наши катеты 5 и 6:

Значит, радиус будет равен:

Ну и находим объём цилиндра:

Ответ: 61

Пример 3

Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен R, его высота — Н, а расстояние между прямой АВ и осью цилиндра равно D. Найдите Н, если R=10, D=8, АВ=13.

Решение:

Связанные определения

Цилиндрическая поверхность
— поверхность, получаемая при движении прямой (образующей), параллельной какой-либо заданной, пересекающей кривую линию (направляющую), лежащую в не параллельной заданной прямой плоскости.
Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями называются основаниями цилиндра
.
Цилиндрическая поверхность между плоскостями оснований называется боковой поверхностью
цилиндра.
В случае параллельности плоскости основания и плоскости направляющей, граница основания будет по форме совпадать с направляющей.

Задача с прямым цилиндром

Покажем, как использовать полученные знания для решения следующей задачи. Пусть дан круглый прямой цилиндр. Известно, что осевое сечение цилиндра — квадрат. Чему равна площадь этого сечения, если всей фигуры составляет 100 см 2 ?

Для вычисления искомой площади необходимо найти либо радиус, либо диаметр основания цилиндра. Для этого воспользуемся формулой для общей площади S f фигуры:

Поскольку сечение осевое представляет собой квадрат, то это означает, что радиус r основания в два раза меньше высоты h. Учитывая это, можно переписать равенство выше в виде:

Теперь можно выразить радиус r, имеем:

Поскольку сторона квадратного сечения равна диаметру основания фигуры, то для вычисления его площади S будет справедлива следующая формула:

Мы видим, что искомая площадь однозначно определяется площадью поверхности цилиндра. Подставляя данные в равенство, приходим к ответу: S = 21,23 см 2 .

Стереометрия − это раздел геометрии, в котором изучаются фигуры в пространстве. Основными фигурами в пространстве являются точка, прямая и плоскость. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих существенных отличий стереометрии от планиметрии, так как во многих случаях задачи по стереометрии решаются путем рассмотрения различных плоскостей, в которых выполняются планиметрические законы.

В окружающей нас природе существует множество объектов, являющихся физическими моделями указанной фигуры. Например, многие детали машин имеют форму цилиндра или представляют собой некоторое их сочетание, а величественные колонны храмов и соборов, выполненные в форме цилиндров, подчеркивают их гармонию и красоту.

Греч. − кюлиндрос. Античный термин. В обиходе − свиток папируса, валик, каток (глагол − крутить, катать).

У Евклида цилиндр получается вращением прямоугольника. У Кавальери − движением образующей (при произвольной направляющей − «цилиндрика»).

Цель данного реферата рассмотреть геометрическое тело – цилиндр.

Для достижения данной цели необходимо рассмотреть следующие задачи:

− дать определения цилиндра;

− рассмотреть элементы цилиндра;

− изучить свойства цилиндра;

− рассмотреть виды сечения цилиндра;

− вывести формулу площади цилиндра;

− вывести формулу объема цилиндра;

− решить задачи с использованием цилиндра.

Площадь поверхности цилиндра

На рисунке видно, что цилиндр разрезали по образующей AB и развернули, получив при этом прямоугольник (боковую поверхность цилиндра) и два основания (окружности). Не трудно догадаться, что длина любой окружности будет равна длине стороны получившегося прямоугольника. Поэтому площадь боковой поверхности цилиндра можно найти с помощью площади прямоугольника. Просто одна из сторон найдётся как длина окружности, а вторая будет высотой цилиндра.

Формула обычно используется с радиусом, но можно и с диаметром. Кому как удобно.

Для нахождения площади полной поверхности цилиндра необходимо добавить 2 площади основания. А раз в основании окружность, то это будет две площади окружности.

Находим недостающие проекции точек на комплексных чертежах цилиндра и конуса

Ассоциативные чертежи в «Инженерной графике» называют комплексными.

Как найти недостающие проекции точек на комплексном чертеже цилиндра?

находим недостающие проекции точки m цилиндре

Построение недостающих проекций точек на цилиндре аналогично нахождению их на призме. Принцип тот же, только вместо граней, здесь окружность.  Для нашего цилиндра недостающие проекции точек К и М находятся, как показано на рисунке при помощи вертикальных и горизонтальных линий связи.

Подробнее о процессе построения смотрите на уроке как найти проекции точек на пирамиде и призме

Как найти недостающие проекции точек на комплексном чертеже конуса?

находим проекции точек на конусе

Необходимо построить недостающие проекции точек К и М на комплексном чертеже конуса.

Точка М задана фронтальной проекцией m’, точка К – горизонтальной проекцией k.

построения при нахождении горизонтальной проекции точки

Построим горизонтальную проекцию m. Для этого:

1. через точку m’ и вершину конуса s проводим вспомогательную прямую до пересечения ее с основанием в точке a.
2. Затем через полученную точку а проводим вертикальную  линию связи до пересечения с окружностью основания конуса в точке b.
3. Через полученную точку b и вершину конуса s проводим прямую.
4. Опускаем вертикальную линию связи из точки m’ до пересечения с прямой bs.
5. Горизонтальная проекция m найдена.

Профильная проекция m’’ находится обычным образом по линиям связи.

Фронтальная проекция (k’) находится таким же, вышеописанным образом. Вот рисунок

строим фронтальную проекцию точки k

Профильную проекцию (k’’) находим по линиям связи.

Окончательно комплексные чертежи цилиндра и конуса выглядят так.

готовый комплексный чертеж конуса

готовый комплексный чертеж цилиндра

Для лучшего понимания материала рекомендую посмотреть видеоурок.

Как найти высоту цилиндра

Рассмотрим варианты нахождения высоты фигуры, а также длины ее образующей (которая равна этой высоте).

Первым делом взглянем на формулу: \(V=\pi R^2\times H\), где V — объем цилиндра, R — радиус основания, H — высота фигуры.

Через эту формулу можем выразить высоту:

\(H=\frac V{\pi R^2}\)

Таким образом мы можем узнать H данного геометрического тела, если нам известен его объем и радиус. Если же вместо радиуса мы знаем диаметр, формула расчета будет выглядеть так:

\(H=\frac{4V}{D^2}\)

В случае, когда нам известен диаметр и площадь фигуры, мы так же можем найти высоту

Следует обратить внимание, что в зависимости от того, будет ли известна площадь боковой или полной поверхности, формула будет меняться

Для расчета S боковой поверхности (часть, ограниченная цилиндрической поверхностью) цилиндра мы используем формулу:

\(S=2\pi RH\)

выражаем H и получаем:

\(H=\frac S{2\pi R}\)

Если известна S полной поверхности (включает в себя площадь оснований фигуры), используем формулу:

\(S=2\pi R(H+R)=2\pi R\times H+2\pi R^2\)

выражаем H и получаем:

\(H=\frac{S-2\pi R^2}{2\pi R}\)

Для третьего способа нужно будет провести прямоугольное сечение, ширина которого должна будет совпадать с диаметрами оснований, а длина — с образующими цилиндра.

Таким образом, получается прямоугольный треугольник САВ. А так как высота равна образующей, мы можем вычислить ее по теореме Пифагора:

\(СВ^2=АС^2-АВ^2\)

\(H=СВ=\sqrt{АС^2-АВ^2}\)

Примечания

Wikimedia Foundation
.
2010
.

Синонимы

Смотреть что такое «Цилиндр» в других словарях:

— (лат. cylindrus) 1) геометрическое тело, ограниченное с концов двумя кругами, с боков плоскостью, огибающею эти круги. 2) в часовом мастерстве: особого рода рычаг двойного колеса. 3) шляпа, имеющая форму цилиндра. Словарь иностранных слов,… … Словарь иностранных слов русского языка

цилиндр
— а, м. cylindre m., нем. Zylinder <, лат. cylindrus <гр. 1. Геометрическое тело, образуемое вращение прямоугольника вокруг одной из его сторон. Объем цилиндра. БАС 1. Толстота цилиндра равна площади его основанья, помноженной на высоту. Даль … Исторический словарь галлицизмов русского языка

Муж., греч. прямая стопка, вал; облец, обляк; тело, ограниченное с концов двумя кругами, а с боков гнутою по кругам плоскостью. Толстота цилиндра равна площади его основанья, помноженной на высоту, геом. Паровой цилиндр, халява, труба, в которой… … Толковый словарь Даля

— высокая мужская шляпа из шелкового плюша с небольшими твердыми полями … Большой Энциклопедический словарь

ЦИЛИНДР, твердое тело или поверхность, образуемые вращением прямоугольника вокруг одной из его сторон в качестве оси. Объем цилиндра, если обозначить его высоту как h, а радиус основания как r, равен pr2h, а площадь изогнутой поверхности 2prh … Научно-технический энциклопедический словарь

ЦИЛИНДР, цилиндра, муж. (от греч. kylindros). 1. Геометрическое тело, образуемое вращением прямоугольника около одной из его сторон, называемой осью, и имеющее в основаниях круг (мат.). 2. Часть машин (двигателей, насосов, компрессоров и т.д.) в… … Толковый словарь Ушакова

ЦИЛИНДР, а, муж. 1. Геометрическое тело, образованное вращением прямоугольника вокруг одной из его сторон. 2. Колонновидный предмет, напр. часть поршневой машины. 3. Высокая твёрдая шляпа такой формы с небольшими полями. Чёрный ц. | прил.… … Толковый словарь Ожегова

— (Steam cylinder) одна из основных деталей поршневых машин. Выполняется в виде полого круглого Ц., в котором движется поршень. Ц. паровых машин снабжается обычно паровой рубашкой для обогревания его стенок в целях уменьшения конденсации пара.… … Морской словарь

Цилиндр

Опр.

Цилиндром называется тело, которое состоит из двух кругов, совмещаемых

параллельным переносом и всех отрезков, соединяющих соответствующие точки

этих кругов.

Круги называют основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей этих кругов – образующими цилиндра (рис. 1)

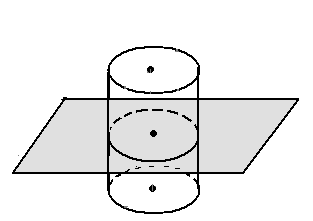
рис. 1 рис. 2 рис. 3 рис. 4

Свойства цилиндра:

1) Основания цилиндра равны и лежат в параллельных плоскостях.

2) Образующие цилиндра равны и параллельны.

Опр.

Радиусом цилиндра называется радиус его основания.

Опр.

Высотой цилиндра называется расстояние между плоскостями его оснований.

Опр.

Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.

Осевое сечение цилиндра – прямоугольник со сторонами 2R
и l

(в прямом цилиндре l

= Н) рис. 2

Сечение цилиндра, параллельные его оси, являются прямоугольниками (рис. 3).

Сечение цилиндра плоскостью, параллельной основаниям – круг, равный основаниям (рис. 4)

Площадь поверхности цилиндра.

Боковая поверхность цилиндра составлена из образующих.

Полная поверхность цилиндра состоит из оснований и боковой поверхности.

S

полн
= 2
S

осн
+
S

бок
;
S

осн
=
П
∙
R

2
;
S

бок
= 2
П
∙
R

∙Н
S

полн
= 2П
R

∙(R

+ Н)

Практическая часть:

№1.
Радиус цилиндра равен 3см, а его высота- 5см. Найдите площадь осевого сечения и площадь пол-

ной поверхности цилиндра.

№2.
Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 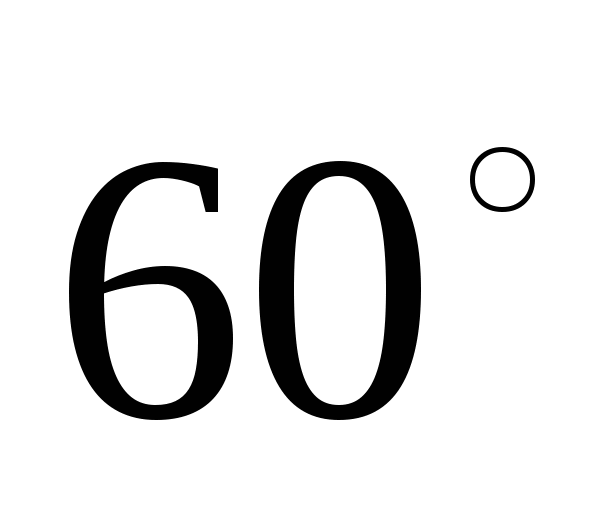и равна 20 см. Найдите площадь боковой поверхности цилиндра.

№3.
Радиус цилиндра равен 2см, а его высота- 3см. Найдите диагональ осевого сечения цилиндра.

№4.
Диагональ осевого сечения цилиндра, равная 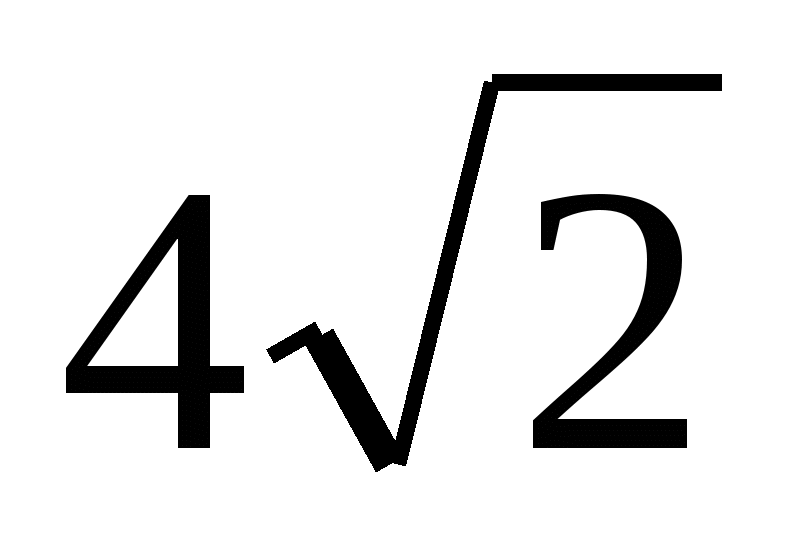, образует с плоскостью основания угол . Найдите площадь боковой поверхности цилиндра.

№5.
Площадь боковой поверхности цилиндра равна 15. Найдите площадь осевого сечения.

№6.
Найдите высоту цилиндра, если площадь его основания равна 1, а S
бок = .

№7.
Диагональ осевого сечения цилиндра имеет длину 8см и наклонена к плоскости основания под углом 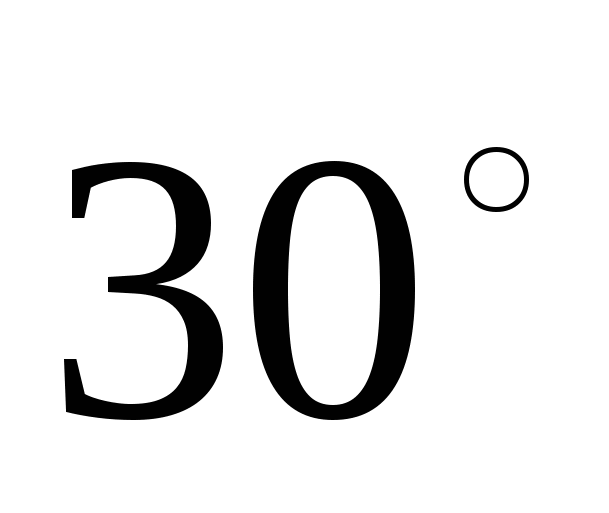. Найдите полную поверхность цилиндра.

Цилиндрическая дымовая труба с диаметром 65см имеет высоту 18м. Сколько жести нужно для её изготовления, если на заклепку уходит 10% материала?

Определение цилиндра как геометрической фигуры

Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».

Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны

Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.

«Компоненты» стереометрической фигуры

Цилиндр состоит из нескольких составляющих.

1. Цилиндрическая поверхность — это поверхность, которая образуется большим количеством параллельных прямых, проходящих через точки некоторой кривой.
2. Основания — это плоские фигуры, которые образованы пересечением ЦП с двумя параллельными плоскостями, ограничивающими цилиндр. Оснований у цилиндра два.
3. Боковой поверхностью называют часть ЦП, которая находится между основаниями.
4. И, наконец, высота — это отрезок, который высекается плоскостями оснований цилиндра на прямой, перпендикулярной им.

Примечание

Дополнительно можно измерить периметр S_бок. Для этого нужно длину окружности l сложить с высотой h и умножить данную сумму на 2.

Рассмотрим, как различаются типы рассматриваемой геометрической фигуры по форме. Цилиндр может быть:

1. Прямой. Его основания имеют центры симметрии, то есть являются кругами или эллипсами. При этом прямая между центрами перпендикулярна плоскостям оснований. Данная прямая называется осью цилиндра.
2. Косой. Его основания имеют центры симметрий, однако отрезок между ними не перпендикулярен плоскостям оснований.
3. Круговой. Имеет окружность в роли направляющей.
4. Прямой круговой. Его можно получить с помощью вращения прямоугольника вокруг одной из его сторон. Тогда эта сторона будет осью цилиндра и осью симметрии.
5. Равносторонний. Его диаметр равен высоте.
6. Эллиптический, гиперболический и параболический. Образованы соответственно эллипсами, гиперболами и параболами.
7. Усеченный. Геометрическое тело, которое отсекается от цилиндра плоскостью, не параллельной основанию.
8. Призма. Является разновидностью цилиндра, если имеет основание в виде многоугольника.

Основные формулы для вычисления боковой и полной площади

Кроме рабочих способов, перечисленных выше, рассчитать площадь рассматриваемого тела можно следующими методами:

1. Через диаметр и высоту: \( S_{полн.}=D\times\pi\left(h+\frac D2\right); S_{бок.}=D\times\pi\times h.\)
2. Через объем: \(S=\frac Vh.\)
3. Через длину окружности. Так как \(l=2\times\pi\times R\), то \(S_{бок.}=l\times h\), а \(S_{полн.}=l\times h+2\times\pi\times R^2\). 

Приведем примеры расчета.

Задача 1

Радиус ос­но­ва­ния цилиндра равен 2, высота равна 3. Высчитать площадь боковой поверхности цилиндра.

Решение

\(S_{бок.}=2\times\pi\times R\times h\)

Из этого: \(S_{бок.}=2\times3,14\times2\times3=6,28\times6=37,68.\)

Ответ: \(S_{бок.}=37,68.\)

Задача 2

\(S_{бок.}=24\pi\), а диаметр основания — 3. Узнать высоту цилиндра.

Решение

\(S_{бок.}=2\times\pi\times R\times h\)

Высоту отсюда вычислим так: 

\(h=\frac{S_{бок.}}{2\pi R}\)

Радиус равен: \(R=\frac D2. h=\frac{24\pi}{2\pi\times0,5D}=\frac{24\pi}{2\pi\times0,5\times3}=\frac{12}{1,5}=8\)