Академический рисунок куб поэтапно

Замкнутая и открытая композиция

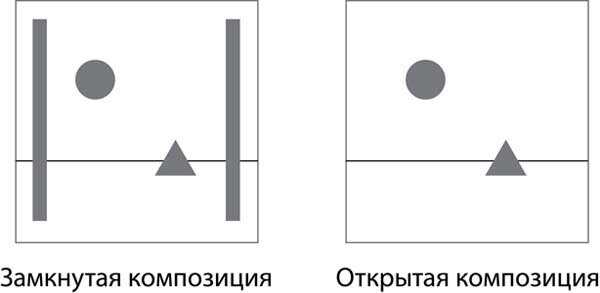
В замкнутой композиции основные направления линий стремятся к центру. Такая композиция подойдет для передачи чего-то устойчивого, неподвижного.

Элементы в ней не стремятся за рамки плоскости, а как бы замыкаются в центре композиции. А взгляд с любой точки композиции стремиться к этому центру. Для ее достижения можно использовать компактное расположение элементов в центре композиции, обрамление. Расположение элементов (на изображение — геометрических фигур) таким образом, чтобы все они указывали на центр композиции.

Открытая композиция, в которой направления линий исходят от центра, дает нам возможность продолжить мысленно картину и увести ее за рамки плоскости. Она подходит для передачи открытого пространства, движения.

Врезки шара и куба, когда секущие плоскости куба не проходят через центр шара

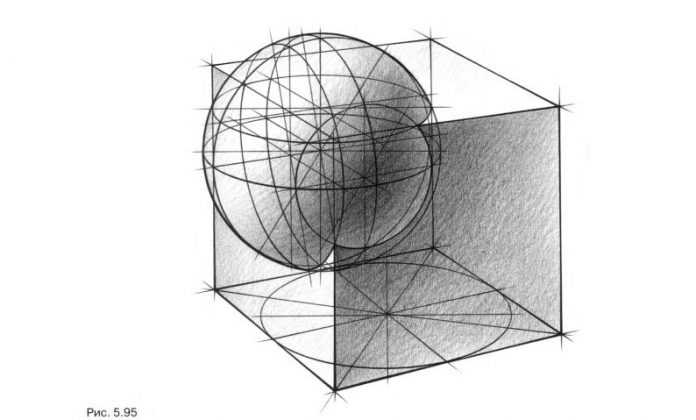
ЦЕЛЬ И ПОСТАНОВКА ЗАДАНИЯ. Чтобы научиться изображать врезки шара и куба, когда секущие плоскости куба не проходят через центр шара, сначала нарисуйте сложную врезку шара и куба в произвольном положении, а затем по заданным ортогональным проекциям.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ

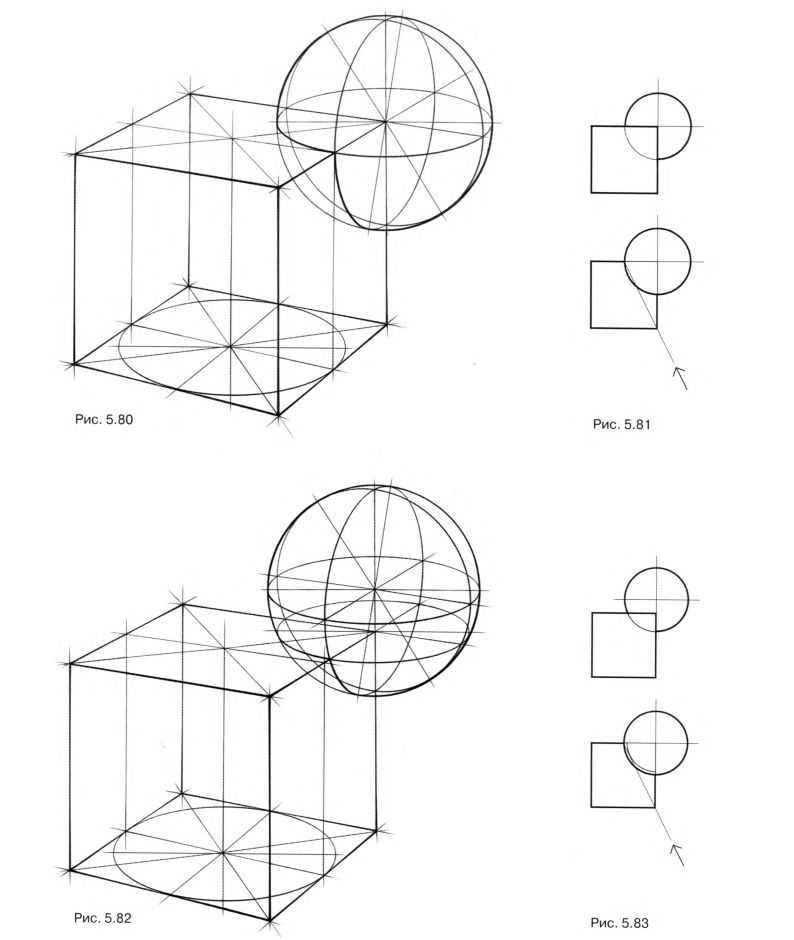
Рассмотрите рис. 5.80-5.87. Шар последовательно перемещается относительно куба, образуя связки различной сложности, причем каждая следующая связка имеет более сложную в построении линию врезки по сравнению с предыдущей. Для лучшего понимания перемещений шара и геометрии связок рядом с перспективными изображениями представлены ортогональные проекции.

На рис. 5.80 и 5.81 изображена самая простая связка, когда центр шара совпадает с вершиной куба. Построение линии врезки в этом случае сводится к построению трех центральных секущих плоскостей взаимно перпендикулярных направлений, соответствующих граням куба. Такое построение уже было разобрано нами ранее, теперь эта связка для нас – исходное положение для дальнейших построений.

На рис. 5.82 и 5.83 шар смещен вверх. При этом горизонтальная секущая шар плоскость – верхняя грань куба – переместилась вниз. Теперь для пересечения шара с горизонтальной гранью куба необходимо построить дополнительный горизонтальный эллипс, параллельный горизонтальному эллипсу, проходящему через центр шара. Раскрытие этого нового эллипса будет несколько больше раскрытия центрального горизонтального эллипса, так как он расположен дальше от линии горизонта. Полученная линия врезки (как и в исходном положении) замкнута и состоит из сегментов трех различных эллипсов. Точки, в которых один эллипс сменяет другой, лежат на ребрах куба.

На рис. 5.84 и 5.85 шар смещен влево относительно предыдущего положения. Линия врезки теперь пройдет по дополнительному вертикальному эллипсу, соответствующему по своему раскрытию центральному вертикальному эллипсу сечения.

На рис. 5.86 и 5.87 шар смещен назад от зрителя. При этом смещении появляется еще один дополнительный вертикальный эллипс.

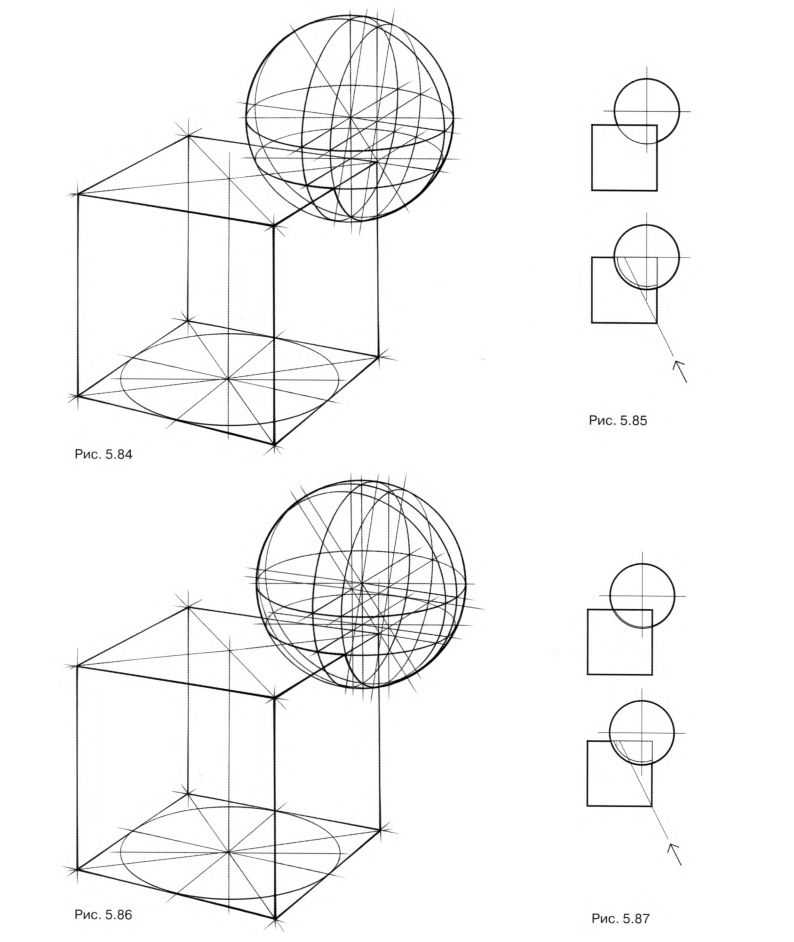
Для лучшего освоения материала изобразите рассмотренные связки куба и шара. Причем все четыре изображения могут быть соединены в одном рисунке. Только в этом случае перемещаться будет не шар, а куб. Сначала нарисуйте первую связку, когда центр шара совпадает с вершиной куба. Куб и секущие эллипсы изобразите легкими линиями. Затем на этом же рисунке опустите куб, нарисуйте новый куб и новую линию врезки. Продолжайте перемещать куб. С каждым новым перемещением на вашем рисунке будет появляться новый куб и новый секущий эллипс. Всякий раз незначительно усиливайте линии нового куба по сравнению с предыдущим. Последней связке придайте законченный характер: усильте основные линии и введите в рисунок легкий тон. При построении подобных сложных связок иногда можно и не изображать некоторые секущие эллипсы. Например, на связке, представленной на линейном рис. 5.88, в ортогональных проекциях на рис. 5.89 и в тональном рис. 5.90 сознательно не нарисован один из вертикальных эллипсов сечения, так как он не видим зрителю с данной точки.

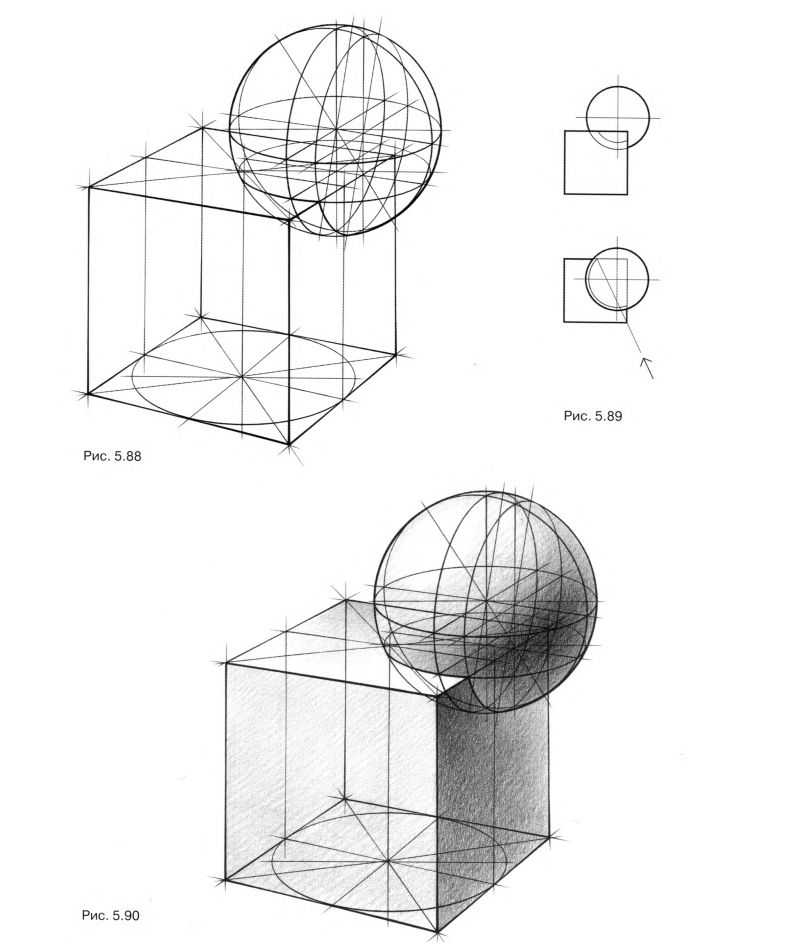
Теперь изобразите сложную связку куба и шара, заданную в ортогональных проекциях на рис. 5.91. Нарисуйте куб и найдите точку центра шара, для этого последовательно откладывайте координаты точки от ближайшей к центру шара вершины (рис. 5.92). Опишите окружность заданного диаметра вокруг центра шара.

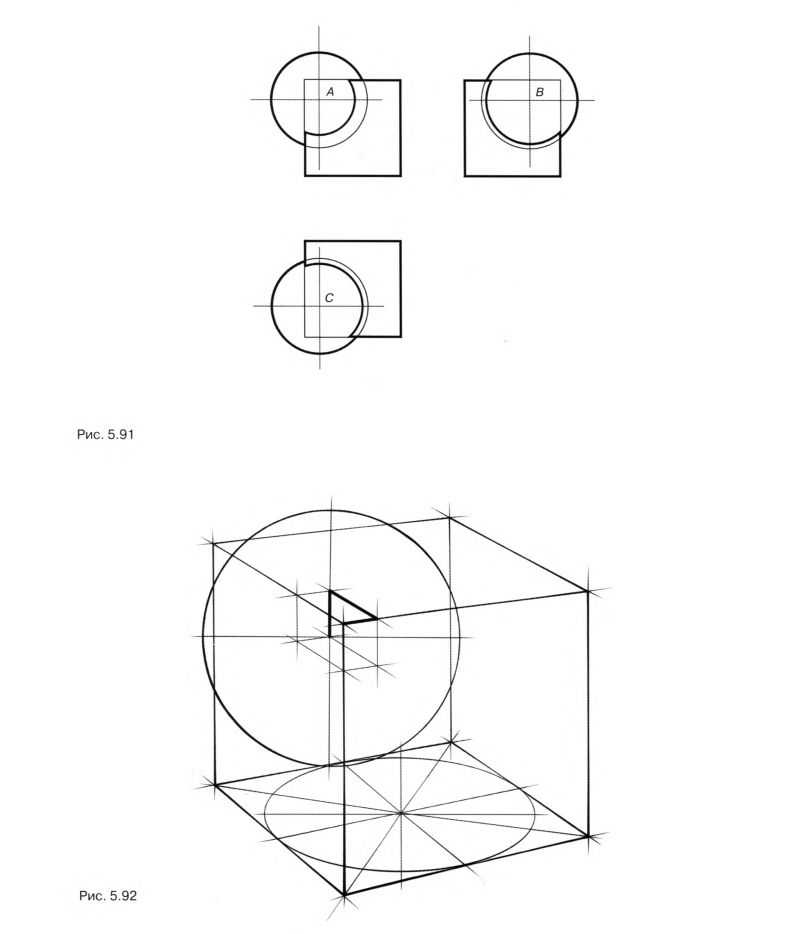
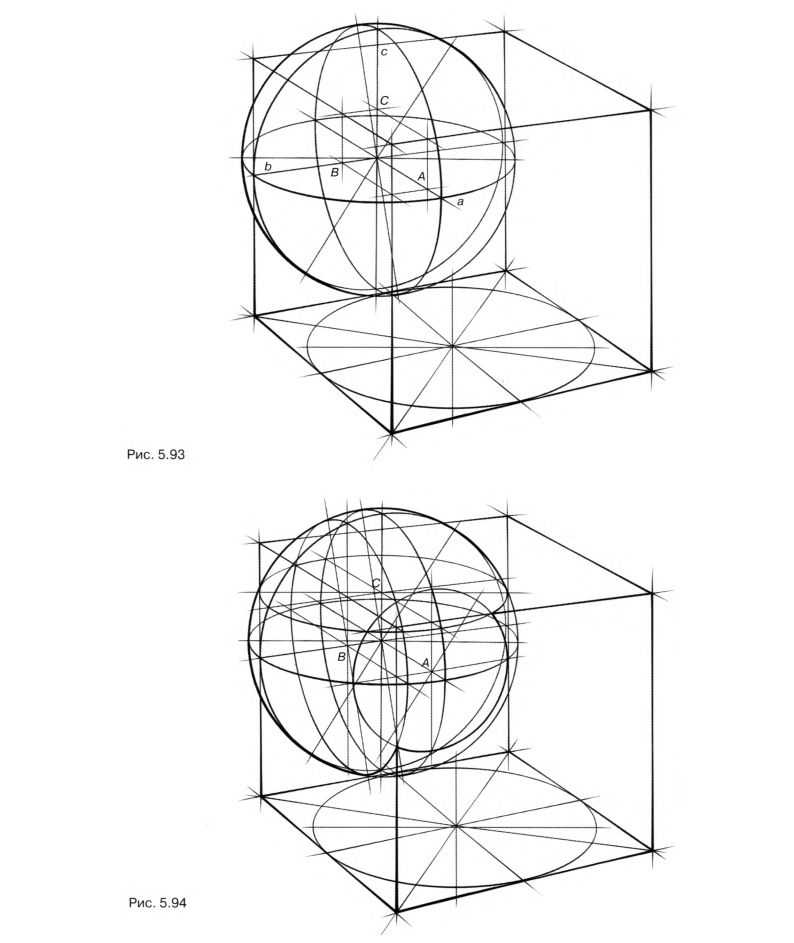
Постройте три взаимно перпендикулярных сечения шара, проходящих через его центр параллельно граням куба (рис. 5.93).

Изобразите линии пересечения шара и куба. Грани куба рассекают шар по трем окружностям. Чтобы изобразить эти окружности, необходимо сначала найти их центры. Обратитесь к ортогональным проекциям. Центры окружностей сечения – точки А, В и С – проекции центра шара на секущие плоскости (грани куба). Постройте проекции центра шара на секущие плоскости. Искомые точки лежат на пересечении граней куба с прямыми а, в и с, проходящими через центр шара параллельно его ребрам. Последовательно нарисуйте все три эллипса сечения, определяя оси каждого эллипса и точки, через которые он проходит. Проследите за тем, чтобы линия врезки была замкнута, а точки, в которых секущие эллипсы сменяют друг друга, лежали на ребрах куба (рис. 5.94).

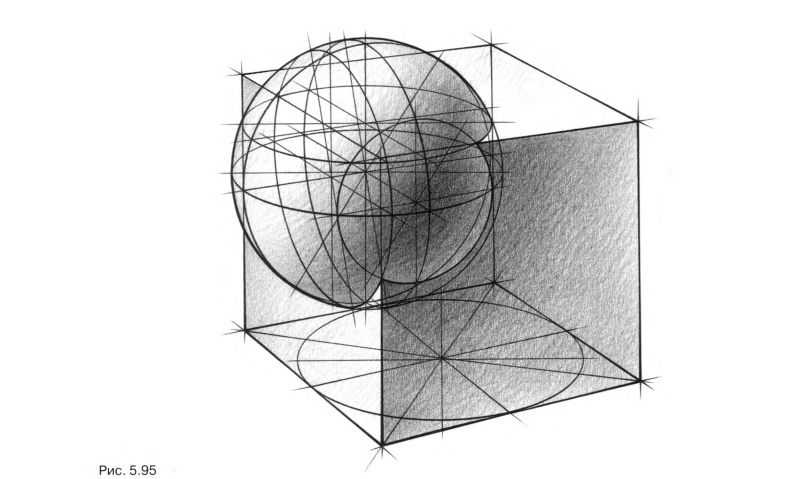
Теперь выполните упражнение на создание гармоничных связок куба и шара. Нарисуйте куб и шар в произвольном положении, например, как на рис. 5.96. Предложите несколько вариантов врезок, например, как на рис. 5.97; 5.98 и 5.99. Тонируйте любую связку (рис. 5.100). Для закрепления материала изобразите еще одну связку куба и шара (рис. 5.101) и тонируйте ее (рис. 5.102).

3D Blender уроки моделирования Как вырезать в кубе цилиндрическое отверстие

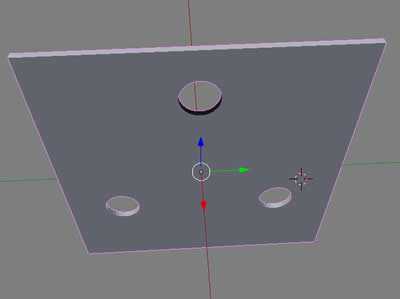
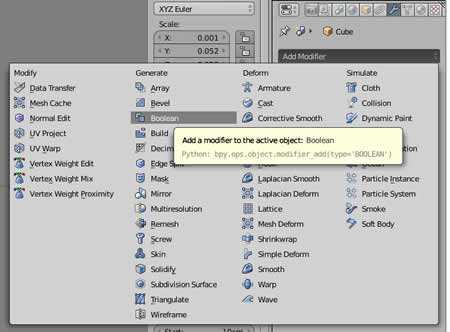
В Blender нажатие W в объектном режиме открывает доступ к так называемым булевым инструментам. Изменения объектов, производимые булевыми инструментами в компьютерной графике, основаны на логике булевых операций. Булевы операции, в свою очередь, — это подраздел математики; кроме того, булевы операции широко используются в программировании. Слово «булевы» заимствовано от фамилии Джоржа Буля, английского математика, труды которого лежат в основе математической логики.

Любая булева операция в компьютерной графике применяется к двум объектам. Ее результатом является третий объект, который представляет собой результат взаимодействия тем или иным способом двух исходный объектов.

В компьютерной графике (и Blender не исключение) широкое применение нашли следующие булевы способы взаимодействия объектов (соответственно им и называются булевы инструменты):

Intersect (пересекать). Результатом является объект, образованный пересечением двух исходных объектов. Другими словами, третий объект формируют наложенные области двух исходных.Union (объединение). Результатом является объект, образованный объединением двух исходных объектов.Difference (разность). Результатом является объект, образованный вычитанием второго из первого, т.е. от первого объекта отрезается часть, которую перекрыл второй объект. Что из чего будет вычитаться, зависит от того, какой объект был выделен первым.

Врезка куба и цилиндра

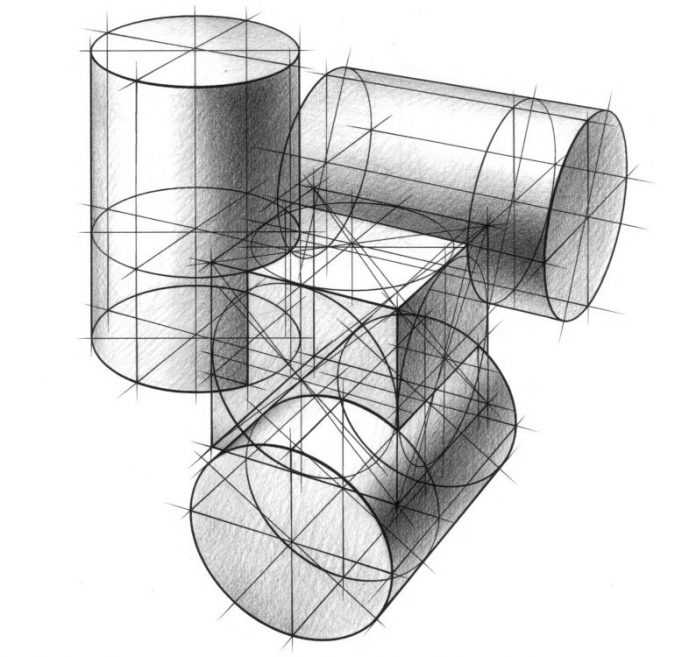
ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку куба и цилиндра. Оценить многообразие возможных свя­зок куба и цилиндра, отработать приемы построе­ния их врезок, научиться создавать на листе связки с гармоничными пропорциями.

ПОСТАНОВКА ЗАДАНИЯ. Нарисуйте связки куба и цилиндра сначала по заданным ортогональным проекциям, а затем в произвольном положении по отношению друг к другу. Найдите наиболее краси­вые, гармоничные пропорции связок, изменяя поло­жение линии пересечения геометрических тел.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

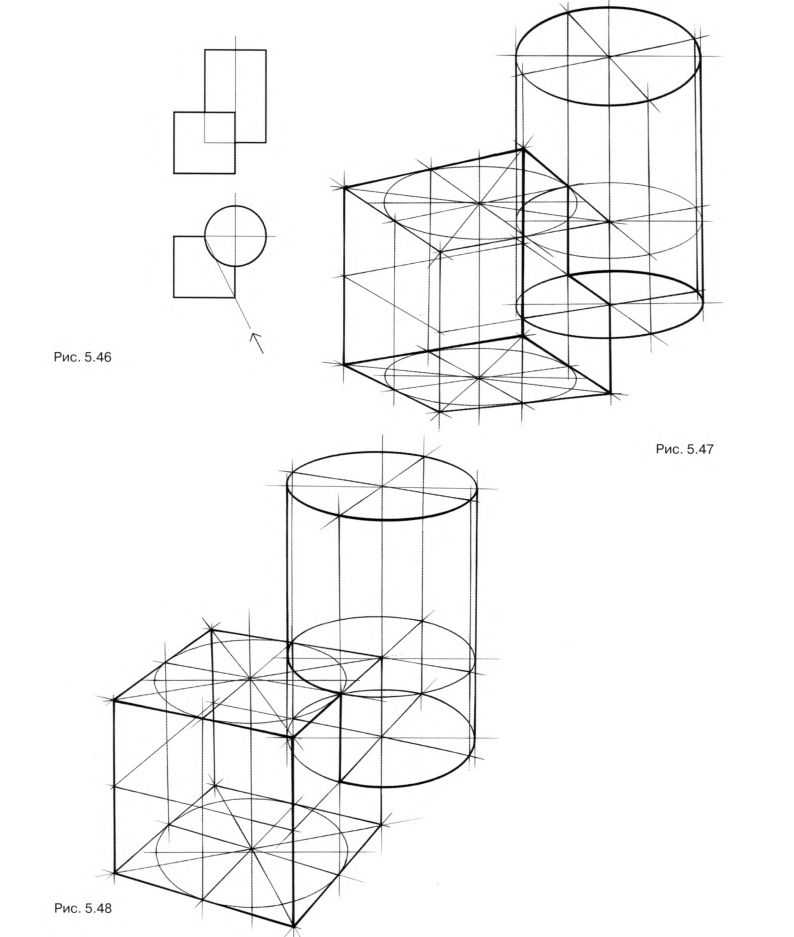
Рассмотрите ортогональные проекции двух геомет­рических тел — куба и цилиндра — на рис. 5.46. Пред­ставьте взаимное положение тел. Изобразите в пер­спективе заданную связку куба и цилиндра с раз­личным положением относительно линии горизонта (выше линии горизонта на рис. 5.47 и ниже линии горизонта на рис. 5.48).

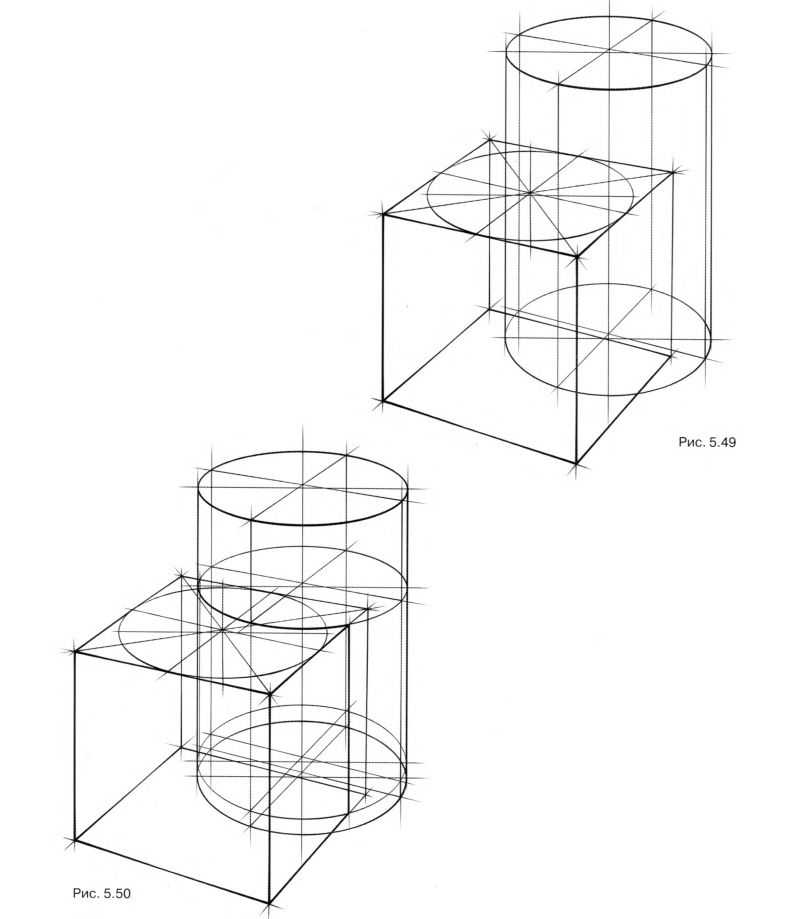
Изобразите куб и вертикальный цилиндр в поло­жении, представленном на рис. 5.49. Предложите несколько вариантов врезок, например, как на рис. 5.50 и 5.51. Тонируйте любую связку (рис. 5.52).

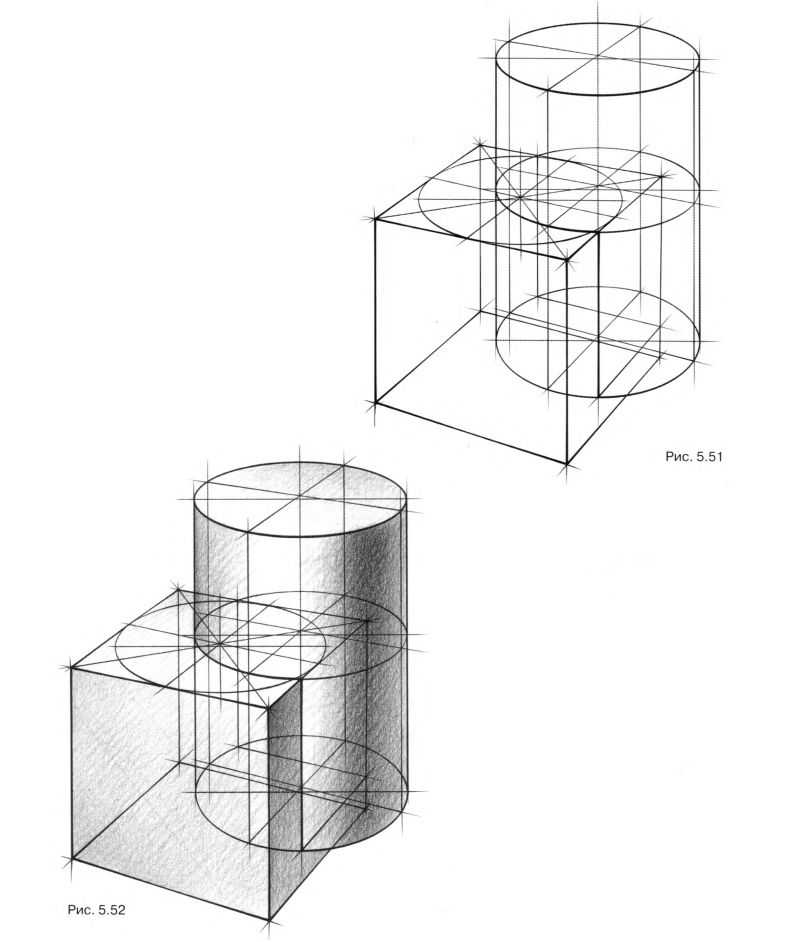
Изобразите куб и горизонтальный цилиндр (рис. 5.53). Предложите гармоничные врезки, например, как на рис. 5.54 и 5.55 (тон на рис. 5.56). Теперь попробуйте сделать подобное упражне­ние, увеличив количество геометрических тел. Связка тел — куба и трех цилиндров — предлагается на рис. 5.57. Постройте врезки, например, как это сделано на рис. 5.58. Легко тонируйте композицию (рис. 5.59).

Рисунок конуса

Конус представляет собой симметричное тело вращения, образующая конуса начинается в его вершине, совпадающей с осью вращения и заканчивается в основании. В нашем случае конус прямой, его ось перпендикулярна основанию.

При рисовании конуса сперва намечаем место и размер изображения в листе. Конус не должен быть слишком большим или маленьким, разместить его следует выше середины листа. Оптически верх конуса легче, вокруг него больше свободного пространства, поэтому конус в рисунке следует разместить выше, чем, это делается обычно.

Затем отмечаем засечкой самую верхнюю часть конуса и проводим горизонтальную ось основания. Определив таким образом высоту, определяем, насколько ширина основания меньше высоты. Рисуем засечки, ограничивающие ширину основания. При этом учитываем, что эллипс, после того, как он будет построен, немного увеличит высоту конуса.

Только после того, как определена высота и ширина, по центру проводим вертикальную ось симметрии.

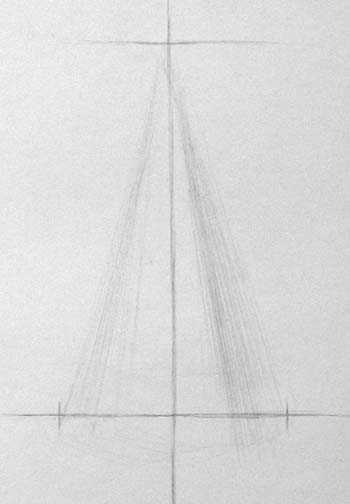
Соединяем вершину конуса с основанием. Линии с краю являются самыми удалёнными от рисовальщика поверхностями, поэтому их следует рисовать светлыми.

Следующий этап — построение эллипса

При построении эллипса важно точно определить его раскрытость, насколько малый диаметр (видимый вертикальный размер) меньше, чем его ширина. Чтобы передать объём в линии, ближнюю часть овала сделаем темнее

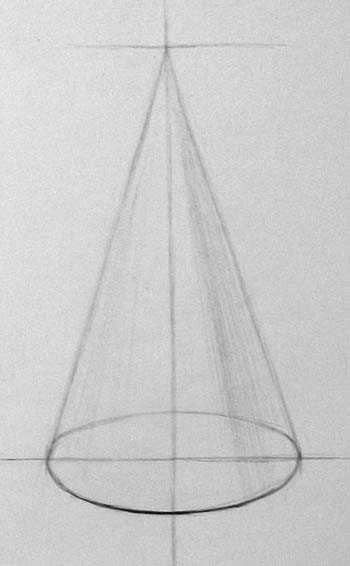
После того, как построение проверено, можно продолжить изображение объёмной формы конуса. Сперва находим границу света и тени. Граница представляет собой прямую линию, идущую от вершины к точке в основании. Постарайтесь верно определить, каково соотношение части, видимой на свету и части в тени. В верхней части линия немного чётче, в нижней части конуса она более плавно размыта к краям. Связано это с тем, что ближе к вершине конуса форма заворачивается сильнее, она почти приближается к угловой форме, какую мы видим на примере куба. Теневая поверхность удаляется от нас, дальний край по закону воздушной перспективы будет светлее.

Освещённая часть удаляется от зрителя, поэтому, в соответствии с законами воздушной перспективы, она будет темнее. На границе света и тени мы видим полутон, промежуточную поверхность между светом и тенью, он относится к свету, но темнее, чем освещённая часть предмета, т. к. угол падения лучей света здесь небольшой. Падающая тень темнее тени собственной. Она лежит на горизонтальной поверхности, передняя часть тени темнее. Штрих кладём по форме, сначала в направлении лучей, идущих от вершины к основанию.

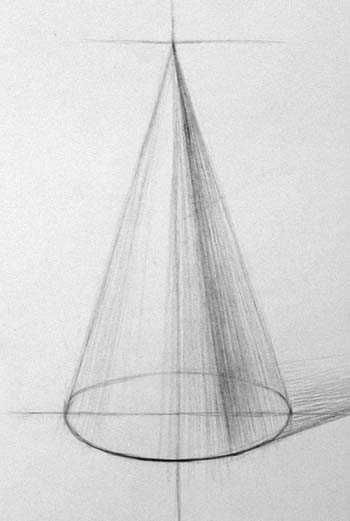
Для лучшей передачи формы введём горизонтальные линии штриховки, показывающие сечение формы по горизонтали

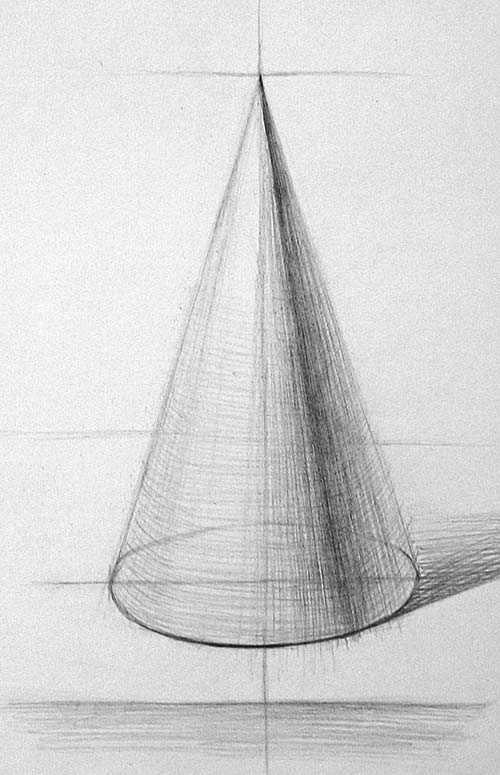
Особенно важно показать, как форма заворачивается по краям. На завершающем этапе работы уточняем тональные отношения и форму

Освещённая часть чуть темнее снизу, сверху выше контраст света и тени. Теневая часть конуса снизу подсвечена рефлексом от поверхности стола, также имеется рефлекс, проходящий по дальнему краю формы.

Примеры в живописи

Геометрические формы нашли свое место и в живописи, наряду с романтизмом и прочими направлениями. Ярким примером тому является художник Хуан Грис и его самая знаменитая картина «Мужчина в кафе», которая, словно мозаика, состоит из треугольников, квадратов и окружностей. Еще одна абстрактная композиция из геометрических фигур — холст «Пьеро», художника Б. Кубишта. Яркая, четкая и очень своеобразная картина.

Перспектива
композиции выполняется по индивидуальному
заданию. Номер индивидуального задания
соответствует порядковому номеру по
списку в журнале группы. Индивидуальные
задания в таблице №3

Таблица№

№Варианта		Параллелепипед	Пирамида	Конус	Цилиндр
		Т=10, =60, АВ=80, АЕ=40,
		T=20, =55,
			T=10, =60,
			T=10, =50,
		T=10, =50,
			T=20, =60,
			T=40, =50,
		T=20, =50,
		T=30, =50,
		T=10, =60,
		T=25, =55,
		T=15, =60,
			T=20, =50,
			T=10, =50,
			T=10, =55,
		T=10, =50,
			T=30, =55,
			T=15, =60,
		T=40, =50,

Указания к
выполнению ЛИСТА 1

Перед выполнением
перспективного изображения композиции
геометрических тел следует сначала
составить саму композицию, т. е. определить
взаимное расположение объектов, их
положение относительно главной линии
картины, расстояния от плоскости картины.
В зависимости от составленной композиции
можно выбирать положение точки зрения
(высоту точки зрения и дистанцию).
Дальность точки зрения выбирается
равной одному габариту композиции.
Высота точки зрения выбирается или
несколько меньшей или несколько большей
высоты самого высокого объекта.

В индивидуальном
задании определена форма объектов, их
размер, угол поворота к картинной
плоскости, расстояние от плоскости
картины. Требуется построить перспективу
композиции дух гранных тел, одно из
которых расположено фронтально по
отношению к картинной плоскости, другое
– с заданным углом поворота к картине
и одного тела вращения.

При выполнении
перспективного изображения композиции
геометрических тел имеет смысл провести
подготовительную работу – построить
план будущей композиции. Этот план можно
просто нарисовать или, вырезав из бумаги
контуры планов геометрических тел и
двигая их по плоскости, выбрать наилучшее
композиционное решение, а также определить
положение объектов на предметной
плоскости и расстоянии между ними. При
этом выяснится общий габаритный размер
композиции, что определит положение
высоты точки зрения, и дистанцию
(расстояние от наблюдателя до картины).

Пример ЛИСТА 1 —
перспективного изображения композиции
геометрических тел приведен на(рис.
91
)

Перспектива
интерьера

Интерьером
называется внутренний вид помещения в
целом или отдельных его частей. В практике
построения интерьеров известны различные
способы изображения интерьеров, в
зависимости от задачи, которую ставит
перед собой художник. В данном пособии
рассматривается один из способов
построения интерьера с помощью
перспективных масштабов. В зависимости
от расположения стен помещения
относительно картины изображение
интерьера может быть фронтальным или
угловым. Если одна из стен помещения
расположена параллельно картине, то
такое изображение называется фронтальной
перспективой интерьера. Если стены
помещения находятся под углом к картинной
плоскости, то такое изображение называется
угловой перспективой интерьера.

Композиция из геометрических фигур рисунок. Построение перспективы композиции геометрических тел

Основной задачей вступительных испытаний по композиции является проверка творческих способностей и навыков абитуриентов в области моделирования объемной архитектурной композиции , правил построения ее ортогональных проекций и выполнения соответствующей им перспективного рисунка со светотеневой проработкой, умения выполнять линейный эскизный рисунок.

При выполнении экзаменационной работы необходимо соблюдать следующие условия:

1. Каждый абитуриент получает экзаменационный билет с заданными в ортогональных проекциях (фронтальный вид и вид сверху) связкой из трех геометрических тел, линией горизонта и точки в пространстве, откуда он наблюдает будущую композицию. В билете также задана тема композиции (Н-р: вертикальное развитие, горизонтальное развитие). Пропорции заданных элементов при составлении композиции не меняются

2. Добавляя к заданной связке из трех элементов другие геометрические тела, необходимо составить целостную объемную композицию и выполнить ее ортогональные проекции (план, фасад) и перспективный рисунок. Геометрические тела, добавляемые в композицию, выбираются абитуриентом самостоятельно из элементов (заданных типов, представленных в приложении к билету), которые могут иметь измененные размеры и пропорции.

3. Используемые геометрические тела:– куб;– параллелепипед с квадратным основанием;– цилиндр;– пирамида;– конус;– трехгранная призмы;– квадратная, прямоугольная, круглая, трехгранная пластины.

В композиции должны быть использованы не менее 5 типов элементов.

4. Общее количество элементов в композиции 12-15

5. Все элементы композиции должны быть расположены в параллельно-перпендикулярных плоскостях. Связь элементов между собой осуществляется через врезки или наложением плоскостей. Не допускается соединение в одной плоскости граней соседних форм и совмещения их ребер.

6. В перспективном рисунке композиции обязательно использование двух точек схода, размещенных за пределами листа. Линия горизонта может иметь верхнее (“птичка”) или нижнее положение (соответствующее горизонту восприятия идущего человека по отношению к объемной модели), которое задается экзаменационным билетом. Линии построения и невидимые контуры форм сохраняются.

7. Композиция изображается на плоскости.

8. Обязательно использовать в композиции тела вращения.

9. Использование в работе угольника и линейки не допускается.

10. Каждый абитуриент должен выполнить вариант эскиза к работе в линейной графике.11. Для светотеневой проработки композиции, направление освещения абитуриент выбирает произвольно. При этом падающие тени от предмета на предмет в композиции не показываются.

Экзаменационное задание выполняется на формате А2 (40х60см) в течение 4 часов (240мин.)

Эскизы выполняются на отдельном листе формата А3

После выполнения работы в экзаменационную комиссию сдаются:

– Выданный билет– Лист с 2 эскизами, выполненными в линейной графике (формат А 3)– Лист с объемной архитектурной композицией и 2 ортогональными проекциями (формат А 2)

http://risunokgfn.ru/5.htmhttp://gallerix.ru/learn/konstruktivnyj-risunok-natyurmorta-iz-geometricheskix-tel/4/http://vk.com/topic-129840611_39606815

голоса

Рейтинг статьи

ТРЕУГОЛЬНИК В КОМПОЗИЦИИ

Треугольник — наиболее часто встречающаяся в природе форма. Треугольник — самая динамичная, неустойчивая форма, которая ассоциируется с движением, развитием, скоростью. В положении «вершиной вверх» вызывает образы устойчивости, стабильности (пирамида). Несколько треугольников — позитивное динамическое движение. В положении «вершиной вниз» — шаткое равновесие, балансировка. В отличие от прямоугольника, стороны не противостоят друг другу, а меняют направление развития. Это может быть использовано для создания конкретных образов. Треугольник естественным образом вносит в композицию ощущение глубины пространства.

Правило золотого сечения

Различное расположение элементов на плоскости может создать гармоничное или негармоничное изображение. Гармония — это ощущение и понятие о правильном расположении элементов весьма интуитивно. Однако можно выделить несколько совсем не интуитивных правил.

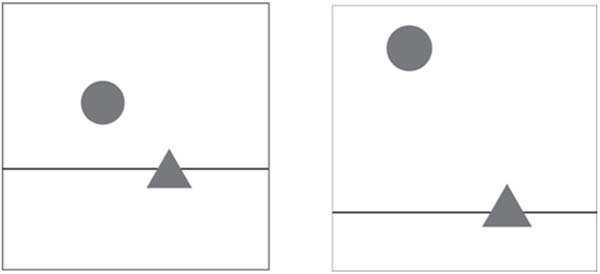
Расположение простых геометрических фигур на изображении слева выглядит намного более гармоничным. Почему?

Гармония
— это слаженность. Единое целое, в котором все элементы дополняет друг друга. Некий единый механизм.

Самый большой такой механизм — это окружающий нас мир, в котором все элементы взаимосвязаны — животные дышат воздухом, расходуют кислород, выдыхают углекислый газ, растения используют его углерод и энергию солнца для фотосинтеза, возвращая кислород. Одни животные питаются этими растениями, другие регулируют количество питающихся растениями, питаясь ими, тем самым спасая растения, вода испаряется, чтобы выпасть осадками и пополнить запасы рек, океанов и так далее…

Нет ничего более гармоничного, чем сама природа. Поэтому и понимание гармонии приходит к нам от нее. А в природе огромное количество зрительных образов подчиняется двум правилам: симметрии
и правилу золотого сечения
.

Что такое симметрия, я думаю, вы знаете. А что такое золотое сечение?

Золотое сечение
можно получить, если разделить отрезок на две неравные части таким образом, чтобы отношение всего отрезка к большей части равнялось отношению большей части отрезка к меньшей. Это выглядит так:

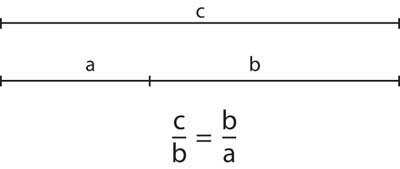
Части этого отрезка примерно равны 5/8 и 3/8 от всего отрезка. То есть, по правилу золотого сечения зрительные центры в изображении будут располагаться так:

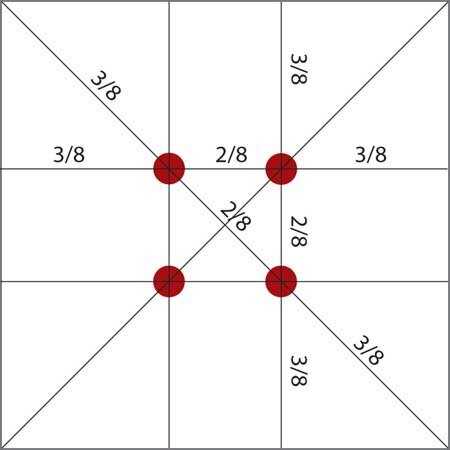
Рисунок «врезки»

«Врезкой» сокращенно называют задание по учебному перспективному рисунку, которое часто предлагают на вступительных экзаменах в художественные и архитектурные вузы.

«Врезка» — это абстрактная композиция из объемных геометрических тел, которые пересекаются между собой в пространстве, частично как бы вставлены, «врезаны» друг в друга. Геометрических фигур в такой композиции может быть довольно много, в среднем 5-10. Группа тел должна представлять некую цельную, достаточно эстетичную конструкцию, быть гармоничной, выразительной, и должна быть грамотно расположена в пространстве листа. Как правило, в задании предусмотрен формат А2.

Композицию нужно изобразить строго по правилам перспективы, с учетом точки зрения и положения линии горизонта.

Для компоновки врезки предлагается использовать основные, простейшие геометрические фигуры: куб, параллелепипед, шар, цилиндр, конус, призму, пирамиду. Фигуры можно делить на части, делать в них вырезы, но они должны оставаться узнаваемыми.

Предварительно, конечно, вы должны получить опыт рисования с натуры гипсовых геометрических тел.

Как правило, не рекомендуется ориентировать фигуры в пространстве под наклонными углами.

Самое сложное в этом задании — необходимость представить и правильно изобразить видимые и даже невидимые линии пересечения изображаемых объемных тел.

Мой совет — не стоит активно использовать такие взаимные пересечения тел, которые трудно себе представить мысленно, сложные по построению даже в виде чертежа. Не только прорисовать их пересечение сложно, но и оценить качество выполнения работы будет трудновато. Это, например, некоторые варианты взаимного пересечение цилиндра и шара, вообще тел вращения между собой. Более выразительны и понятны пересечения криволинейных поверхностей и плоскостей.

Пересечение шара и плоскости — всегда окружность, поэтому линия пересечения фигур пойдёт по эллипсу.