Как найти объём тела вращения с помощью интеграла

Решение примеров

Интегрирование по частям:

1. $\int\text{arctg}\:xdx$Решение

   $\int\text{arctg}\:xdx=\begin{bmatrix}\text{arctg}\:{x}=u, du=\displaystyle\frac{dx}{1+x^2}\\dx=dv, v=x\end{bmatrix}=x\:\text{arctg}\: {x}-\int\displaystyle\frac{xdx}{1+x^2}=\\=x\:\text{arctg}\: {x}-\displaystyle\frac{1}{2}\int\displaystyle\frac{dx^2}{1+x^2}=x\:\text{arctg}\: {x}-\displaystyle\frac{1}{2}\ln(1 + x^2) + C.$

2. $\int x\sin{x}dx$Решение

   $\int x\sin{x}dx=\begin{bmatrix}x=u, du=dx\\ \sin{x}=dv, v=-\cos{x}\end{bmatrix}=-x\cos{x}+\int\cos{x}dx=\\=-x\cos{x}+\sin{x}+C.$

3. $\int xe^{x}dx$Решение

   $\int xe^{x}dx=\begin{bmatrix}u=x, du=dx\\dv=e^{x}dx, v=e^x\end{bmatrix}=xe^x-\int e^{x}dx=xe^x-e^x+C.$

Замена переменной:

Применение определенного интеграла при решении физических задач.

Определенный интеграл широко применяется при решении различных физических задач. С помощью определенного интеграла можно вычислять: путь, пройденный материальной точкой, если известна скорость движения; ; силу давления жидкости на плоскую фигуру; статические моменты и координаты центра масс плоской кривой и плоской фигуры и так далее.

Пусть плоская пластинка \(G\), имеющая форму криволинейной трапеции, определяемой условиями \eqref{ref1}, погружена вертикально в жидкость с плотностью \(\rho\) так, что ее боковые стороны параллельны поверхности жидкости и удалены от уровня жидкости на расстояния \(a\) и \(b\) (рис. 37.10). Требуется найти силу давления жидкости на пластинку.

Рис. 37.10

Из курса физики известно, что если пластинка погружена в жидкость и расположена горизонтально на расстоянии \(h\) от поверхности жидкости, то сила давления \(\mathcal{P}\) на одну из сторон пластинки равна
$$
\mathcal{P} = g \rho hS,\nonumber
$$
где \(S\) — площадь пластинки, \(g\) — ускорение силы тяжести. Таким образом, сила давления — линейная функция от глубины погружения пластинки. Поэтому естественно разбить пластинку \(G\) на части прямыми, параллельными поверхности жидкости (оси \(Oy\)).

Пусть \(T = \{x_{i},\ i = \overline{0, n}\}\) — разбиение отрезка \(\). Прямыми, проведенными через точки \(x_{i}\ (i = \overline{1, n-1})\), разобьем фигуру \(G\) на \(n\) частей (полосок) \(G_{i}\ (i = \overline{1, n})\). Выделим полоску \(G_{i}\), ограниченную прямыми \(x = x_{i-1}\) и \(x = x_{i}\) (рис. 37.10). Площадь этой полоски приближенно равна площади прямоугольника с основанием \(\Delta x_{i}\) и высотой \(f(x_{i})\), глубину погружения всех точек полоски \(G_{i}\) можно считать равной \(x_{i}\). Поэтому сила давления жидкости на полоску \(G_{i}\) приближенно равна
$$
g \rho x_{i}f(x_{i})\Delta x_{i},\nonumber
$$
а сумма
$$
\mathcal{P}_{T} = \sum_{\substack{i=1}}^{\substack{n}} g \rho x_{i}f(x_{i})\Delta x_{i}\nonumber
$$
приближенно равна силе давления жидкости на пластинку \(G\).

Если \(l(T) \rightarrow 0\), где \(l(T)\) — мелкость разбиения \(T\), а функция \(f\) непрерывна на отрезке \(\), то    \(\mathcal{P}_{T} \rightarrow \mathcal{P}\), где
$$
\mathcal{P} = g \int\limits_a^b \rho x f(x)\ dx.\label{ref41}
$$
Число \(\mathcal{P}\) выражаемое формулой \eqref{ref41}, называют силой давления жидкости на пластинку \(G\).

Пример 8.

Вычислить силу давления \(\mathcal{P}\) жидкости с плотностью \(\rho\) на вертикальную стенку, имеющую форму полукруга радиуса \(R\) и погруженную в жидкость так, что диаметр полукруга расположен на поверхности жидкости (рис. 37.11).

Рис. 37.11

(\triangle\) Выберем систему координат так, как указано на рис. 37.11. Пользуясь формулой \eqref{ref41}, где \(f(x) = \sqrt{R^{2}-x^{2}},\ a = 0,\ b = R\), получаем
$$
\mathcal{P} = 2g \rho \int\limits_0^R x \sqrt{R^{2}-x^{2}}\ dx =-\left.\frac{2}{3} g \rho (R^{2}-x^{2})^{3/2}\right|_{0}^{R} = \frac{2\rho g}{3} R^{3}.\ \blacktriangle\nonumber
$$

Вычисление объема тел с помощью интеграла

Понятие интеграла является довольно обширным и делится на несколько классов: определенный/неопределенный, двойной/тройной/одиночный.

Известно, что определенный интеграл численно равен площади под кривой, уравнение которой находится под интегралом.

Перейдем от задач на плоскости к задачам в пространстве. Пусть дано цилиндрическое тело D. Зададим оси координат так, что бы основание D — σ лежало в плоскости XOY, а поверхность, задаваемая функцией f(x, y) ограничивала тело D сверху.

Тогда объем тела D можно вычислить по формуле: 

Далее рассмотрим случаи нахождения объемов с помощью двойных и тройных интегралов. Советуем составить краткие конспекты алгоритмов расчета.

Вычисление длины дуги кривой.

Утверждение 6.

Если кривая \(\Gamma\), заданная уравнением
$$
\Gamma = \{\boldsymbol{r} = \boldsymbol{r}(t),\ \alpha \leq t \leq \beta\},\label{ref22}
$$
непрерывно дифференцируема, то ее длина \(S\) выражается формулой
$$
S = \int\limits_{\alpha}^{\beta} |\boldsymbol{r}'(t)|\ dt.\label{ref23}
$$

\(\circ\) было доказано, что непрерывно дифференцируемая кривая \(\Gamma\) спрямляема (имеет длину), а производная переменной длины дуги \(s(t)\) этой кривой выражается формулой
$$
s'(t)\ dt = |\boldsymbol{r}'(t)|.\label{ref24}
$$
Пусть \(S\) — длина всей кривой \(\Gamma\); тогда, используя равенство \eqref{ref24} и , получаем
$$
\int\limits_{\alpha}^{\beta} |\boldsymbol{r}'(t)|\ dt = \int\limits_{\alpha}^{\beta} s'(t)\ dt = s(\beta)-s(\alpha) = S.\nonumber
$$
так как \(s(\beta) = S\), a \(s(\alpha) = 0\). \(\bullet\)

Если \(\boldsymbol{r}(t) = (x(t),\ y(t),\ z(t))\), то формула \eqref{ref23} принимает вид
$$
S = \int\limits_{\alpha}^{\beta} \sqrt{(x'(t))^{2}+(y'(t))^{2}+(z'(t))^{2}}\ dt.\label{ref25}
$$
а если \(\Gamma\)-плоская кривая, заданная уравнением
$$
y = f(x),\quad a \leq x \leq b,\nonumber
$$
то ее длина выражается формулой
$$
S = \int\limits_a^b \sqrt{1 + (f^{‘}(x))^{2}}\ dx.\label{ref26}
$$

Пример 6.

Найти длину кривой \(y = \operatorname{ch} x,\ 0 \leq x \leq a\).

\(\triangle\) Применяя формулу \eqref{ref26}, находим
$$
S = \int\limits_0^a \sqrt{1 + \operatorname{sh}^{2}x}\ dx = \int\limits_0^a \operatorname{ch} x\ dx = \operatorname{sh} a.\ \blacktriangle\nonumber
$$

Применение в реальной жизни

Методы расчета объема тела вращения по параметрическим уравнениям имеют широкое применение в различных областях.

В инженерии и архитектуре этот метод используется для проектирования и анализа множества конструкций. Например, при разработке колеса, можно использовать параметрические уравнения для расчета его объема и формы. Это позволяет инженерам оптимизировать геометрию колеса с учетом требуемых характеристик, таких как прочность и сопротивление вращению.

Также в медицине этот метод может быть использован для анализа формы и объема органов или тканей, тем самым помогая в диагностике и планировании операций. Например, при планировании хирургического вмешательства, врачи могут использовать параметрические уравнения для определения объема опухоли или аномалии и определения оптимального подхода к лечению.

Применение методов расчета объема тела вращения по параметрическим уравнениям также может быть найдено в физике, биологии, геометрии и других науках. Например, в физике это может быть использовано для определения объема вращающихся объектов, таких как системы частиц и жидкости, а в биологии — для изучения формы и объема клеток или органов.

Таким образом, методы исчисления объема тела вращения по параметрическим уравнениям имеют широкие практические приложения в различных областях и играют важную роль в проектировании, исследовании и развитии новых технологий и научных открытий.

Физические приложения ОИ

1. Для вычисления пройденного пути в момент времени $t=T$ при переменной скорости движения $v=v\left(t\right)$ материальной точки, которая начала движение в момент времени $t=t_{0} $, используют ОИ $S=\int \limits _{t_{0} }^{T}v\left(t\right)\cdot dt $.
2. Для вычисления работы переменной сили $F=F\left(x\right)$, приложенной к материальной точке, перемещающейся по прямолинейному пути вдоль оси $Ox$ от точки $x=a$ до точки $x=b$ (направление действия силы совпадает с направлением движения) используют ОИ $A=\int \limits _{a}^{b}F\left(x\right)\cdot dx $.
3. Статические моменты относительно координатных осей материальной кривой $y=y\left(x\right)$ на промежутке $\left$ выражаются формулами $M_{x} =\rho \cdot \int \limits _{a}^{b}y\left(x\right)\cdot \sqrt{1+y’^{2} \left(x\right)} \cdot dx $ и $M_{y} =\rho \cdot \int \limits _{a}^{b}x\cdot \sqrt{1+y’^{2} \left(x\right)} \cdot dx $, где линейная плотность $\rho $ этой кривой считается постоянной.
4. Центр масс материальной кривой — это точка, в которой условно сосредоточена вся её масса таким образом, что статические моменты точки относительно координатных осей равны соответствующим статическим моментам всей кривой в целом.

Формулы для вычисления координат центра масс плоской кривой имеют вид $x_{C} =\frac{\int \limits _{a}^{b}x\cdot \sqrt{1+y’^{2} \left(x\right)} \cdot dx }{\int \limits _{a}^{b}\sqrt{1+y’^{2} \left(x\right)} \cdot dx } $ и $y_{C} =\frac{\int \limits _{a}^{b}y\left(x\right)\cdot \sqrt{1+y’^{2} \left(x\right)} \cdot dx }{\int \limits _{a}^{b}\sqrt{1+y’^{2} \left(x\right)} \cdot dx } $.

Статические моменты материальной плоской фигуры в виде КрТ относительно координатных осей выражаются формулами $M_{x} =\frac{1}{2} \cdot \rho \cdot \int \limits _{a}^{b}y^{2} \left(x\right)\cdot dx $ и $M_{y} =\rho \cdot \int \limits _{a}^{b}x\cdot y\left(x\right)\cdot dx $.

Координаты центра масс материальной плоской фигуры в виде КрТ, образованной кривой $y=y\left(x\right)$ на промежутке $\left$, вычисляют по формулам $x_{C} =\frac{\int \limits _{a}^{b}x\cdot y\left(x\right)\cdot dx }{\int \limits _{a}^{b}y\left(x\right)\cdot dx } $ и $y_{C} =\frac{\frac{1}{2} \cdot \int \limits _{a}^{b}y^{2} \left(x\right)\cdot dx }{\int \limits _{a}^{b}y\left(x\right)\cdot dx } $.

Интегрирование по частям и замена переменной

Лимит времени:

из 7 заданий окончено

Вопросы:

1. 1
2. 2
3. 3
4. 4
5. 5
6. 6
7. 7

Информация

Пройдя этот тест, вы закрепите пройденный ранее материал по теме «Интегрирование по частям и замена переменной»

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Результаты

Правильных ответов: из 7

Ваше время:

Время вышло

Вы набрали из баллов ()

Средний результат
Ваш результат

Ваш результат был записан в таблицу лидеров

Капча:

1. 1
2. 2
3. 3
4. 4
5. 5
6. 6
7. 7

1. С ответом

2. С отметкой о просмотре

Вычисление площади поверхности вращения, заданной в прямоугольных координатах

Пусть в прямоугольных координатах на плоскости уравнением y
= f
(x
)

задана кривая, вращением которой вокруг координатной оси образовано тело вращения.

Формула для вычисления площади поверхности вращения следующая:

(1).

Пример 1.
Найти площадь поверхности параболоида, образованную
вращением вокруг оси Ox
дуги параболы
, соответствующей
изменению x
от x
= 0
до
x
= a

.

Решение. Выразим явно функцию, которая задаёт дугу параболы:

Найдём производную этой функции:

Прежде чем воспользоваться формулу для нахождения площади поверхности вращения,
напишем ту часть её подынтегрального выражения, которая представляет собой корень и подставим туда
найденную только что производную:

Ответ: длина дуги кривой равна

.

Пример 2.
Найти площадь поверхности, образуемой вращением
вокруг оси Ox
астроиды
.

Решение. Достаточно вычислить площадь поверхности, получающейся от вращения
одной ветви астроиды, расположенной в первой четверти, и умножить её на 2. Из уравнения астроиды
выразим явно функцию, которую нам нужно будет подставить в формулу для нахождения площади повержности
вращения:

.

Производим интегрирование от 0 до a
:

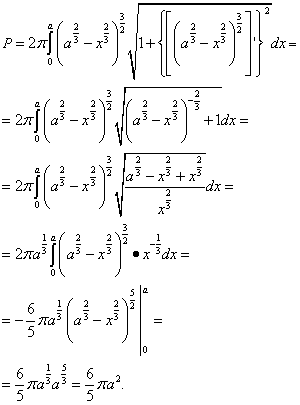
Решаем задачи вместе

Пример 1. Найти объём тела, образованного вращением вокруг оси
абсцисс () фигуры, ограниченной гиперболой
, осью абсцисс и прямыми
, .

Решение. Объём тела вращения найдём по формуле (1), в которой ,
а пределы интегрирования , . Применяем
. Постоянный множитель
выносим за знак интеграла. Получаем:

Пример 2. Найти объём шара радиуса R.

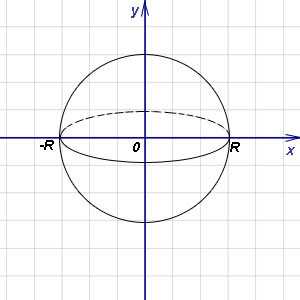
Решение. Рассмотрим шар как тело, получащееся при вращении вокруг оси абсцисс
полукруга радиуса R с центром в начале координат. Тогда в формуле (1) подынтегральная функция
запишется в виде ,
а пределами интегрирования служат -R и R. В вычислениях радиус R считается
константой (вместо него можно подставить любое значение для шара с любым радиусом). Применяем
. Следовательно,

Пример 3. Найти объём тела, образованного вращением вокруг оси
абсцисс () фигуры, заключённой между параболами
и
.

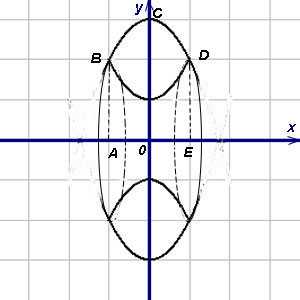
Решение. Представим искомый объём как разность объёмов тел, полученных вращением
вокруг оси абсцисс криволинейных трапеций и .
Объёмы этих тел найдём по формуле (1). В ней пределы интегрирования равны

и —
абсциссам точек B и D пересечения парабол. Эти точки и их абсциссы видны на графике.
Точно также — на графике — можно определить координаты точек пересечения линий из ваших задач. Только
для этого нужно построить график. Теперь можем найти объём тела, применяя
всё тот же табличный интеграл 7:

Пример 4. Вычислить объём тора (тором называется тело, получающееся при вращении круга радиуса a вокруг оси, лежащей в его плоскости на расстоянии b от центра круга (). Форму тора имеет, например, баранка).

Решение. Пусть круг вращается вокруг оси Ox (рис. 20). Объём тора можно представить как разности объёмов тел, полученных от вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Ox.

Уравнение окружности LBCD имеет вид

причём уравнение кривой BCD

а уравнение кривой BLD

Используя разность объёмов тел, получаем для объёма тора v выражение и
вычисляем интеграл:

Пример 5. Найти объём тела, образованного вращением вокруг оси
ординат () фигуры, ограниченной линиями
и
.

Решение. Представим искомый объём как разность объёмов тел, полученных вращением
вокруг оси ординат треугольника и
криволинейной трапеции .
Объёмы этих тел найдём по формуле (2). Пределами интегрирования служат

и —
ординаты точек O и B пересечения параболы и прямой, что видно на графике к этому примеру.
Таким образом, получаем объём тела:

Площадь плоской фигуры

Пусть некоторая плоская фигура в декартовой прямоугольной системе координат $xOy$ сверху ограничена кривой $y=y_{1} \left(x\right)$, снизу — кривой $y=y_{2} \left(x\right)$, а слева и справа вертикальными прямыми $x=a$ и $x=b$ соответственно. В общем случае площадь такой фигуры выражается с помощью ОИ $S=\int \limits _{a}^{b}\left(y_{1} \left(x\right)-y_{2} \left(x\right)\right)\cdot dx $.

Статья: Приложения определенного интеграла

Найди решение своей задачи среди 1 000 000 ответов

Если же некоторая плоская фигура в декартовой прямоугольной системе координат $xOy$ справа ограничена кривой $x=x_{1} \left(y\right)$, слева — кривой $x=x_{2} \left(y\right)$, а снизу и сверху горизонтальными прямыми $y=c$ и $y=d$ соответственно, то площадь такой фигуры выражается с помощью ОИ $S=\int \limits _{c}^{d}\left(x_{1} \left(y\right)-x_{2} \left(y\right)\right)\cdot dy $.

Пусть плоская фигура (криволинейный сектор), рассматриваемая в полярной системе координат, образована графиком непрерывной функции $\rho =\rho \left(\phi \right)$, а также двумя лучами, проходящими под углами $\phi =\alpha $ и $\phi =\beta $ соответственно. Формула для вычисления площади такого криволинейного сектора имеет вид: $S=\frac{1}{2} \cdot \int \limits _{\alpha }^{\beta }\rho ^{2} \left(\phi \right)\cdot d\phi $.

Примеры решения задач

• Пример 1.Найти объем тела вращения вокруг оси абсцисс ограниченного функциями $y=2x-x^2, o<x<2;$Решение

  Выполним чертеж:

  Объем тела вращения:

  $V=\pi\int\limits^a_b f(x)^2\,dx = \pi\int\limits^2_0 (2x-x^2)^2\,dx$ =
  =$\pi\int\limits^2_0 4x^2-4x^3+x^4\,dx = \pi (\frac{32}{3}-16 +\frac{32}{5}) =\frac{ 16\pi}{15}$

• Пример 2.Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры ограниченной линиями $y=2x+1$, $y=x+4$, $x=0$, $x=1$.Решение

  $$V=V_1 — V_2$$

  Найдем фигуру ограниченную сверху прямой $y=x+4$ :

  $$ V_1 = \pi\int\limits^1_0 (x+4)^2\,dx = \pi (\frac{x^3}{3}+4x^2 +16x)|_0^1 =\frac{61\pi}{3}$$

  Найдем фигуру ограниченную сверху прямой $y=2x+1$ :

  $$ V_2 = \pi\int\limits^1_0 (2x+1)^2\,dx = \pi (\frac{4x^3}{3}+2x^2 +x)|_0^1 =\frac{61\pi}{3} =\frac{13\pi}{3}$$
  $$ V = \frac{61\pi}{3} — \frac{13\pi}{3} = 16\pi$$

из 5 заданий окончено

Вопросы:

1. 1
2. 2
3. 3
4. 4
5. 5

Информация

Пройдите этот тест, чтобы проверить свои знания по только что прочитанной теме.

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Результаты

Правильных ответов: из 5

Ваше время:

Время вышло

Вы набрали из баллов ()

Ваш результат был записан в таблицу лидеров

Капча:

1. 1
2. 2
3. 3
4. 4
5. 5

1. С ответом

2. С отметкой о просмотре

1. Задание 1 из 5

   1.

   Количество баллов: 4

   Какая(-ие) формулы для объема тела вращения на промежутке $$ верны:

   • $V=\int\limits^a_b f(x)^2\,dx$

   • $V=\pi\int\limits^a_b f(x)^2\,dx$

   • $V=-\pi\int\limits^b_a f(x)^2\,dx$

   • $V=-\pi\int\limits^a_b f(x)\,dx$

   Правильно
   4 / 4Баллы

   Ответ верный

   Неправильно
   / 4 Баллы

   Попробуйте еще раз

2. Задание 2 из 5

   2.

   Количество баллов: 1

   Вычислить объем тела, полученного вращением фигуры, ограниченной линиями $y=2x-x^2$ , $y=0$ вокруг оси $Ox$ .

   • $\frac{16\pi}{3}$

   • 16

   • $\frac{5}{\pi}$

   Правильно

   Верно, Вы справились с трудной задачей

   Неправильно

   Возможно Вам повезет в следующий раз

3. Задание 3 из 5

   Количество баллов: 1

   Найдите соотвествие

   Элементы сортировки

   • если это ось симметрии фигуры.
   • равен 0.
   • как Ox так и Oy.

   • Ось вращения может и пересекать фигуру

   • Объем тела вращения для функции y=const . На промежутке $a \leq x \leq a$

   • Ось вращения может быть

   Правильно

   Хорошая работа!

   Неправильно

   Всего есть 9 вариантов для создания пары…

4. Задание 4 из 5

   4.

   Количество баллов: 1

   Что такое тор?

   • Декартовое произведение 2х окружностей

   • Геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её

   • Не знаю

   • Геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного

   Правильно

   Слишком легко

   Неправильно

   Попробуйте еще раз

5. Задание 5 из 5

Вывод формулы для площади сферы

Решение . Снова рассмотрим функцию

(4)

графиком которой является верхняя полуокружность радиуса R с центром в начале координат O (рис. 7).

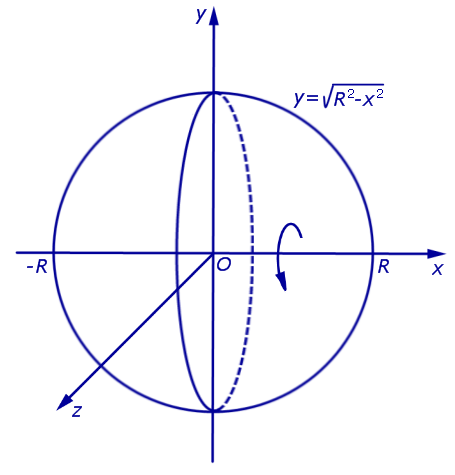
Поскольку сфера радиуса R получается в результате вращения вокруг оси Ox графика функции (4), то в соответствии с формулой для вычисления площади поверхности тела вращения получаем

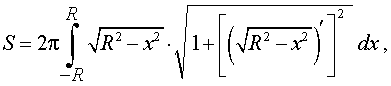
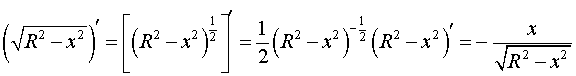
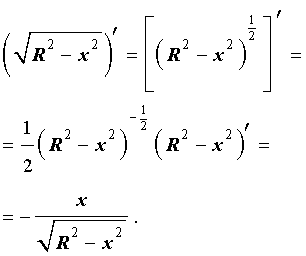
Подставим найденную производную в выражение, стоящее под знаком квадратного корня:

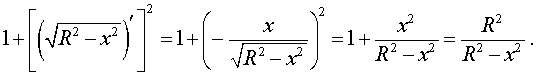
Таким образом, подынтегральная функция принимает вид:

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Сегодня на уроке мы выведем формулу для вычисления объема тела при помощи определенного интеграла и применения формулы к решению задачи.

Вспомним, что называется определенным интегралом.

Если функция f(x) непрерывна на промежутке I числовой оси, содержащей точки х=а и х=b, то разность значений F(b)-F(a) (где F(x) — первообразная f(x) на I) называется определенным интегралом от функции f(x) от a до b.

Это формула получила название Ньютона-Лейбница.

(интеграл от a до b эф от икс дэ икс равен разности значений первообразной эф большое от бэ и а)

Выведем основную формулу для вычисления объемов тел, основанную на понятии интеграла: объем тела равен интегралу от а до b площади основания фигуры дэ икс,

Будем рассматривать произвольное тело объёмом V, заключенное между двумя параллельными плоскостями которая перпендикулярна данным плоскостям.