Объем цилиндра

Факторы, влияющие на диаметр цилиндра

Фактор	Влияние на диаметр цилиндра
Мощность двигателя	Чем больше мощность двигателя, тем чаще требуется более крупный диаметр цилиндра для обеспечения эффективной работы и достижения высоких показателей.
Вращающий момент	Высокий вращающий момент может потребовать увеличения диаметра цилиндра для обеспечения достаточной прочности и избежания деформаций.
Скорость вращения	При повышенной скорости вращения двигателя может потребоваться уменьшение диаметра цилиндра для достижения оптимального соотношения между скоростью и мощностью.
Тип работы	Различные типы работы (например, рабочий или холостой ход, непрерывная нагрузка или временные пики) могут требовать различных диаметров цилиндров для обеспечения оптимальной производительности и надежности.
Материалы и технологии	Использование конкретных материалов и технологий может оказывать влияние на требуемый диаметр цилиндра в связи с их свойствами, например, прочностью, теплоотводом и износостойкостью.

Определение оптимального диаметра цилиндра требует тщательного анализа всех факторов, которые могут повлиять на его работу и производительность. Правильный выбор диаметра цилиндра позволяет добиться эффективности работы, увеличить срок службы и минимизировать возможные проблемы и поломки.

Примеры расчетов диаметра цилиндра

Для расчета диаметра цилиндра необходимо знать другие параметры, такие как его объем или площадь основания.

Пример 1:

1. Известен объем цилиндра, равный 1256 кубическим сантиметрам.
2. Формула для расчета объема цилиндра: V = π * r^2 * h, где V — объем, r — радиус основания, h — высота.
3. Так как нам известен объем и требуется найти диаметр, используем формулу для нахождения радиуса: r = √(V / (π * h)).
4. Подставляем значения: r = √(1256 / (π * h)).
5. Допустим, что высота цилиндра равна 10 сантиметрам.
6. Подставляем значения: r = √(1256 / (π * 10)).
7. Вычисляем радиус: r ≈ √39.92 ≈ 6.31.
8. Так как диаметр равен удвоенному радиусу, умножаем полученное значение на 2: d ≈ 6.31 * 2 ≈ 12.62 сантиметра.
9. Диаметр цилиндра составляет приближенно 12.62 сантиметра.

Пример 2:

• Известна площадь основания цилиндра, равная 100 квадратным метрам.
• Формула для расчета площади основания цилиндра: S = π * r^2, где S — площадь, r — радиус основания.
• Так как нам известна площадь основания и требуется найти диаметр, используем формулу для нахождения радиуса: r = √(S / π).
• Подставляем значения: r = √(100 / π).
• Вычисляем радиус: r ≈ √31.83 ≈ 5.64.
• Так как диаметр равен удвоенному радиусу, умножаем полученное значение на 2: d ≈ 5.64 * 2 ≈ 11.28 метра.
• Диаметр цилиндра составляет приближенно 11.28 метра.

Важно помнить, что формулы и методы расчета могут различаться в зависимости от условий задачи и известных параметров

Калькулятор для цилиндра

Онлайн калькулятор для цилиндра позволяет по известным данным вычислить:

• объем цилиндра,
• площадь основания, площадь боковой поверхности и площадь полной поверхности цилиндра,
• элементы: радиус, диаметр и высоту.

Калькулятор для цилиндра: комментарий

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра).

Обозначения для цилиндра:R – радиус, D – диаметр, V – объем, Sо – площадь основания, Sб – площадь боковой поверхности, S – площадь полной поверхности,h – высота прямого кругового цилиндра (h1 и h2 — минимальная и максимальная высота)π – число Пи которое всегда примерно равно 3,14.

Прямой круговой цилиндр

Круговым называется цилиндр, если его направляющая является окружностью. Прямым называется цилиндр, если его образующая перпендикулярна основаниям.

Формулы для прямого кругового цилиндра:

Найти объем цилиндра , если известны:

• радиус и высота цилиндра: V=πR 2 h
• диаметр и высота цилиндра: V=πD 2 /4h
• площадь и высота цилиндра: V=Sоh

Площадь(Sб) боковой поверхности прямого кругового цилиндра

Так как боковая поверхность представляет собой прямоугольник, то площадь боковой поверхности цилиндра определяется по формуле: Sб=2πR⋅h

Площадь(Sо) основания цилиндра

Основание цилиндра —круг, поэтому площадь одного основания находится по формуле площади круга: Sо=πR 2 .

Площадь(S) полной поверхности прямого кругового цилиндра

Площадь полной поверхности цилиндра определяется по формуле: S=2πRh+2πR 2 =2πR(h+R)

Формулы нахождения радиуса и диаметра по:

• высоте и объему: R=√(V/πh) , D=2*√(V/πh)
• площади боковой поверхности и высоте: R=Sб/2πh , D=2*Sб/2πh
• площади основания и высоте: R=√(Sо/π) , R=2*√(Sо/π)

Формулы нахождения высоты по:

• радиусу и объему: h=V/πR 2
• площади боковой поверхности и радиусу: h=Sб/2πR
• площади полной поверхности и радиусу: h=S/2πR-R

Скошенный цилиндр

Прямой круговой цилиндр со скошенным основанием (скошенный цилиндр) определяется радиусом основания R, минимальной высотой h1 и максимальной высотой h2.

Источник

Геометрическое Описание Цилиндра

Цилиндр представляет собой трехмерную геометрическую фигуру, характеризующуюся двумя параллельными и равными основаниями, соединенными боковой поверхностью. Вот ключевые характеристики цилиндра:

Основания

• Форма: Круглая (в случае прямого кругового цилиндра) или эллиптическая (для эллиптического цилиндра).
• Расположение: Параллельно друг другу на равном расстоянии.

Боковая Поверхность

Форма: Прямоугольник, обернутый вокруг оси цилиндра. В прямом цилиндре боковая поверхность перпендикулярна основаниям.

Высота (h)

Описание: Перпендикулярное расстояние между двумя основаниями.

Важность: Определяет длину боковой поверхности.

Радиус (r) и Диаметр (d)

• Радиус: Расстояние от центра основания до его края.
• Диаметр: Двойной радиус, наибольшее расстояние через центральную точку основания.

Ось Цилиндра

• Описание: Воображаемая линия, соединяющая центры оснований.
• Роль: Определяет направление и ориентацию цилиндра.

Таблица Характеристик Цилиндра

Характеристика	Описание
Основания	Два параллельных круга разного радиуса
Боковая поверхность	Наклонная, состоит из образующих
Высота (h)	Перпендикулярное расстояние между основаниями
Радиусы (R и r)	Радиусы большего и меньшего оснований соответственно
Образующая (l)	Расстояние между краями оснований

Примеры задач на расчет площади поверхности цилиндра

Пример 1

Найти площадь поверхности цилиндра, если его высота равна 10 см, а радиус основания равен 5 см.

Площадь боковой поверхности цилиндра равна 2πrh, где r – радиус основания цилиндра, h – высота цилиндра.

Подставляем значения: 2π * 5 см * 10 см = 100π см^2.

Площадь основания цилиндра равна πr^2. Подставляем значения: π * (5 см)^2 = 25π см^2.

Площадь поверхности цилиндра равна сумме площади боковой поверхности и площади двух оснований: 100π см^2 + 2 * 25π см^2 = 150π см^2.

Ответ: площадь поверхности цилиндра равна 150π см^2.

Пример 2

Найти площадь поверхности цилиндра, если его высота равна 3 см, а площадь основания равна 4π кв.см.

Для начала найдем радиус основания цилиндра по формуле S = πr^2.

4π кв.см = πr^2. Решаем уравнение: r = √(4) = 2 см.

Площадь боковой поверхности цилиндра равна 2πrh, где r – радиус основания цилиндра, h – высота цилиндра.

Подставляем значения: 2π * 2 см * 3 см = 12π см^2.

Площадь поверхности цилиндра равна сумме площади боковой поверхности и площади двух оснований: 12π см^2 + 2 * 4π см^2 = 20π см^2.

Ответ: площадь поверхности цилиндра равна 20π см^2.

Пример 3

Найти площадь поверхности полого цилиндра, если его наружный радиус равен 8 см, внутренний радиус – 5 см, высота – 12 см.

Площадь боковой поверхности цилиндра равна (r1 + r2)h, где r1 – наружный радиус цилиндра, r2 – внутренний радиус цилиндра, h – высота цилиндра.

Подставляем значения: (8 см + 5 см) * 12 см = 156 см^2.

Найдем площадь наружной поверхности цилиндра: 2πr1h = 2π * 8 см * 12 см = 192π см^2.

Найдем площадь внутренней поверхности цилиндра: 2πr2h = 2π * 5 см * 12 см = 120π см^2.

Площадь поверхности полого цилиндра равна сумме площади боковой поверхности, площади наружной поверхности и площади внутренней поверхности: 156 см^2 + 192π см^2 — 120π см^2 = 156 см^2 + 72π см^2 = 156 + 226,2 ≈ 382,2 (см^2).

Ответ: площадь поверхности полого цилиндра равна примерно 382,2 см^2.

Формулы расчёта объёма цилиндра

Объем правильного цилиндра через радиус и высоту

Формула расчёта объема правильного цилиндра через радиус и высоту Вам необходимо указать радиус основания цилиндра (r) и высота цилиндра (h).
Онлайн калькулятор делает расчёт по формуле: V=pi*r2*h .

Посчитать

Объём полого цилиндра

Формула расчёта: V = pi*(r1-r2)*h

Посчитать

Формула расчёта:

Посчитать

По внутреннему диаметру и толщине стенки

Формула расчёта: V = pi*(d*δ+δ2)*h

Посчитать

Через площадь основания и высоту

Формула расчёта объема правильного цилиндра через площадь основания и высоту Вам необходимо указать площадь основания цилиндра (S) и высота цилиндра (h).
Онлайн калькулятор делает расчёт по формуле: V=S*h.

Посчитать

Через диаметр основания и высоту

Формула расчёта объема правильного цилиндра через диаметр основания и высоту Вам необходимо указать диаметр основания цилиндра (d) и высота цилиндра (h).
Онлайн калькулятор делает расчёт по формуле: V=pi*d2/4*h.

Посчитать

Через диаметр основания и высоту

Формула расчёта: V = (α°/360)*pi*r2*h

Посчитать

Как узнать объем цилиндра?

Объем цилиндра – это количество пространства, занимаемого цилиндром. Он вычисляется по формуле V=πr²h, где π (пи)– математическая константа, примерное значение которой равно 3,14; r – радиус основания цилиндра; h – высота цилиндра.

Чтобы узнать объем цилиндра, необходимо знать его радиус и высоту. Если они неизвестны, их можно измерить. В случае, если цилиндр имеет нестандартную форму, например, эллиптический сечение в нескольких местах, вычисление объема будет затруднительным, и, возможно, потребуется помощь специалиста.

Чтобы измерить радиус цилиндра, можно взять линейку или измерительную ленту и, затем, измерить расстояние от центра основания цилиндра до края окружности. Высота цилиндра измеряется от основания до вершины. Ее можно также измерить с помощью линейки или измерительной ленты.

Также можно использовать формулу, выражающую радиус через диаметр цилиндра – r = d/2, где d – диаметр основания цилиндра. Затем останется только подставить значения радиуса и высоты в формулу для вычисления объема, и вы получите ответ в кубических метрах (м³) или кубических сантиметрах (см³).

Таким образом, для того чтобы узнать объем цилиндра, вам необходимо измерить радиус и высоту его основания и применить формулу V = πr²h.

Широкое применение цилиндров в повседневной жизни

Цилиндр — это геометрическое тело, которое может использоваться в различных областях. Ниже приведены некоторые примеры использования цилиндра:

1. Создание двигателей внутреннего сгорания: таких как двигатель автомобиля или мотоцикла.
2. Механика: например в гидравлических цилиндрах, которые используются для перемещения или прессования тяжелых предметов.
3. Создание емкостей: таких как баки для хранения газа или жидкости.
4. Столярное дело: для создания столбов, колонн или других элементов архитектуры.
5. Математика: для решения геометрических задач и для вычисления объемов и площадей тел.
6. Кулинария: для формирования булочек, пирогов, кексов и других блюд.
7. Сосуды для хранения и транспортировки жидкостей: таких как газы, масла, смазки и прочее.
8. Научные исследования: например для измерения давления, температуры и других параметров.

Вопросы и ответы

Обратите внимание на ответы на некоторые часто задаваемые вопросы

Какова формула для вычисления площади цилиндра?

Формула для вычисления площади цилиндра зависит от того, какую площадь вы хотите найти. Обычно вычисляют площадь боковой поверхности и площадь полной поверхности цилиндра. Для нахождения площади боковой поверхности цилиндра используйте формулу 2πrh, где r — радиус цилиндра, а h — его высота. Для нахождения площади полной поверхности цилиндра нужно прибавить к площади боковой поверхности удвоенную площадь оснований, т.е. используйте формулу 2πrh + 2πr^2.

Как использовать онлайн калькулятор для вычисления площади цилиндра?

Чтобы использовать онлайн калькулятор для вычисления площади цилиндра, вам нужно ввести значения радиуса и высоты цилиндра в соответствующие поля. Затем онлайн калькулятор автоматически рассчитает площадь цилиндра.

Как найти радиус цилиндра, если известна его площадь?

Для нахождения радиуса цилиндра по известной площади необходимо использовать формулу S = 2πrh + 2πr^2, где S — площадь цилиндра, r — радиус цилиндра, h — его высота. После подстановки известных значений в формулу можно найти радиус цилиндра.

Нет, онлайн калькулятор площади цилиндра предназначен только для вычисления площади цилиндра. Для вычисления площади других геометрических фигур необходимо использовать соответствующие калькуляторы.

Онлайн калькулятор площади цилиндра не имеет ограничений на значения радиуса и высоты, которые можно ввести. Однако, для более точных результатов, рекомендуется использовать реалистичные значения.

Результаты вычислений, полученные с помощью онлайн калькулятора площади цилиндра, можно использовать для решения различных задач, связанных с геометрией, например, для расчета объема цилиндра, для определения необходимого количества материала для изготовления цилиндрического объекта или для определения количества жидкости, которая может поместиться в цилиндрический резервуар.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
• Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
• Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
• Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
• Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
• Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
• Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
• Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
• Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
• Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.

Осевое сечение наклонного цилиндра

Рисунок выше демонстрирует наклонный цилиндр, изготовленный из бумаги. Если выполнить его осевое сечение, то получится уже не прямоугольник, а параллелограмм. Его стороны – это известные величины. Одна из них, как и в случае сечения прямого цилиндра, равна диаметру d основания, другая же – длина образующего отрезка. Обозначим ее b.

Для однозначного определения параметров параллелограмма недостаточно знать его длины сторон. Необходим еще угол между ними. Предположим, что острый угол между направляющей и основанием равен α. Он же и будет углом между сторонами параллелограмма. Тогда формулу для площади осевого сечения наклонного цилиндра можно записать следующим образом:

Диагонали осевого сечения цилиндра наклонного рассчитать несколько сложнее. Параллелограмм имеет две диагонали разной длины. Приведем без вывода выражения, позволяющие рассчитывать диагонали параллелограмма по известным сторонам и острому углу между ними:

l1 = √(d2 + b2 – 2*b*d*cos(α));

l2 = √(d2 + b2 + 2*b*d*cos(α))

Здесь l1 и l2 – длины малой и большой диагоналей соответственно. Эти формулы можно получить самостоятельно, если рассмотреть каждую диагональ как вектор, введя прямоугольную систему координат на плоскости.

ما هو القطر لأساس اسطوانة؟

المقدمة:

الأسطوانة هي هندسة أساسها دائرة وجسمها طويل ومستقيم الشكل. يتكون الأسطوانة من قاعدتين دائريتين وجسم مستقيم يربط بينهما. يمكن حساب القطر لأساس الأسطوانة بأكثر من طريقة ، وسنشرح طريقة بسيطة وسريعة لحساب ذلك.

كيف يمكن حساب القطر لأساس الأسطوانة؟

عندما يتم إعطاء مساحة قاعدة الأسطوانة ، يمكن استخدام هذا الرابط لحساب قطر الأساس:

القطر = جذر (4 × مساحة القاعدة ÷ القيمة الثابتة باي (π) )

• الخطوة ١: ضرب مساحة القاعدة ب 4
• الخطوة ٢: تقسيم الناتج السابق على القيمة الثابتة باي (π)
• الخطوة ٣: أخذ الجذر التربيعي للناتج السابق للحصول على القطر

مثال على حساب القطر لأساس الأسطوانة:

لنفترض أننا نريد حساب القطر لأساس الأسطوانة التي لديها مساحة قاعدة تبلغ 50 متر مربع. نستخدم الرابط أعلاه لحل هذه المسألة ، بالترتيب:

• الخطوة ١: (4 × 50) = 200
• الخطوة ٢: 200 ÷ 3.14 ≈ 63.7
• الخطوة ٣: الجذر التربيعي لـ 63.7 ≈ 8

لذلك ، فإن قطر الأساس هو 8 متر.

❓ Вопросы и ответы

Сейчас мы представим ответы на вопросы, которые часто возникают по данной теме.

Что такое цилиндр?

Цилиндр — это геометрическая фигура, которая имеет два плоских основания, обычно круглой формы, и боковую поверхность, которая состоит из параллельных прямых линий.

Как вычислить объем цилиндра?

Объем цилиндра можно вычислить, используя формулу:

V = πr²h

где V — объем цилиндра, π — число Пи (приблизительно равно 3.14), r — радиус основания цилиндра и h — высота цилиндра.

Можно ли использовать формулу объема цилиндра для вычисления объема других фигур?

Нет, формула объема цилиндра может использоваться только для вычисления объема цилиндра. Для других фигур существуют свои собственные формулы для расчета объема.

Как найти радиус или диаметр цилиндра, если они неизвестны?

Если известна площадь основания цилиндра, можно найти радиус, используя формулу:

r = √(A/π)

где A — площадь основания цилиндра.

Если известен объем цилиндра, можно найти радиус, используя формулу:

r = √(V/πh)

где V — объем цилиндра, h — высота цилиндра.

Диаметр можно найти, удваивая радиус.

Как найти объем трубы или канала?

Для трубы или канала формула для вычисления объема имеет немного другой вид:

V = πr²h

где V — объем, r — радиус, h — длина (высота) трубы или канала.

Например, если радиус трубы равен 10 см, а длина трубы составляет 2 м, то объем трубы будет:

V = 3.14 * 10² * 200 = 62,800 см³, что равно 62.8 литрам.

Как узнать, сколько литров вмещает бочка?

Чтобы узнать, сколько литров вмещает бочка, нужно знать ее объем. Если известны диаметр и высота бочки, то можно использовать формулу для объема цилиндра. Например, если диаметр бочки составляет 1 метр, а высота — 1,5 метра, то ее объем будет:

V = πr²h = 3.14 * (1/2)² * 1.5 = 1.18 кубических метров, что равно 1180 литрам. Таким образом, бочка вмещает 1180 литров жидкости.

Как узнать, сколько литров вмещает труба?

Для расчета объема трубы нужно знать ее длину и радиус. Если известны диаметр и длина трубы, то радиус можно найти, разделив диаметр на 2. Например, если диаметр трубы составляет 10 см, а длина трубы — 2 метра, то радиус будет 5 см. Тогда объем трубы можно найти, используя формулу:

V = πr²h = 3.14 * (5/100)² * 200 = 15.7 литров. Таким образом, труба вмещает 15.7 литров жидкости.

Какой тип калькулятора нужен для расчета объема цилиндра?

Для расчета объема цилиндра нужен специальный калькулятор, который может выполнить математические операции с использованием формулы для объема цилиндра.

Какие дополнительные функции могут быть включены в калькулятор объема цилиндра?

Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.

Как измерить диаметр цилиндра

Первый способ — использовать микрометр. Микрометр — это точный инструмент для измерения малых длин, который позволяет измерять диаметр цилиндра с высокой точностью

Чтобы измерить диаметр, поместите микрометр вокруг цилиндра и осторожно закройте винт, пока измерительные челюсти плотно прижимаются к поверхности. Затем прочитайте значение размера на шкале микрометра

Второй способ — использовать линейку или измерительную ленту. Этот метод подходит для грубого измерения диаметра цилиндра, но может иметь большую погрешность. Поместите линейку или измерительную ленту на противоположные стороны цилиндра и прочитайте значение на шкале.

Третий способ — использовать калиперы. Калиперы — это инструмент, используемый для измерения длин, ширин и глубины

Чтобы измерить диаметр цилиндра с помощью калиперов, поместите их на противоположные стороны цилиндра и осторожно закройте их, чтобы измерительные концы прижались к поверхности. Затем прочитайте значение размера на шкале калиперов

Метод	Преимущества	Недостатки
Микрометр	Высокая точность измерений	Требует специального инструмента
Линейка/измерительная лента	Простота использования	Большая погрешность измерений
Калиперы	Можно измерять различные параметры	Менее точные результаты, чем с использованием микрометра

Выбор метода измерения диаметра цилиндра зависит от требуемой точности и имеющихся инструментов

Важно помнить, что для получения наиболее точных результатов необходимо проводить измерения несколько раз и усреднять полученные значения

Способ расчета радиуса цилиндра:

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности. Формула радиуса цилиндра:

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности. Формула радиуса цилиндра:

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности. Формула радиуса цилиндра:

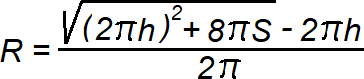
S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr2=πr (2h+r)

R = √V / πh

где V — объем цилиндра, h — высота.Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:

Практические рекомендации

Если необходимо найти диаметр основания цилиндра, следует воспользоваться формулой, которая связывает диаметр с радиусом и общей площадью основания: D = 2r = √(4S/π).

Для начала необходимо измерить общую площадь основания цилиндра. Это можно сделать с помощью рулетки или линейки. Если же основание имеет необычную форму, то можно воспользоваться формулами, позволяющими вычислить площадь треугольника, прямоугольника или многоугольника.

Затем следует вычислить радиус основания, разделив площадь на π и извлекая из полученного числа квадратный корень. Наконец, умножив радиус на 2, можно найти диаметр основания цилиндра.

Важно помнить, что все измерения должны быть проведены с высокой точностью, чтобы избежать ошибок в расчетах.
Если основание цилиндра имеет сложную форму, можно разбить его на более простые геометрические фигуры и вычислить площадь каждой из них отдельно.
Проверить правильность результатов можно, сравнив диаметр, найденный по формуле, с фактическим диаметром, полученным путем измерений.

Если возникают трудности в вычислении диаметра, можно воспользоваться онлайн калькулятором, который самостоятельно выполнит все необходимые расчеты и выведет результат на экран.

Вопрос-ответ

Вопрос: Как найти диаметр основания цилиндра, если известен объем?

Ответ: Для вычисления диаметра необходимо использовать формулу диаметра основания цилиндра по объему: d = 2 * √(V/πh), где d — диаметр, V — объем, h — высота цилиндра. Подставляем известные значения и получаем диаметр.

Вопрос: Как найти диаметр основания цилиндра, если известны его объем и высота?

Ответ: Для вычисления диаметра необходимо использовать формулу диаметра основания цилиндра по объему: d = 2 * √(V/πh), где d — диаметр, V — объем, h — высота цилиндра. Подставляем известные значения и получаем диаметр.

Вопрос: Как найти диаметр основания цилиндра, если известна площадь его боковой поверхности?

Ответ: Для вычисления диаметра необходимо использовать формулу диаметра основания цилиндра по боковой поверхности: d = 2 * h * (S/2πh), где d — диаметр, S — площадь боковой поверхности, h — высота цилиндра. Подставляем известные значения и получаем диаметр.

Вопрос: Как найти диаметр основания цилиндра, если известны его объем и радиус?

Ответ: Для вычисления диаметра необходимо использовать формулу диаметра основания цилиндра по радиусу и объему: d = 2 * (√(4V/π) — r), где d — диаметр, V — объем, r — радиус основания цилиндра. Подставляем известные значения и получаем диаметр.

Вопрос: Как найти диаметр основания цилиндра, если известны его площадь основания и высота?

Ответ: Для вычисления диаметра необходимо использовать формулу диаметра основания цилиндра по площади основания и высоте: d = √(4S/πh), где d — диаметр, S — площадь основания, h — высота цилиндра. Подставляем известные значения и получаем диаметр.

Главная — Онлайн — Новичкам в математике: как определить диаметр основания цилиндра без напряжения

Комментарии

JohnSmith

5.0 out of 5.0 stars5.0

Спасибо за быструю и понятную инструкцию! Теперь знаю, как найти диаметр основания цилиндра.

ChristopherDavis
5.0 out of 5.0 stars5.0

NikitaM
5.0 out of 5.0 stars5.0

Статья очень помогла, нашел ответ за 2 минуты. Спасибо!

Алексей
5.0 out of 5.0 stars5.0

Я всегда думал, что поиск диаметра основания цилиндра — это что-то сложно и запутанное. Но после того, как прочитал эту статью, мне стало все ясно. Спасибо за простую и доступную инструкцию. Теперь я смогу самостоятельно решить подобные задачи без проблем.

MichaelWilliams
5.0 out of 5.0 stars5.0

Сергей
5.0 out of 5.0 stars5.0

Я всегда считал, что математика — это не мое. И тем более, когда речь заходит об определении диаметра основания цилиндра — мне казалось, что это что-то сложное и запутанное. Тем не менее, после того, как я прочитал эту статью, я стал на много увереннее в своих способностях.

Рассмотренная в статье формула для расчета диаметра основания цилиндра оказалась настолько простой и понятной, что даже я в силах был ее освоить

Теперь я понимаю, что безумно важно не бояться новых задач и пробовать решать их самостоятельно

Спасибо авторам за качественный и доступный материал. Я считаю, что статьи такого формата помогают многим людям развиваться и учиться новому.

Что такое объем

Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм3, см3, мл3.

Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.

Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.

Объем и площадь других видов цилиндров рассмотрен в статьях: