Площадь цилиндра калькулятор онлайн

Формулы вычисления радиуса цилиндра

1. Через объем и высоту

Радиус цилиндра рассчитывается по формуле:

V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.

• R – радиус основания цилиндра, т.е. окружности;
• π – число, округленное значение которого равняется 3,14.

2. Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

S_бок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:

3. Через полную площадь поверхности

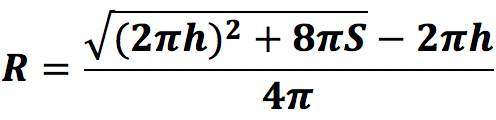
Данная формула получена следующим образом:

S – полная площадь поверхности фигуры, равная:

S = 2 π Rh + 2 π R 2 или S = 2 π R(h + R)

Возьмем первое выражение. Если перенести S в правую часть, получим:

2 π R 2 + 2 π Rh – S = 0

Можно заметить, что это квадратное уравнение вида ax 2 + bx + c = 0, где:

R является корнем данного уравнения (x). Подставив в стандартную формулу для расчета корней наши значения a, b и с получаем*:

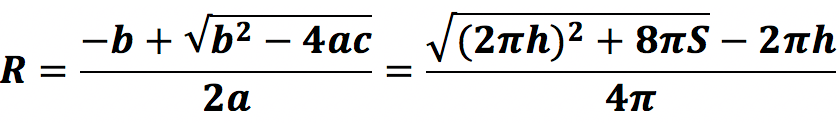
* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.

Excel 4. Содержимое ячеек – Эффективная работа в MS Office

1. В ячейке A1 вычисляется сумма значений ячеек B1 и C1 – аргумент a=1.
2. В ячейке A2 вычисляется разность значений ячеек B2 и C2 – аргумент a=2.
3. В ячейке A3 вычисляется произведение значений ячеек B3 и C3 – аргумент a=3.

В этом примере мы не присваиваем пользовательской функции значение, поэтому отображается значение по умолчанию – 0. Если объявить эту функцию как строковую: Function Primer1(Cell1 As Range, Cell2 As Range) as String , будет возвращена пустая строка.

Заливка ячеек цветом

Есть два способа изменить цвет заливки выделенных ячеек:

VBA Excel. Изменение значений других ячеек из функции
Он заключается в добавлении дополнительного аргумента в пользовательскую функцию, с помощью которого для каждой ячейки можно вывести отдельный результат. Функция размещается в каждой изменяемой ячейке.

Редактирование диаграмм

Закончив построение диаграмм, их можно изменить в любой момент. Одновременно с появившейся диаграммой автоматически возникает группа вкладок с общим названием «Работа с диаграммами», и происходит переход на первую из них – «Конструктор». Инструменты новых вкладок открывают широкие возможности редактирования диаграмм.

Вкладка «Конструктор»

Для отображения значений процентов часто применяется круговая диаграмма в эксель. Чтобы нарисовать круговую диаграмму, сохранив прежние данные, нужно щёлкнуть первый слева инструмент линейки – «Изменить тип диаграммы», и выбрать желаемый подвид строки «Круговая».

На следующем скриншоте показан результат активации инструмента «Строка/Столбец», производящий взаимную замену данных на осях X и Y. Как видно, однотонная гистограмма предыдущего скриншота получила цвета, и стала гораздо привлекательней.

В разделе «Стили диаграмм» вкладки «Конструктор» можно менять стиль диаграмм. После открытия выпадающего списка этого раздела пользователю становится доступным выбор одного из 40 предлагаемых вариаций стилей. Без открытия этого списка доступно всего 4 стиля.

Очень ценен последний инструмент – «Переместить диаграмму». С его помощью диаграмму можно перенести на отдельный полноэкранный лист.

Как видно, лист с диаграммой добавляется к существовавшим листам.

Если пользователю предстоит работа по построению множества других диаграмм на основе созданной и отредактированной, то он может сохранить её для дальнейшего использования в качестве шаблона. Для этого достаточно выделить диаграмму, щёлкнуть инструмент «Сохранить как шаблон», ввести название и нажать «Сохранить». После этого запомненный шаблон будет доступен в папке «Шаблоны».

Вкладки «Макет» и «Формат»

Инструменты вкладок «Макет» и «Формат» в основном относятся к внешнему оформлению диаграммы.

Чтобы добавить название, следует щёлкнуть «Название диаграммы», выбрать один из двух предлагаемых вариантов размещения, ввести имя в строке формул, и нажать Enter.

При необходимости аналогично добавляются названия на оси диаграммы X и Y.

Инструмент «Легенда» управляет отображением и положением поясняющего текста. В данном случае это – названия месяцев. Их можно удалить или переместить влево, вверх или вниз.

Гораздо более употребителен инструмент «Подписи данных», позволяющий добавить на них числовые значения.

Если при построении диаграммы был выбран её объёмный вариант, то на вкладке «Макет» будет активен инструмент «Поворот объёмной фигуры». С его помощью можно менять угол наблюдения диаграммы.

Инструмент «Заливка фигуры» вкладки «Формат» позволяет залить любым цветом, рисунком, градиентом или текстурой фон диаграммы (как показано на скриншоте) или любой из её элементов (в данном случае – столбиков).

Для заливки соответствующего элемента он должен быть предварительно выделен.

Добавление новых данных

После создания диаграммы для одного ряда данных в некоторых случаях бывает необходимо добавить на диаграмму новые данные. Для этого сначала нужно будет выделить новый столбик – в данном случае «Налоги», и запомнить его в буфере обмена, нажав Ctrl+C. Затем щёлкнуть на диаграмме, и добавить в неё запомненные новые данные, нажав Ctrl+V. На диаграмме появится новый ряд данных «Налоги».

Новые возможности диаграмм в Excel 2013

Диаграммы рассматривались на примере широко распространённой версии Excel 2010. Так же можно работать и в Excel 2007. А вот версия 2013 года имеет ряд приятных нововведений, облегчающих работу с диаграммами:

• в окне вставки вида диаграммы введён её предварительный просмотр в дополнение к маленькой иконке;
• в окне вставки вида появился новый тип – «Комбинированная», сочетающий несколько видов;
• в окне вставки вида появилась страница «Рекомендуемые диаграммы», которые версия 2013 г. советует, проанализировав выделенные исходные данные;
• вместо вкладки «Макет» используются три новые кнопки – «Элементы диаграммы», «Стили диаграмм» и «Фильтры диаграммы», назначение которых ясно из названий;
• настройка дизайна элементов диаграммы производится посредством удобной правой панели вместо диалогового окна;
• подписи данных стало возможным оформлять в виде выносок и брать их прямо с листа;
• при изменении исходных данных диаграмма плавно перетекает в новое состояние.

Примеры вычисления:

Задача: Найдите площадь круга радиус которого равен 9 см.

Решение: S = πR2 = 3.14 * 92 = 3.14 * 81 ≈ 254.34 см2

Ответ: 254.34 см2

Задача: Найдите площадь круга радиус которого равен 4 см.

Решение: S = πR2 = 3.14 * 42 = 3.14 * 16 ≈ 50.24 см2

Ответ: 50.24 см2

Задача: Найдите площадь круга радиус которого равен 8 см.

Решение: S = πR2 = 3.14 * 82 = 3.14 * 64 ≈ 200.96 см2

Ответ: 200.96 см2

Задача: Найдите площадь круга радиус которого равен 7 см.

Решение: S = πR2 = 3.14 * 72 = 3.14 * 49 ≈ 153.86 см2

Ответ: 153.86 см2

Задача: Найдите площадь круга радиус которого равен 3 см.

Решение: S = πR2 = 3.14 * 32 = 3.14 * 9 ≈ 28.26 см2

Ответ: 28.26 см2

Задача: Найдите площадь круга радиус которого равен 5 см.

Решение: S = πR2 = 3.14 * 52 = 3.14 * 25 ≈ 78.5 см2

Ответ: 78.5 см2

Задача: Найдите площадь круга радиус которого равен 33 см.

Решение: S = πR2 = 3.14 * 332 = 3.14 * 1089 ≈ 3419.46 см2

Ответ: 3419.46 см2

Задача: Найди площадь круга диаметр которого равен 10 см.

Решение: S = 14πd2 = 14 * 3.14 * 102 = 3144 ≈ 78.5 см2

Ответ: 78.5 см2

Задача: Найди площадь круга диаметр которого равен 1010 см.

Решение: S = 14πd2 = 14 * 3.14 * 10102 = 3.14 * 10201004 ≈ 800778.5 см2

Ответ: 800778.5 см2

Задача: Найди площадь круга диаметр которого равен 6 см.

Решение: S = 14πd2 = 14 * 3.14 * 62 = 3.14 * 364 ≈ 28.26 см2

Ответ: 28.26 см2

Задача: Найдите площадь круга если его диаметр равен 22 м.

Решение: S = 14πd2 = 14 * 3.14 * 222 = 3.14 * 4844 ≈ 379.94 м2

Ответ: 379.94 м2

Задача: Найдите площадь круга если его диаметр равен 24 см.

Решение: S = 14πd2 = 14 * 3.14 * 242 = 3.14 * 5764 ≈ 452.16 см2

Ответ: 452.16 см2

Задача: Найдите площадь круга если длина окружности равна 5 см.

Решение: S = C24π = 524 * 3.14 = 254 * 3.14 ≈ 1.99 см2

Ответ: 1.99 см2

Задача: Длина окружности равна 40 см найдите площадь круга.

Решение: S = C24π = 4024 * 3.14 = 16004 * 3.14 ≈ 127.39 см2

Ответ: 127.39 см2

Задача: Длина окружности равна 15 м найдите площадь круга.

Решение: S = C24π = 1524 * 3.14 = 2254 * 3.14 ≈ 17.91 м2

Ответ: 17.91 м2

Формула расчета площади круга

Основные определения

Окружность — это геометрическая фигура, состоящая из всех точек в плоскости, которые находятся на одинаковом расстоянии от центра окружности. Расстояние между центром окружности и любой ее точкой называется радиусом окружности. Окружность не имеет внутренней части, она представляет только границу круга.

Круг — это часть плоскости, состоящая из всех точек окружности и всех точек внутри окружности.

Радиус — это отрезок, который соединяет центр окружности и любую точку на самой окружности. Длину радиуса обозначают буковй R.

Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Длину диаметра обозначают буквой d, диаметр равен двум радиусам d = 2R.

Число π (Пи) — это отношение длины окружности к длине ее диаметра: π = Cd = C2R
Число Пи является иррациональным числом, которое выражается бесконечной непериодической дробью:π = 3.1415926535898… Обычно используют округление числа Пи до 3.14

Длина окружности (периметр круга) — это длина замкнутой плоской кривой, ограничивающей круг. Длину окружности обозначают буквой C и её можно выразить в виде произведения двух радиусов на π или произведения числа π на величину диаметра окружности: C = 2πR = πd

4 — Как сделать выпадающий список при помощи элемента ActiveX

Действуем аналогично предыдущему способу, но выбираем иконку чуть ниже — из раздела «Элементы ActiveX».

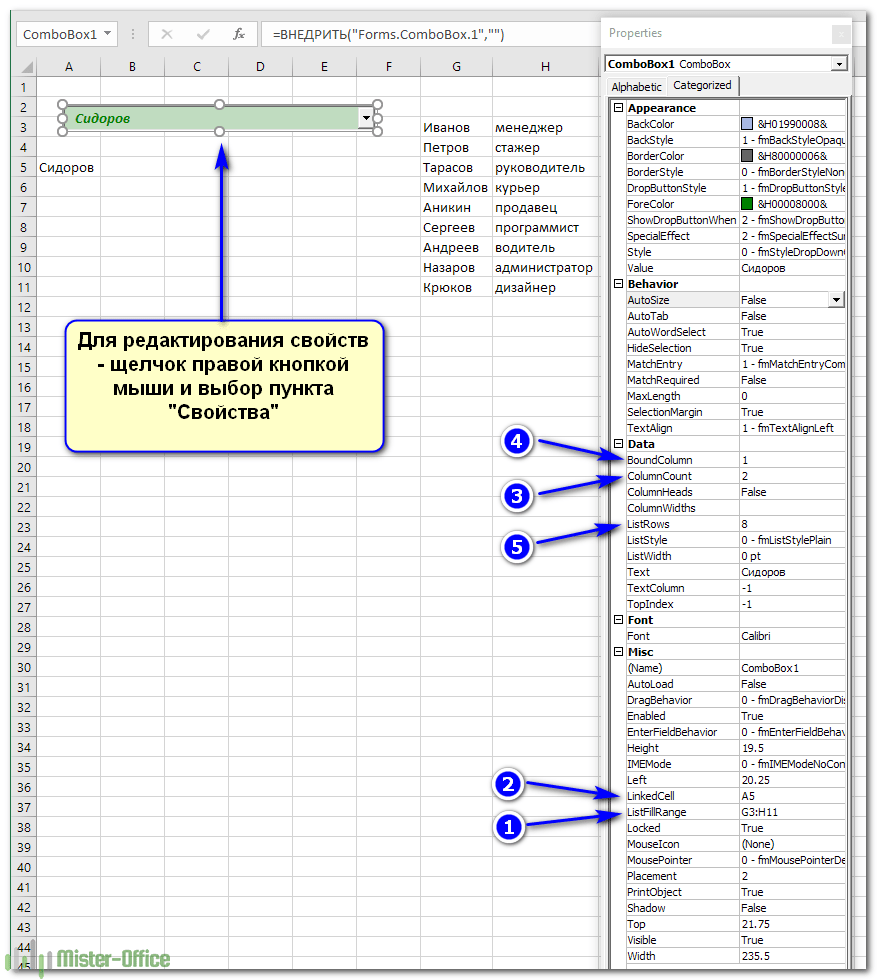
Определяем перечень допустимых значений (1)

Обратите внимание, что здесь для показа можно выбирать сразу несколько колонок. Затем выбираем адрес, по которому будет вставлена нужная позиция из перечня (2).Указываем количество столбцов, которые будут использованы как исходные данные (3), и номер столбца, из которого будет происходить выбор для вставки на лист (4)

Если укажете номер столбца 2, то в А5 будет вставлена не фамилия, а должность. Можно также указать количество строк, которое будет выведено в перечне. По умолчанию — 8. Остальные можно прокручивать мышкой (5).

Этот способ сложнее предыдущего, но зато возвращает сразу значение, а не его номер. Поэтому необходимость в промежуточной ячейке и обработке ее при помощи ИНДЕКС — отпадает. Думаю, таким выпадающим списком пользоваться гораздо удобнее.

Вариант 3. Выпадающий список на основе «умной» таблицы Excel.

Начиная с 2007 года таблица для Excel — уже не просто набор строк и столбцов. Если вы просто расположите показатели с привычном для нас табличном виде, то он не будет считать их таблицей. Существует специальное форматирование, после чего диапазон начинает вести себя как единое целое, приобретая целый ряд интересных свойств. В частности, он начинает сам отслеживать свои размеры, динамически изменяясь при корректировке данных.

Любой набор значений в таблице может быть таким образом преобразован. Например, A1:A8. Выделите их мышкой. Затем преобразуйте в таблицу, используя меню Главная — Форматировать как таблицу (Home — Format as Table). Укажите, что в первой строке у вас находится название столбца. Это будет «шапка» вашей таблицы. Внешний вид может быть любым: это не более чем внешнее оформление и ни на что больше оно не влияет.

Как уже было сказано выше, «умная» таблица хороша для нас тем, что динамически меняет свои размеры при добавлении в нее информации. Если в строку ниже нее вписать что-либо, то она тут же присоединит к себе её. Таким образом, новые значения можно просто дописывать. К примеру, впишите в A9 слово «кокос», и таблица тут же расширится до 9 строк.

Следовательно, автоматическое обновление набора используемой информации в списке можно организовать, если использовать содержимое какого-либо столбца «умной» таблицы.

Осталось только обозначить ее как источник. Проблема заключается в том, что программа в качестве источника в списке не понимает выражение вида

и не считает его формулой. Хотя в обычных выражениях на листе вашей рабочей книги это вполне будет работать. Эта конструкция обозначает ссылку на первый столбец. Но в поле «Источник» она почему-то игнорируется.

Чтобы использовать «умную таблицу» как источник значений для выпадающего списка, нам придется пойти на небольшую хитрость и воспользоваться функцией ДВССЫЛ (INDIRECT в английском варианте). Эта функция преобразует текстовую переменную в обычную ссылку.

Формула теперь будет выглядеть следующим образом:

Таблица5 — имя, автоматически присвоенное «умной таблице». У вас оно может быть другим. На вкладке меню Конструктор (Design) можно изменить стандартное имя на свое (но без пробелов!). По нему мы сможем потом адресоваться к нашей таблице на любом листе книги.

«Продукт» — название нашего первого и единственного столбца, присвоено по его заголовку.

Не забудьте также заключить все выражение в кавычки, чтобы обозначить его как текстовую переменную.

Теперь если в A9 вы допишете еще один фрукт (например, кокос), то он тут же автоматически появится и в нашем выпадающем списке. Аналогично будет, если мы что-то удалим. Задача автоматического увеличения выпадающего списка значений решена.

И еще один способ как сделать выпадающий список, в который будут автоматически добавляться новые значения, смотрите в этой статье: Создаем динамический выпадающий список в Excel при помощи формул.

Также рекомендую обратить внимание на это руководство: Как сделать выпадающий список с выбором нескольких значений. Надеемся, вы сможете теперь легко и быстро сделать выпадающий список в ячейке, чтобы с его помощью без ошибок вводить часто повторяющиеся данные в таблицу Excel

Надеемся, вы сможете теперь легко и быстро сделать выпадающий список в ячейке, чтобы с его помощью без ошибок вводить часто повторяющиеся данные в таблицу Excel.

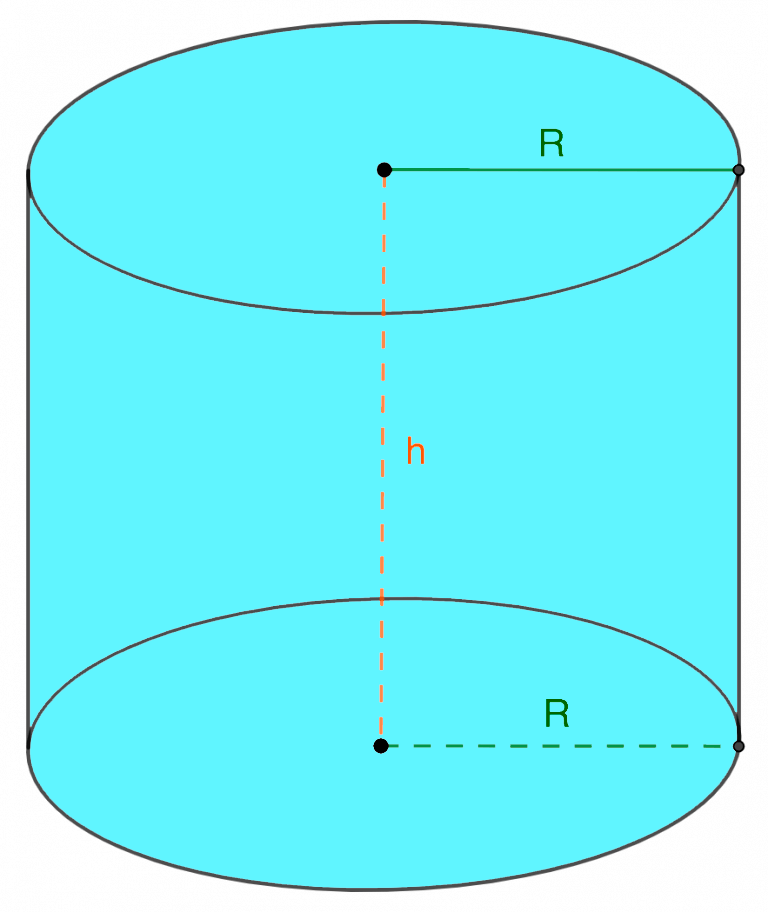
Цилиндр

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая  L.

Цилиндр называется прямым, если его образующие перпендикулярны основаниям.

Осевое сечение цилиндра  — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.

Основные понятия и свойства цилиндра:

1. Основания цилиндра равны и лежат в параллельных плоскостях.
2. Все образующие цилиндра параллельны и равны.
3. Радиусом цилиндра называется радиус его основания ($R$).
4. Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
5. Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
6. Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
7. Если высоту цилиндра увеличить в $m$ раз, то объем цилиндра увеличится в то же количество раз.
8. Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
9. Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.

Пример:

Сосуд в форме цилиндра заполнен водой до отметки $40$ см. Найдите, на какой высоте будет находиться уровень воды, если её перелить в другой сосуд в форме цилиндра, радиус основания которого в $2$ раза больше радиуса основания первого цилиндра. Ответ дайте в сантиметрах.

Решение:

Так как из сосудов перелили одинаковый объем жидкости, следовательно, при равных объемах отличаются радиусы и  высоты уровней жидкостей.

$V_1=V_2$;

$R_2=2R_1$, так как у второго цилиндра радиус в два раза больше радиуса первого.

$h_1=40;h_2-?$

Распишем объемы занимаемой жидкости в обоих сосудах и приравняем формулы друг к другу.

$V_1=πR_1^2·h_1=πR_1^2·40$;

$V_2=πR_2^2·h_2=π(2R_1)^2·h_2=4πR_1^2·h_2$.

$πR_1^2·40=4πR_1^2·h_2$

Получили уравнение, которое можно разделить на $πR_1^2$

$40=4 h_2$

Чтобы найти $h_2$ надо сорок разделить на четыре

$h_2=10$

Ответ: $10$

Площадь поверхности  и объем цилиндра

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

$S_{бок.пов.}=2πR·h$

Площадь поверхности цилиндра равна сумме  двух площадей оснований и площади боковой поверхности.

$S_{полн.пов.}=2πR^2+2πR·h=2πR(R+h)$

Объем цилиндра равен произведению площади основания на высоту.

$V= πR^2· h$

Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Составной цилиндр:

Чтобы найти объем составного цилиндра надо:

1. Разделить составной цилиндр на несколько цилиндров или частей цилиндра.
2. Найти объем каждого цилиндра.
3. Сложить объемы.

Сообщение об ошибке

При желании вы можете добавить какое-нибудь уведомление о допущенной ошибке при вводе данных в ячейку. Для это вам нужно выполнить несколько простых операций.

1. Повторите описанные выше шаги по вызову окна «Проверка вводимых значений».
2. Выберите какой-нибудь тип данных. В качестве примера мы укажем, что необходимо вводить «Действительное» число, которое больше 10.

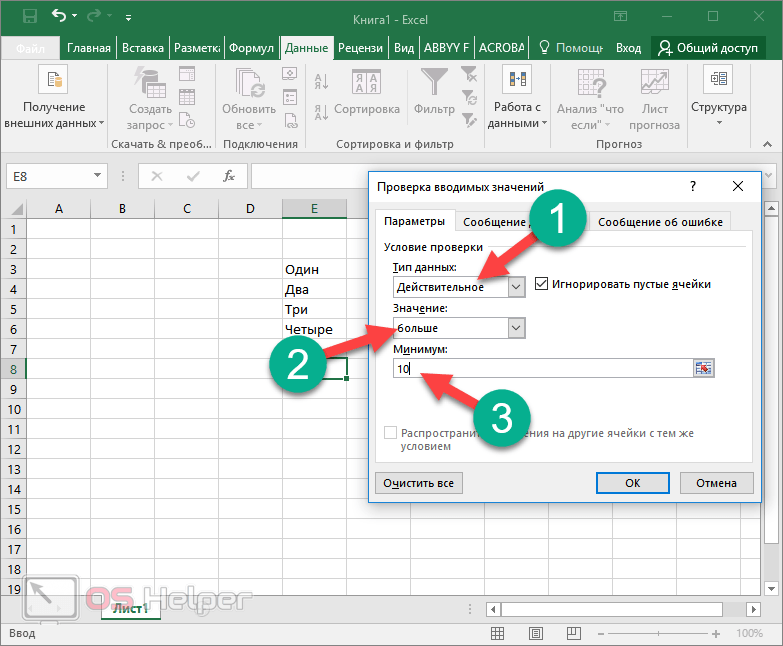
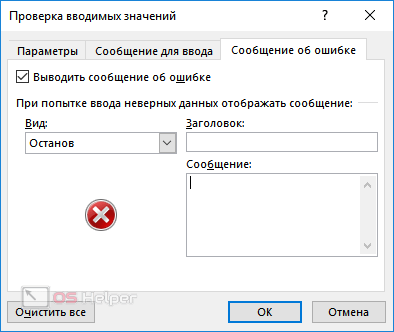
3. Теперь переходим на вкладку «Сообщение об ошибке».
4. Выбираем вид отображения:
   • «Останов»;
   • «Предупреждение»;
   • «Сообщение».
5. Указываем заголовок и текст уведомления.
6. Для сохранения проверки ввода значений нажмите на «OK»

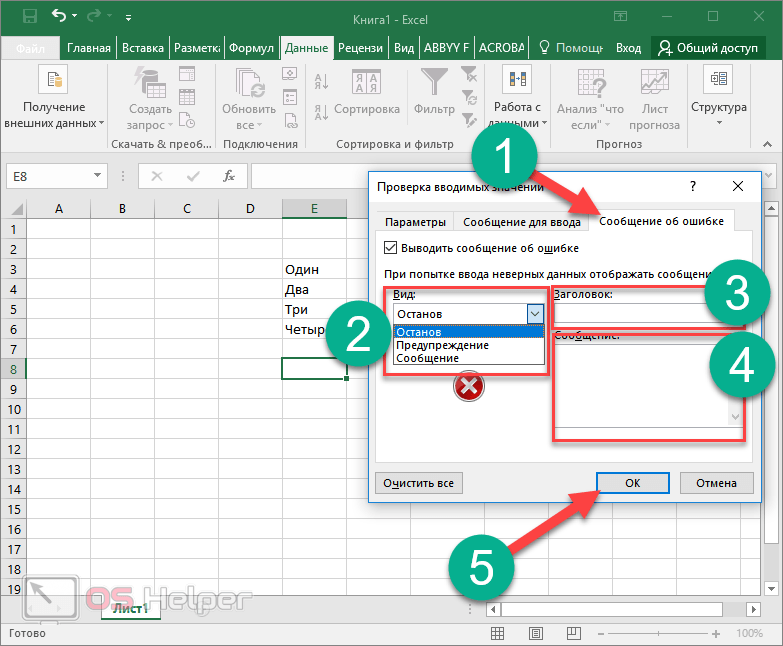
В качестве примера мы укажем следующие настройки.

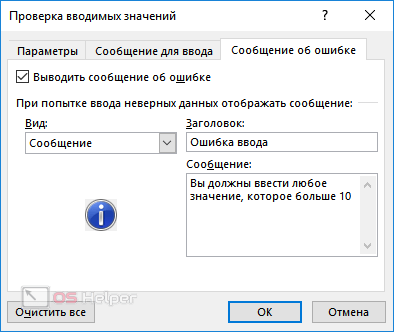
7. Введите любое число. Например, что-нибудь меньше указанного значения. Нажмите на клавишу Enter. И вы увидите уведомление о том, что была допущена ошибка ввода данных.

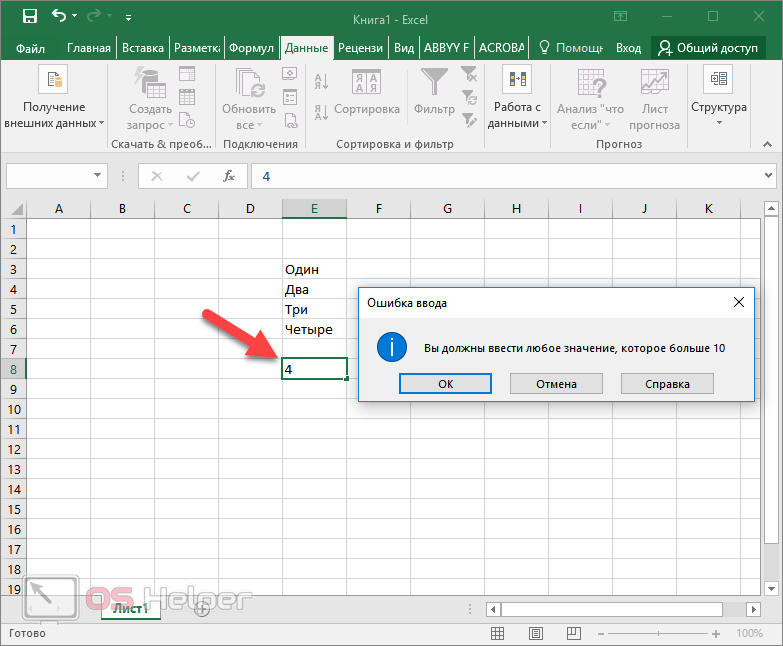
Если сделать тип «Останов», то ввести неверное значение не удастся.

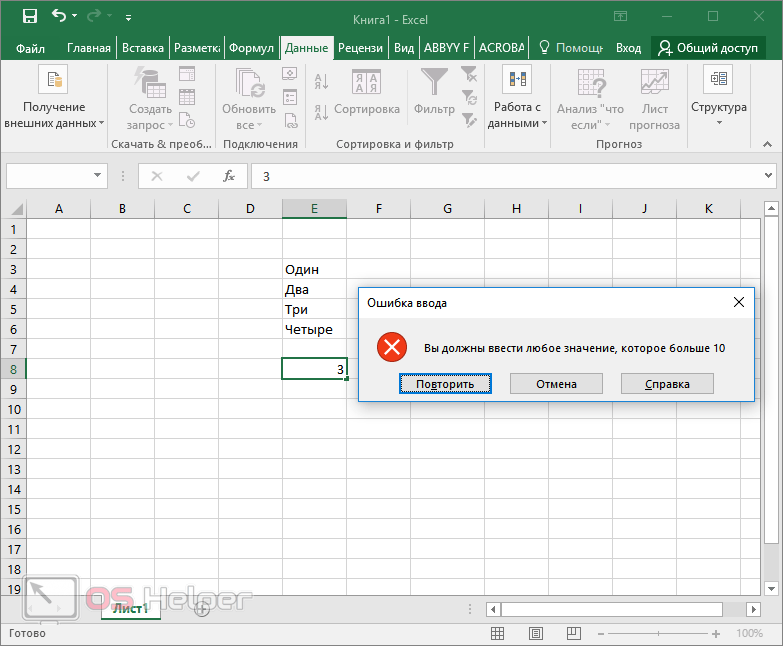
А теперь попробуйте убрать введенные настройки и оставить пустые поля.

В результате этого вы и увидите указанную ранее ошибку. То есть, если ничего не указывать вручную, редактор выведет предупреждение по умолчанию.

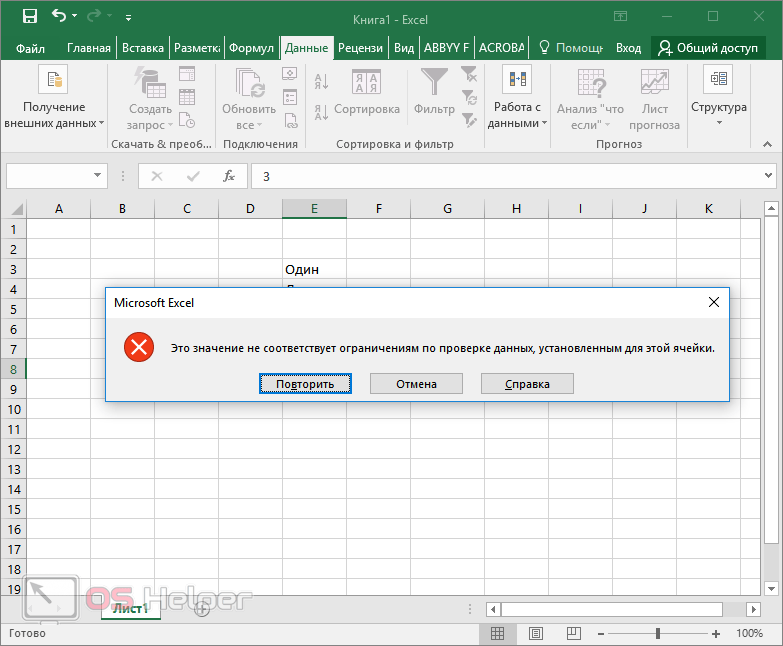
Отличие версий Microsoft Excel

Описанная выше инструкция подходит для современных редакторов 2010, 2013 и 2016 годов. По сравнению со старыми программами существуют некоторые отличия.

Откройте этот же файл в Экселе 2007. Введите неправильное значение. И вы увидите эту ошибку. То есть в современных редакторах текст сообщения по умолчанию был изменён. Привычный всем вид существовал до 2007 года.

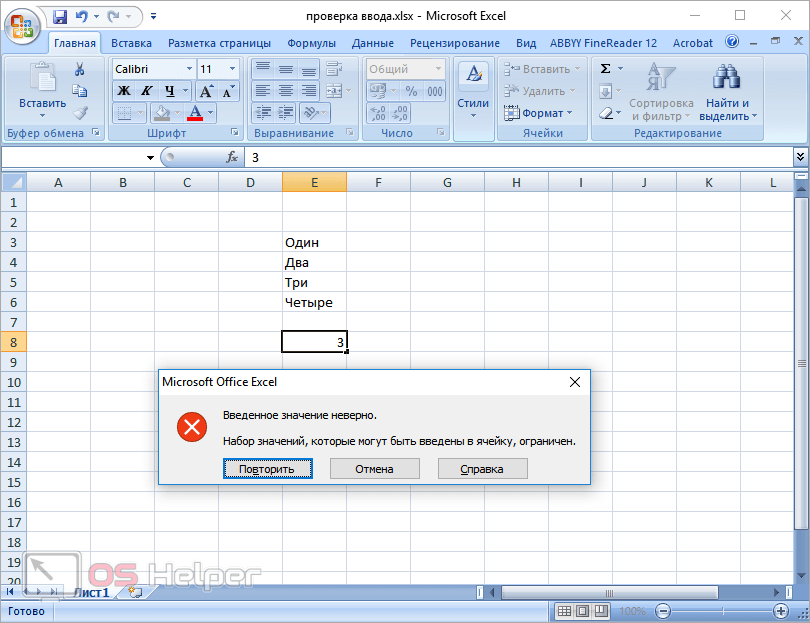
В старом Excel 2003 ошибка точно такая же.

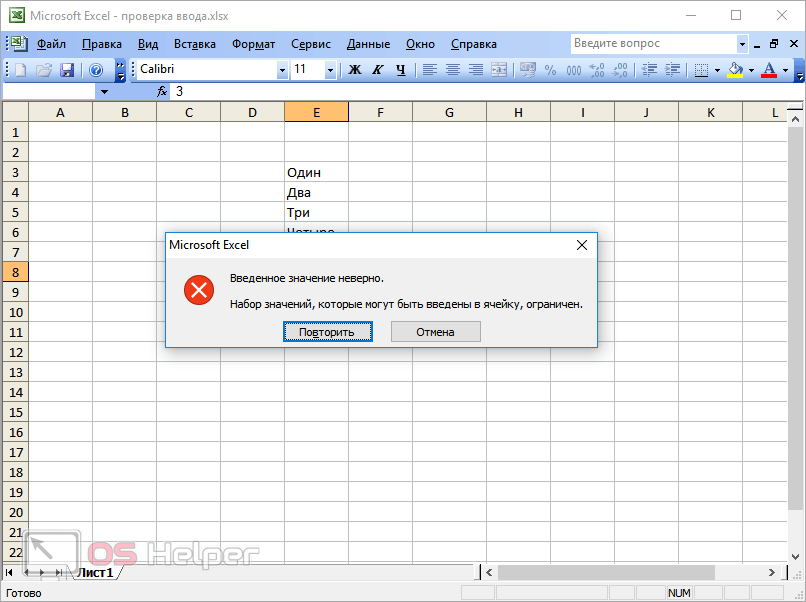
Вариант 1. Укажите заведомо большой источник значений для списка.

Самая простая и несложная хитрость. В начале действуем по обычному алгоритму действий: в меню выбираем на вкладке Данные – Проверка … (Data – Validation). Из перечня Тип данных (Allow) выберите вариант Список (List). Поставьте курсор в поле Источник (Source).  Зарезервируем в списке набор с большим запасом: например, до 55-й строки, хотя занято у нас только 7. Обязательно не забудьте поставить галочку в чекбоксе «Игнорировать пустые …». Тогда ваш «резерв» из пустых значений не будет вам мешать.

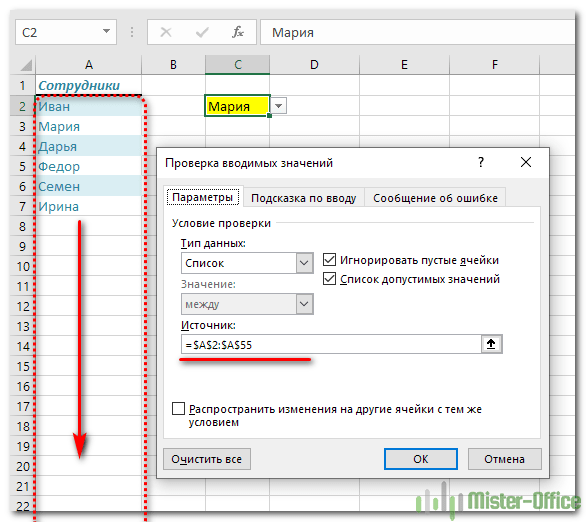
Действительно самый простой способ, но не слишком удобный. Ведь зарезервированное место может и закончиться…

Конечно, в качестве источника значений для выпадающего списка можно указать и весь столбец:

Но обработка такого большого количества ячеек может несколько замедлить вычисления. Особенно в больших таблицах Excel.

Что такое цилиндр

Разработка инженерных чертежей зданий, сооружений, оборудования начинается с самых простых фигур геометрии

Цилиндры применяют повсеместно, что объясняет важность умения рассчитывать их основные параметры, в том числе площадь. Цилиндром также называют классический головной убор

Цилиндрическую форму имеют трубы, архитектурные компоненты зданий, посуда, разнообразные резервуары.

Использование в производстве продукции именно такой формы позволяет значительно сократить затраты. К примеру, на изготовление сосуда в виде цилиндра уходит меньше материала, чем на выпуск аналогичных товаров в форме параллелепипеда. Это объясняется разницей в величинах площади боковой поверхности материального тела.

Цилиндрические предметы удобнее держать в руках и размещать в местах хранения. По этой причине бутыли с жидкостями разного состава, которые используют в медицине, салонах красоты и других сферах, имеют цилиндрическую форму. Многие химические вещества, в том числе, газы, агрессивные среды, нефтепродукты, масла, транспортируют в цистернах в виде цилиндров. Это связано с отсутствием уязвимых мест и максимальной герметичностью подобных резервуаров. В цилиндрической емкости центр тяжести находится ниже, чем в контейнере прямоугольной формы, что обеспечивает стабильность положения заполненного резервуара. Кроме того, давление на стенки цилиндра с жидкостью или газом распределяется более равномерно.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Цилиндром называют некое тело в геометрии, внутренние границы которого обозначены цилиндрической поверхностью и парой плоскостей, расположенных параллельно относительно друг друга и пересекающих эту поверхность.

Разберем основные понятия, с которыми часто сталкиваются школьники в процессе решения геометрических задач. К примеру, материальное тело обладает некой поверхностью

Величину площади этой поверхности важно знать для проведения вычислений в теории и на практике

Цилиндрическая поверхность представляет собой такую поверхность, которая сформирована с помощью параллельных прямых и некой кривой, называемой направляющей.

Цилиндр обладает основаниями, которые можно измерить. Они являются плоскими геометрическими фигурами. Для того чтобы получить основания, необходимо пересечь цилиндрическую поверхность парой плоскостей, расположенных параллельно по отношению друг к другу. Тот участок поверхности, который разделяет плоскости цилиндрических оснований, обозначают за боковую поверхность цилиндра. Плоскости оснований цилиндра высекают в своем перпендикуляре некий отрезок, называемый высотой цилиндра.

Существуют следующие виды цилиндров:

1. Прямой цилиндр с основаниями в виде кругов или эллипсов. В этом случае цилиндрическая ось расположена между центральными точками симметрии и является перпендикуляром к основаниям.
2. Косой цилиндр отличается от прямого геометрического тела расположением оси, то есть данный отрезок не перпендикулярен цилиндрическим основаниям.
3. Круговой цилиндр имеет направляющую в виде окружности.
4. Прямой круговой цилиндр (цилиндр вращения) получают в результате вращательного движения прямоугольника относительно какой-то стороны.
5. Эллиптический, параболический, гиперболический цилиндры названы так по форме основания, которые имеют вид эллипсов, парабол, гипербол соответственно. В случае параболического и гиперболического цилиндров объем измеряется бесконечностью.
6. Призма представляет собой цилиндр с основанием, которое обладает формой многоугольника.
7. Равносторонний цилиндр является таким цилиндром вращения, в котором наблюдается равенство диаметра основания и цилиндрической высоты.

Примечание 1

При параллельном расположении плоскостей основания и направляющей цилиндра форма границы данного основания идентична направляющей кривой.

Настраиваемые поля и суммарные задачи

Определить, как данные настраиваемого поля будут отображаться для суммарных задач, можно в диалоговом окне настройки полей, в разделе Calculation for task and group summary rows (Расчет для суммарных строк задач и групп), выбрав необходимое поле в списке (рис. 13.22, файл 16.mрр).

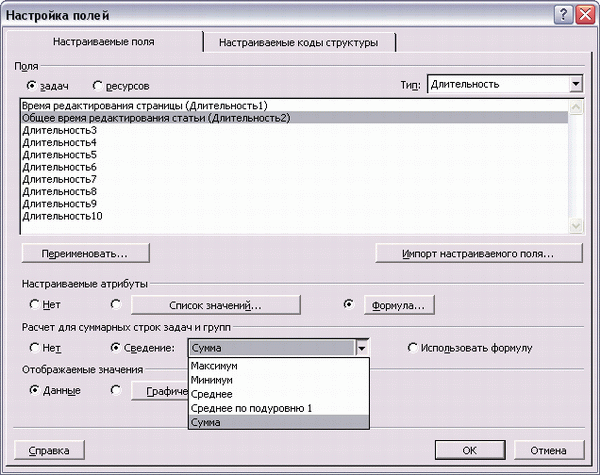
Рис. 13.22. Настройка расчетов для суммарных задач. Содержимое раскрывающегося списка зависит от типа выбранного поля

Раздел содержит три переключателя: None (Нет), Rollup (Сведение) и Use formula (Использовать формулу). Если выбрать первый, то данные настраиваемого поля будут рассчитываться только для обычных задач, а не для суммарных. Второй переключатель позволяет рассчитывать значение настраиваемого поля для суммарных задач, используя одну из операций, представленных в раскрывающемся списке. Состав этого списка меняется в зависимости от типов полей (табл. 13.2), кроме того, нельзя сводить данные для текстовых полей.

Название операции	Типы настраиваемых полей	Описание
And (И)	Flag (Флаг)	Логическое И. Если все вложенные строки в этом поле имеют значение Да, то результат операции — тоже Да. Если хотя бы одна из строк в этом поле содержит значение Нет, то и результатом логической операции будет Нет
OR (ИЛИ)	Flag (Флаг)	Логическое ИЛИ. Если хотя бы один из рядов содержит значение Да в этом поле, то операция сведения тоже даст Да
Average (Среднее)	Cost (Затраты), Duration (Длительность), Number (Число)	Сведение будет средним по всем значениям вложенных несуммарных рядов
Average First Sublevel (Среднее первого подуровня)	Cost (Затраты), Duration (Длительность), Number (Число)	Сведение будет средним по всем значениям вложенных несуммарных рядов и по всем значениям вложенных суммарных рядов первого уровня
Count All (Сложить все)	Number (Число)	При сведении будут складываться все суммарные и несуммарные ряды
Count First Sublevel (Сложить первый подуровень)	Number (Число)	При сведении будут складываться суммарные ряды первого уровня и все вложенные несуммарные ряды
Count Nonsummaries (Сложить несуммарные)	Number (Число)	При сведении будут сложены все несуммарные задачи
Maximum (Максимум)	Cost (Затраты), Duration (Длительность), Number (Число), Start (Начало), Finish (Окончание)	Результатом сведения будет максимальное значение среди всех значений ниже
Minimum (Минимум)	Cost (Затраты), Duration (Длительность), Number (Число), Start (Начало), Finish (Окончание)	Результатом сведения будет минимальное значение среди всех значений ниже
Sum (Сумма)	Cost (Затраты), Duration (Длительность), Number (Число)	Результатом сведения будет сумма всех значений ниже

Таблица 13.2. Операции для сведения данных в суммарных задачах

Если для расчета настраиваемого поля используется формула, то становится доступен третий переключатель — Use formula (Использовать формулу). Если выбрать его, то для расчета значений настраиваемого поля для суммарных задач будет использоваться та же формула, что и для обычных задач. В нашем случае (файл 16.mрр) удобнее использовать операцию сложения значений настраиваемого поля для задач, чем формулу. Ведь наша формула использует при расчете значения других полей, а значит, для них тоже нужно настроить параметры определения значения для суммарных задач. Если же этого не cделать, то значения этих полей для суммарных задач всегда будут нулевыми и результат нашей формулы тоже будет нулем.

На рис. 13.23 представлена таблица из файла 16.mрр с расчетами общей длительности редактирования статей после того, как мы настроили суммирование значений для фаз у поля Общее время редактирования статьи. Теперь значения в нем суммируются, а в остальных настраиваемых полях — по-прежнему нет.

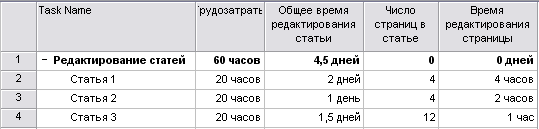
Рис. 13.23. Теперь общее время редактирования статей суммируется

Подсчитанная нами длительность фактически является трудозатратами на выполнение работы по редактированию. Однако эти данные нельзя автоматически внести в план проекта, то есть в поле Work (Трудозатраты) соответствующих задач, поскольку это поле не является настраиваемым и в него нельзя вводить формулы. Поэтому поместить полученные нами данные в это поле можно только вручную.

Модель, при которой данные рассчитываются в одном поле автоматически при изменении других полей, а потом должны быть вручную перенесены в план проекта, таит в себе одну опасность: можно случайно забыть ввести данные о трудозатратах в план проекта. В таком случае плановые трудозатраты задачи будут неверными, а значит, и план проекта в целом будет неточным. Чтобы трудозатраты задачи всегда соответствовали данным в настраиваемом поле Общее время редактирования статьи, воспользуемся индикаторами.

Формулы вычисления радиуса цилиндра

1. Через объем и высоту

Радиус цилиндра рассчитывается по формуле:

V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.

V = π R 2 h

• R – радиус основания цилиндра, т.е. окружности;
• π – число, округленное значение которого равняется 3,14.

2. Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

S_бок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:

S = 2 π Rh

3. Через полную площадь поверхности

Радиус цилиндра равен:

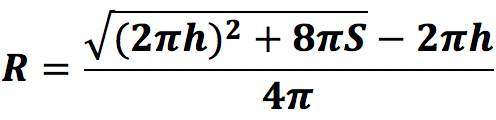
Данная формула получена следующим образом:

S – полная площадь поверхности фигуры, равная:

S = 2 π Rh + 2 π R 2 или S = 2 π R(h + R)

Возьмем первое выражение. Если перенести S в правую часть, получим:

2 π R 2 + 2 π Rh – S = 0

Можно заметить, что это квадратное уравнение вида ax 2 + bx + c = 0, где:

R является корнем данного уравнения (x). Подставив в стандартную формулу для расчета корней наши значения a, b и с получаем*:

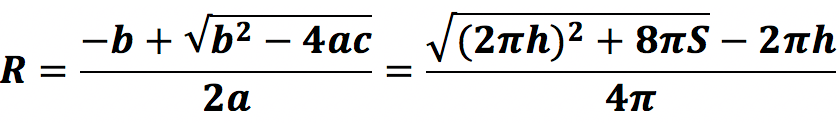
* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.

Свойства

Через диаметр цилиндра можно рассчитать его радиус и периметр основания цилиндра. Радиус будет равен половине диаметра, а периметр – его произведению на число π. r=D/2 P=πD

Зная диаметр и высоту цилиндра, можно узнать площадь, объем, диагональ цилиндра и остальные параметры. Площадь боковой поверхности цилиндра представляет собой площадь прямоугольника, сторонами которого являются периметр основания цилиндра и его высота. Чтобы затем найти площадь полной поверхности цилиндра через диаметр и высоту, нужно к площади боковой поверхности добавить площадь верхнего и нижнего оснований, каждое из которых равно произведению числа π на четверть квадрата диаметра. S_(б.п.)=hP=πDh S_(п.п.)=S_(б.п.)+2S_(осн.)=πDh+(πD^2)/2=πD/2(2h+D) P=πD

Объем цилиндра представляет собой площадь его основания, умноженную на высоту. Чтобы найти объем цилиндра через диаметр и высоту, нужно умножить квадрат диаметра на четверть числа π и на высоту. V=(πD^2 h)/4 P=πD

Диагональ цилиндра находится из прямоугольного треугольника, в котором она является гипотенузой, а катеты представлены высотой и диаметром цилиндра. По теореме Пифагора диагональ цилиндра через высоту и диаметр цилиндра равна квадратному корню из суммы их квадратов. (рис. 25.1) d=√(h^2+D^2 ) P=πD

Чтобы найти радиус сферы вписанной в цилиндр, если его диаметр равен высоте, нужно разделить диаметр цилиндра либо высоту на два, так как радиус вписанной сферы равен радиусу цилиндра. (рис.25.2) r_1=h/2=D/2 P=πD

Радиус сферы, описанной вокруг цилиндра, при соблюдении тех же условий (равенство диаметра цилиндра и его высоты) равен половине диагонали цилиндра.(рис.25.3) R=d/2=√(h^2+D^2 )/2

Заполнение данными

Заполнять настраиваемые поля можно двумя способами. Первый, традиционный для предыдущих версий MS Project, — добавить поле в таблицу и редактировать данные в нем так же, как и в остальных полях. Второй способ, которым можно редактировать значения настраиваемых полей, появившийся только в MS Project 2002, — использовать вкладку Custom Fields (Настраиваемые поля) в диалоговом окне сведений о задаче или ресурсе.

На этой вкладке представлены все существующие в проекте настраиваемые поля, относящиеся к задачам (а на аналогичной вкладке в диалоговом окне сведений о ресурсе будут расположены поля, относящиеся к ресурсам). Таблица в центре диалогового окна состоит из двух колонок. В левой колонке, Custom Field Name (Название настраиваемого поля), указано название поля, а и правой, Value (Значение), — его значение для текущей задачи. Например, на рис. 13.17 (файл IS.mpp) мы редактируем значение поля Результат для задачи Сбор предложений от авторов. Результатом выполнения задачи будет Файл предложений в редакционном формате.

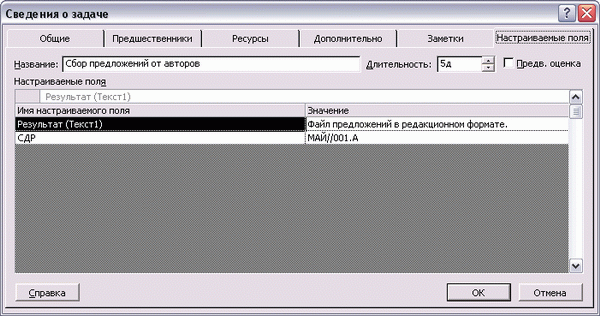
Рис. 13.17. Заполнение значения настраиваемого поля для задачи

ПРИМЕЧАНИЕ

Для того чтобы MS Project «понял», что вы хотите использовать настраиваемое поле, и отобразил его в диалоговом окне, нужно предварительно переименовать это поле.

Как вы могли заметить на рис. 13.17, поле WBS (СДР) тоже находится в списке настраиваемых. Это произошло потому, что мы изменили его настройки. Если же не настраивать структуру кодов задач, то это поле не будет числиться в списке настраиваемых.

Примеры расчета площади поверхности цилиндра

Для понимания приведенных формул, попробуем посчитать площадь поверхности цилиндра на примерах.

1. Радиус ос­но­ва­ния цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.

Площадь боковой поверхности рассчитывается по формуле: S_бок. = 2πrh

S_бок. = 2 * 3,14 * 2 * 3

S_бок. = 6,28 * 6

S_бок. = 37,68

Площадь боковой поверхности цилиндра равна 37,68.

2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?

Площадь полной поверхности рассчитывается по формуле: S = 2πr2 + 2πrh

S = 2 * 3,14 * 62 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

S = 226,08 + 150,72

S = 376,8

Площадь поверхности цилиндра равна 376,8.

3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.

Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:

h = Sбок./2πr

Значение радиуса получаем из формулы: d = 2r

h = 24π / (2π * 0,5d)

h = 24π / (2π * 0,5 * 3)

h = 12 / 1,5

h = 8

Высота цилиндра равна 8.

Заключение

Цилиндр, как геометрическая фигура, играет важную роль в различных областях нашей жизни. Понимание того, как рассчитать его объем, является ключевым навыком во многих профессиональных и академических областях. Этот расчет не только улучшает наше понимание геометрии, но и обеспечивает практическую пользу в инженерии, строительстве, промышленности и многих других сферах. Таким образом, знание и умение применять математические формулы для расчета объема цилиндра открывает двери для решения сложных практических задач и способствует развитию технологических и научных инноваций.

Последние вычисления