Цилиндры

Развертка

Как уже было упомянуто выше, всего существует две площади поверхности цилиндра: боковой поверхности и полной поверхности. У каждой из них также есть и своя развертка. Разберемся, как они выглядят.

Развертка боковой поверхности

Легче всего представить себе развертку боковой поверхности цилиндра, посмотрев на этикетку пластиковой бутылки. Когда вы ее отклеиваете, то видите прямоугольник. То же самое и с цилиндрическим геометрическим телом: развёрткой его боковой поверхности является прямоугольник. Его длина соответствует длине окружности, лежащей в основании, а ширина — высоте самой трехмерной фигуры.

Развертка полной поверхности

Если развернуть полную поверхность цилиндра, получится примерно то же самое, только с двумя дополнительными элементами в виде окружностей оснований. Выглядит это так:

Основные определения и свойства цилиндра

      Рассмотрим две   α   и   β   и произвольную   лежащую в плоскости   α   (рис. 1).

Рис.1

      Если из каждой точки окружности опустить   β,   то основания этих перпендикуляров образуют на плоскости   β   окружность радиуса   r,   центр   O₁   которой является основанием перпендикуляра, опущенного из точки   O   на плоскость   β   (рис.2).

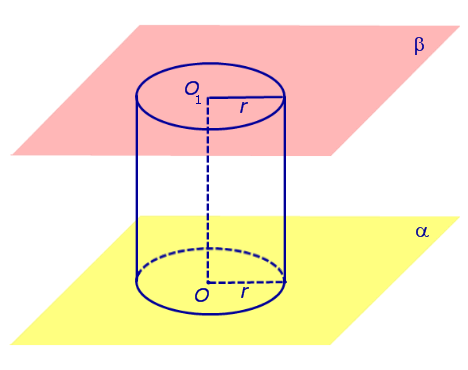
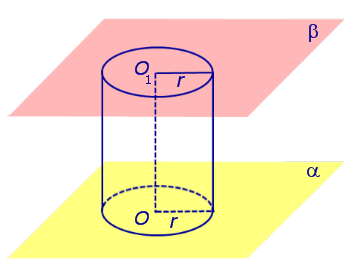
Рис.2

      Определение 1.

	Отрезок , опущенного из любой точки окружности с центром   O   на плоскость  β ,   который заключен между плоскостями   α   и   β ,   называют образующей цилиндра.
	Совокупность всех образующих цилиндра называют цилиндрической поверхностью.
	Фигуру, ограниченную цилиндрической поверхностью и плоскостями   α   и   β,   называют цилиндром.
	Отрезок   OO1   называют осью цилиндра .
	на плоскости   α   с центром в точке   O   называют радиусом цилиндра.
	α   и   β ,   называют высотой цилиндра.
	Круги с центрами   O   и   O1   на плоскостях   α   и   β ,   называют основаниями цилиндра.

      Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра. Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра.

      Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

     Замечание 3. Прямая   OO₁   является цилиндра, а середина отрезка   OO₁   является цилиндра.

Как найти высоту цилиндра

Рассмотрим варианты нахождения высоты фигуры, а также длины ее образующей (которая равна этой высоте).

Первым делом взглянем на формулу: \(V=\pi R^2\times H\), где V — объем цилиндра, R — радиус основания, H — высота фигуры.

Через эту формулу можем выразить высоту:

\(H=\frac V{\pi R^2}\)

Таким образом мы можем узнать H данного геометрического тела, если нам известен его объем и радиус. Если же вместо радиуса мы знаем диаметр, формула расчета будет выглядеть так:

\(H=\frac{4V}{D^2}\)

В случае, когда нам известен диаметр и площадь фигуры, мы так же можем найти высоту

Следует обратить внимание, что в зависимости от того, будет ли известна площадь боковой или полной поверхности, формула будет меняться

Для расчета S боковой поверхности (часть, ограниченная цилиндрической поверхностью) цилиндра мы используем формулу:

\(S=2\pi RH\)

выражаем H и получаем:

\(H=\frac S{2\pi R}\)

Если известна S полной поверхности (включает в себя площадь оснований фигуры), используем формулу:

\(S=2\pi R(H+R)=2\pi R\times H+2\pi R^2\)

выражаем H и получаем:

\(H=\frac{S-2\pi R^2}{2\pi R}\)

Для третьего способа нужно будет провести прямоугольное сечение, ширина которого должна будет совпадать с диаметрами оснований, а длина — с образующими цилиндра.

Таким образом, получается прямоугольный треугольник САВ. А так как высота равна образующей, мы можем вычислить ее по теореме Пифагора:

\(СВ^2=АС^2-АВ^2\)

\(H=СВ=\sqrt{АС^2-АВ^2}\)

Объем цилиндра. Площадь боковой поверхности цилиндра.Площадь полной поверхности цилиндра

      Для цилиндра с   r   и   h   (рис. 5)

Рис.5

введем следующие обозначения

V	объем цилиндра
Sбок	площадь
Sполн	площадь
Sосн	площадь

      Тогда справедливы следующие формулы для вычисления объема, площади :

S_осн = πr2,

V = S_оснh = πr2h,

S_бок= 2πrh,

S_полн = 2πr2 + 2πrh == 2π(r + h).

      Замечание 7. Формула объема цилиндра   V = πr2h   может быть получена из

при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Виды цилиндров

1. Прямой цилиндр – имеет одинаковые симметричные основания (круг или эллипс), параллельные друг другу. Отрезок между точками симметрии оснований перпендикулярен им, является осью симметрии и высотой фигуры.
2. Наклонный цилиндр – имеет одинаковые симметричные и параллельные друг другу основания. Но отрезок между точками симметрии не перпендикулярен этим основаниям.
3. Косой (скошенный) цилиндр – основания фигуры не взаимно параллельны.
4. Круговой цилиндр – основаниями является круг. Также выделяют эллиптические, параболические и гиперболические цилиндры.
5. Равносторонний цилиндр – прямой круговой цилиндр, диаметр основания которого равен его высоте.

Сами прямые называют образующими цилиндрической поверхности.
Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.

Так как все образующие и ось перпендикулярны плоскости альфа, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).

Если построить ещё одну плоскость бета, которая будет параллельна плоскости альфа, то отрезки образующих, заключённые между плоскостями альфа и бета будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости бета, дают окружность, равную окружности, лежащей в плоскости альфа.

Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях альфа и бета) называется цилиндром.
Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.

Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.

Сечения цилиндра различными плоскостями

Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого – образующие, а две другие – отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).

Основные формулы

Формула для вычисления площади боковой поверхности цилиндра: Sбок=2пRL.

То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: Sполн=2пR(R+L).

Примеры и разбор решения заданий тренировочного модуля

Дан цилиндр.

Выберите значение площади его боковой поверхности

1. 60π
2. 192π
3. 120π
4. 36π

Решение:

Площадь боковой поверхности вычисляется по формуле: S=2πRL.

R=6, L=10

Подставим: S=2π·6·10=120π.

Ответ: 3) 120π

Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.

Решение:

Sполн=2πR(R+L)

По условию задачи L=R+6.

144π=2πR(R+R+6).

Получили квадратное уравнение относительно радиуса:

R2+6R-72=0

R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.

Ответ: 12.

Задача

Осевое сечение цилиндра – квадрат со стороной 20 см. Найти высоту цилиндра, радиус цилиндра, ось цилиндра и площадь основания цилиндра.

Решение

Одна из сторон осевого сечения – образующая (она же равна оси цилиндра и она же равна высоте). Значит, высота и ось равны 20 см. Далее, вторая сторона осевого сечения – диаметр основания. Он равен 20 см, значит, радиус – 10 см. Наконец, площадь основания ищется по формуле

Итак, ребята, на этом уроке мы изучили, что такое цилиндрическая поверхность, её образующая; цилиндр, все его элементы и сечения; площади поверхностей цилиндра.

Находим недостающие проекции точек на комплексных чертежах цилиндра и конуса

Ассоциативные чертежи в «Инженерной графике» называют комплексными.

Как найти недостающие проекции точек на комплексном чертеже цилиндра?

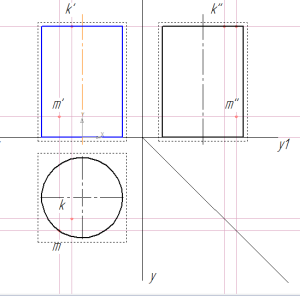
находим недостающие проекции точки m цилиндре

Построение недостающих проекций точек на цилиндре аналогично нахождению их на призме. Принцип тот же, только вместо граней, здесь окружность.  Для нашего цилиндра недостающие проекции точек К и М находятся, как показано на рисунке при помощи вертикальных и горизонтальных линий связи.

Подробнее о процессе построения смотрите на уроке как найти проекции точек на пирамиде и призме

Как найти недостающие проекции точек на комплексном чертеже конуса?

находим проекции точек на конусе

Необходимо построить недостающие проекции точек К и М на комплексном чертеже конуса.

Точка М задана фронтальной проекцией m’, точка К – горизонтальной проекцией k.

построения при нахождении горизонтальной проекции точки

Построим горизонтальную проекцию m. Для этого:

1. через точку m’ и вершину конуса s проводим вспомогательную прямую до пересечения ее с основанием в точке a.
2. Затем через полученную точку а проводим вертикальную  линию связи до пересечения с окружностью основания конуса в точке b.
3. Через полученную точку b и вершину конуса s проводим прямую.
4. Опускаем вертикальную линию связи из точки m’ до пересечения с прямой bs.
5. Горизонтальная проекция m найдена.

Профильная проекция m’’ находится обычным образом по линиям связи.

Фронтальная проекция (k’) находится таким же, вышеописанным образом. Вот рисунок

строим фронтальную проекцию точки k

Профильную проекцию (k’’) находим по линиям связи.

Окончательно комплексные чертежи цилиндра и конуса выглядят так.

готовый комплексный чертеж конуса

готовый комплексный чертеж цилиндра

Для лучшего понимания материала рекомендую посмотреть видеоурок.

Определение цилиндра как геометрической фигуры

Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».

Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны

Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.

Площадь поверхности цилиндра

Площадь боковой поверхности

К вычислению площади боковой поверхности цилиндра

Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.

Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой \displaystyle{ h } и длиной \displaystyle{ P }, равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:

\displaystyle{ S_b = P h }

В частности, для прямого кругового цилиндра:

\displaystyle{ P = 2 \pi R }, и \displaystyle{ S_b = 2 \pi R h }, здесь и далее \displaystyle{ R } — радиус основания цилиндра.

Для наклонного цилиндра площадь боковой поверхности равна длине образующей, умноженной на периметр сечения, перпендикулярного образующей:

\displaystyle{ S_b = P_{\perp} h }

Простой формулы, выражающей площадь боковой поверхности косого цилиндра через параметры основания и высоту, в отличие от объёма не существует. Для наклонного кругового цилиндра можно воспользоваться , а затем умножить полученное значение на длину образующей.

Площадь полной поверхности

Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.

Для прямого кругового цилиндра:
\displaystyle{ S_{p} = 2 \pi R h +2 \pi R^2 = 2\pi R (h+R) }

Виды цилиндров

Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.

Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.

По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.