Измерить – значит, сравнить
На помощь человеку приходят числа, используя которые можно было сравнить предметы по величине. Так в одном известном мультфильме длину удава измеряли в «попугаях», сравнивая величину удава с длиной попугая.
 Из мультфильма «38 попугаев».
Из мультфильма «38 попугаев».
Длина удава 38 «попугаев». Понятно, что удав в 38 раз длиннее попугая. Но попугаи бывают разными. Если взять другого попугая, тот же удав будет, например, 45 «попугаев». Что делать?
Нужно найти тело, принимаемое за единицу измерения, с которой сравниваются другие тела.
В практической деятельности человеку приходится часто измерять длину, массу и время. В разных странах вводились разные единицы измерения этих величин. Существовали такие единицы, как «лошадиная сила», локоть, бочка. Но ведь и локоть, и бочка могут быть разными, поэтому о точности выполнения работы говорилось приблизительно.
 (Источник)
(Источник)
Сравнивать нужно только однородные физические величины. Длину тела нужно сравнивать с длиной другого тела, а массу тела – только с массой другого тела, принятого за единицу измерения. Так массу удава из мультфильма можно было сравнить с массой обезьянки. Удав имеет массу 195 «обезьянок». Что бы это значило?
Выход был найден, когда ввели систему единиц СИ. Чтобы измерить любую величину, нужно сравнить ее с однородной величиной, принятой за единицу. Как же выбирают эти единицы?
Наиболее распространено измерение длины, размеров пройденного пути, расстояния. Все эти величины измеряются в метрах. Один метр получили следующим образом. Взяли одну сорока миллионную часть меридиана, который проходит через столицу Франции – Париж. Длину этой части и приняли за 1 метр. На стержне, изготовленном из иридия и платины, нанесли два деления, расстояние между которыми равно одному метру. Такой сплав меньше всего подвержен температурному влиянию, которое может изменить длину тела. Это стержень и есть эталон длины, с которым сравнивают единицу длины во многих странах мира. Метровые линейки – это многочисленные копии эталона, которыми как раз и можно пользоваться.
Эталон длины
 (Источник)
(Источник)
Первый эталон метра был изготовлен из латуни в 1795 г. С 1960 г. используется изготовленный с помощью электронных технологий эталон из сплава иридия и платины.
Существует и эталон массы, равный одному килограмму. Он также изготовлен из сплава иридия и платины.
 (Источник)
(Источник)
Эталоны длины и массы хранятся в г. Севр, вблизи Парижа, где располагается Международная палата мер и весов. В 1960 году метр начали сравнивать с величинами, относящимися к разделу «Световые явления». Подробности о свете изучаются в старших классах.
Со светом связана и единица времени – 1 секунда. А до 1960 года (год введения СИ) за основу подсчета времени брали время оборота Земли вокруг Солнца – 1 год, который по календарю состоит из 12 месяцев. Месяцы делятся на сутки – время полного оборота Земли вокруг своей оси, сутки — 24 часа, в каждом из которых 60 минут. А одна шестидесятая часть минуты и есть одна секунда.

Время «хранят» при помощи очень точных часов – устройств, предназначенных для измерения времени. Действие любых часов основано на повторяющихся процессах – колебаниях. Чем меньше период (время одного полного колебания), тем часы более точные.
При изучении быстро протекающих процессов требуется измерять миллиардные и еще более мелкие доли секунды. Для этого служат атомные часы.
 (Источник)
(Источник)
Ученик седьмого класса, конечно же, умеет измерять длину и время, массу продуктов определяют продавцы с помощью весов.
По мере изучения физики будет идти знакомство с различными физическими величинами, способами и приборами их измерения. А сейчас надо знать:
- чтобы измерить физическую величину, ее надо сравнить с однородной величиной, принятой за единицу;
- за основу физических величин берутся эталонные значения, то есть образец сравнения.
- для всех величин существуют свои способы, устройства и единицы измерения.
Как измерить длину. Погрешности измерений
На практике измерить длину отрезка достаточно просто:

- Приложить линейку к отрезку.
- Совместить ноль с началом отрезка.
- Определить число, соответствующее концу отрезка.
- Записать результат измерения.
В приведенном примере длина отрезка 9,9 см. Как точен этот результат? Он точен до 1 мм, так как на линейке нет меньших делений. Не надо путать значения слов «штрих» и «деление».
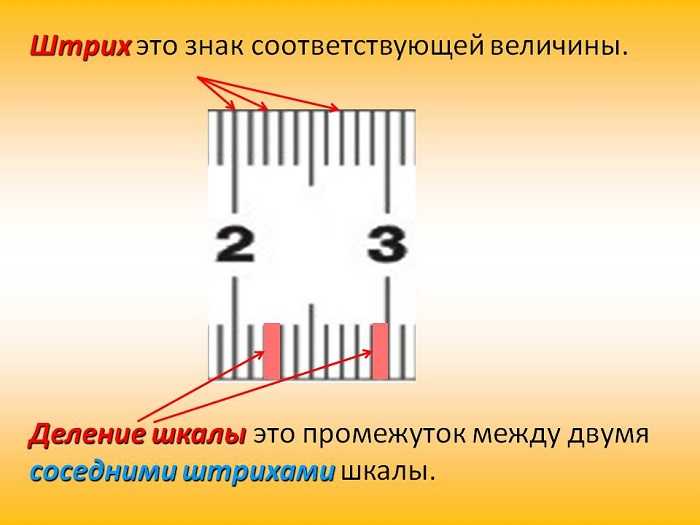 (Источник)
(Источник)
Численное значение самого маленького деления шкалы прибора называется ценой деления.
Чтобы определить цену деления прибора (например, линейки), нужно взять любые два рядом стоящие числа и их разность поделить на число делений между ними (т.е. промежутков между штрихами).
Цена деления линейки = (7 см – 6 см)/10 = 0,1 см = 1 мм.
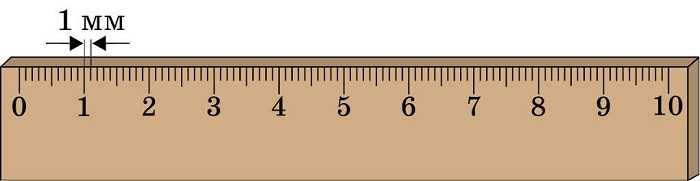
И чтобы начать измерение, прежде всего надо найти цену деления прибора, который используется в данном случае. Любое измерение дает некоторую погрешность, зависящую от качества прибора. Поэтому ее называют погрешностью прибора.
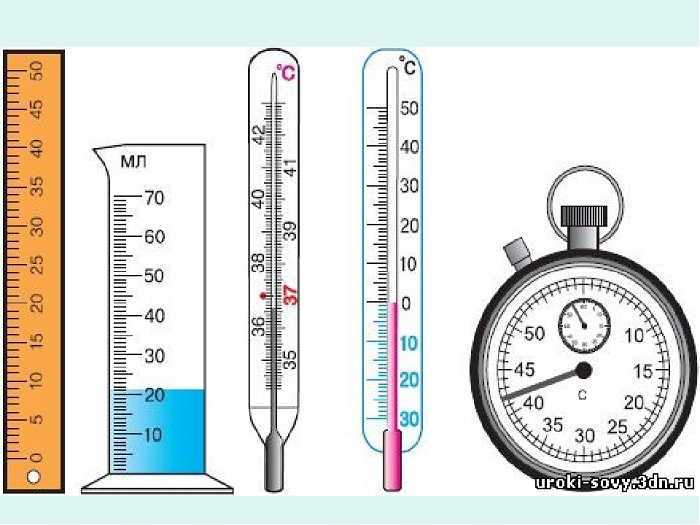 Шкалы различных приборов. (Источник)
Шкалы различных приборов. (Источник)
Известно, что измерить какую-то величину – это значит сравнить ее с эталоном. На практике пользуются не эталонами, а специальными приборами (линейка, часы и др.), которые являются копиями с эталонов, изготовленными с определенной точностью. Абсолютно точных измерений не бывает. При использовании линейки допускается погрешность отсчета, которая равна половине цены деления прибора (0,5 мм). Сумма погрешностей прибора и отсчета называется абсолютной погрешностью. Она равна цене деления прибора.
Абсолютная погрешность обозначается значком Δ (дельта). Для школьной линейки Δ = 1 мм. Δ показывает, на сколько совершается ошибка при использовании того или иного прибора. Для более точных измерений используется штангенциркуль. В устройстве штангенциркуля заложено две шкалы, неподвижная (Δ = 1 мм) и подвижная (Δ = 0,1 мм).
 Штангенциркуль. Микрометр.
Штангенциркуль. Микрометр.
А вот при помощи микрометра, где используется не перемещение шкалы, а ее вращение измерить длину можно с точностью до 0,01 мм. Но это еще не предел. В очень точных технологиях определяются размеры с точностью до 10-7м, в научных разработках точность возрастает во много раз. Но для этого нужны сверхточные приборы.
На практике, используя приборы, необходимо учитывать качество измерения. Величина, которая помогает это учесть, называется относительной погрешностью σ (сигма) и выражается в процентах.
σ = Δ / L ( L – измеренная величина)
Пример: Требуется замерить длину L отрезка различными приборами: 1) линейкой, 2) штангенциркулем и 3) микрометром. Длина отрезка получилась 55 мм. Какова относительная погрешность этих трех измерений?
1) Δ1 = 1 мм, L = 55 ± 1 мм, σ1 = 1 мм / 55 мм ≈ 0,018 (1,8%);
2) Δ2 = 0,1 мм, L = 55 ± 0,1 мм, σ2 = 0,1 мм / 55мм ≈ 0,0018 (0,18);
3) Δ3 = 0,01 мм, L = 55 ± 0,01 мм, σ3 = 0,01 мм / 55мм ≈ 0,00018 (0,018%).
Как видно, более точный прибор (микрометр) дает меньший процент ошибки.
Для каждого конкретного измерения в технике, практической деятельности человека и в науке существует своя точность измерения, в соответствии с которой применяются измерительные приборы.
Измерение объема. Мензурка
При измерении пространства нужно перейти к трем измерениям, так как представление о пространстве дает объем. Известны формулы объемов параллелепипеда, куба, шара, цилиндра.
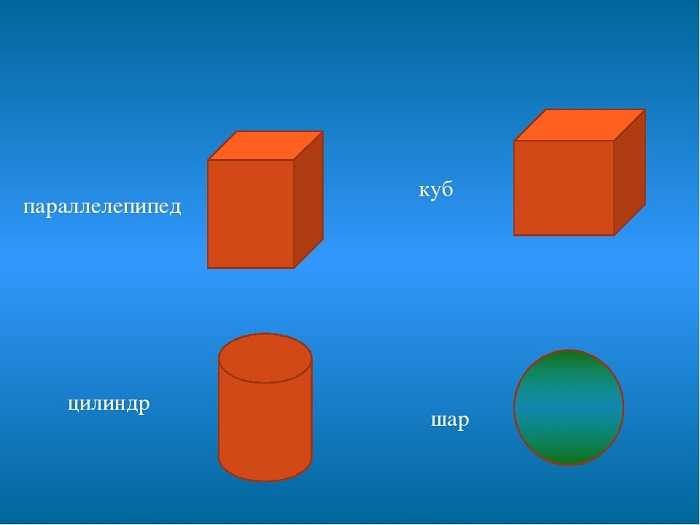 (Источник)
(Источник)
Объем любого тела измеряется в кубических метрах (есть кратные и дольные единицы). Из математики известны формулы объемов:
Vпар = а ∙ в ∙ с (произведение длины, ширины и высоты),
Vк = а3 (а — ребро куба),
Vцил = π ∙ r2 ∙ h (r — радиус основания, h – высота цилиндра),
Vш = 4/3 π ∙ R3 (R – радиус шара).
О вычислении объемов более сложной, но правильной, формы рассказывается в старших классах. А как определить объем, например, камня, форма которого может быть самой различной? Для измерения объемов таких тел используется специальный и очень простой прибор, который называется мензурка (или измерительный цилиндр). Это стеклянный сосуд с делениями. При помощи этого цилиндра легко найти объемы сыпучих тел и жидкостей. Для этого достаточно их засыпать вещество или налить в мензурку жидкость и, зная цену деления, определить объем.
 (Источник)
(Источник)
На мензурке обычно ставится единица измерения в миллилитрах. Литр – это широко применяемая единица объема, равная одной тысячной кубического метра. 1 мл = 1 см3 = 10-6 м3.
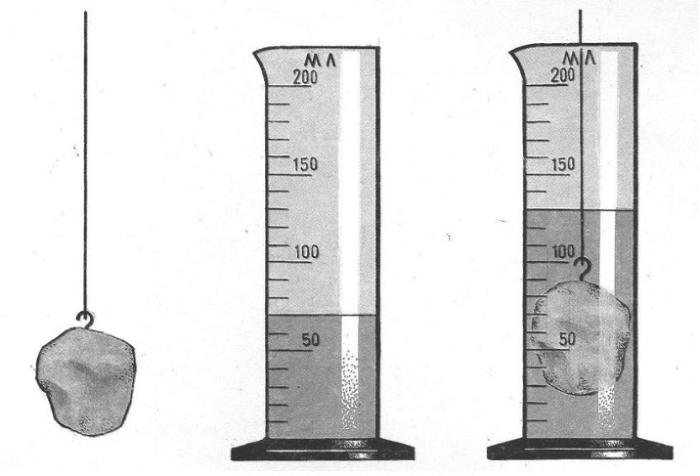
Определить объем камня или любого другого тела неправильной формы с помощью мензурки можно при условии, что тело имеет размеры, позволяющие опустить его в мензурку.
 (Источник)
(Источник)
Налить в мензурку воду и зафиксировать ее объем. Прикрепить тело неправильной формы к нити
Осторожно опустить полностью в воду. Уровень воды поднимется ровно на столько, чему равен объем тела
Пользуясь измерительным цилиндром, нельзя забывать, что это прибор, имеющий шкалу, а значит, результат получится с погрешностью.
Числа «карлики» и числа «великаны»
 Солнечная система. Лапка мухи под микроскопом.
Солнечная система. Лапка мухи под микроскопом.
Чтобы достать до Альфа Центавры, звезды, ближайшей к Солнечной системе, надо со скоростью света (300 000 км/с) лететь четыре года. Расстояния до небесных тел огромны.
 К звездам. (Источник)
К звездам. (Источник)
Если определить расстояние от Земли до Солнца, то оно выразится числом 150 000 000 000 м. А бывают числа с еще большим количеством нулей. Масса Земли в килограммах выражается числом с 24 нулями. Такие числа называют «гигантами». Их записывать и использовать очень неудобно.
Существует способ краткой записи больших чисел в виде степени. Например, 1 000 000 = 106. 10 – основание, а 6 – показатель степени.
Используя этот способ, расстояние от нашей планеты до Солнца запишется так:
150 000 000 000 = 15 ∙ 1010 м – это промежуток называется астрономической единицей (1 а.е.) и служит единицей сравнения в Солнечной системе.
До Альфа-Центавры расстояние в 270 000 а.е., или 4 световых года. Световой год – это тоже астрономическая единица измерения расстояния. Астрономия – наука о космосе и космических телах. (1 св. год = 9,46 ∙ 1015 м = 68 000а.е.).
 Фото двойной звезды Альфа созвездия Центавра. (Источник)
Фото двойной звезды Альфа созвездия Центавра. (Источник)
Большие числа записываются при помощи кратных приставок. Например, километр – это тысяча метров, килограмм – тысяча граммов. Приставка «кило» обозначает «тысяча». Есть и другие приставки, которые обозначают умножение величины на число, кратное десяти. Примеры и форма записи даны в таблице кратных приставок.
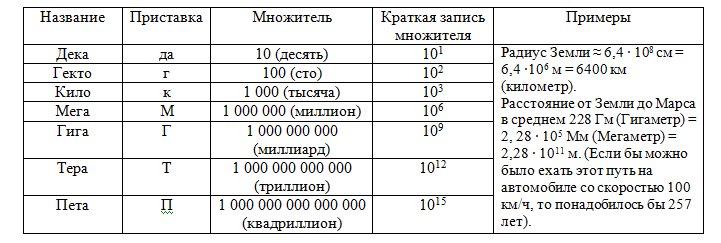
Используя эти приставки можно записывать очень большие числа.
1 а.е. = 150 000 000 000 м = 150 ∙ 109 м = 150Гм;
1 св. год = 9 460 000 000 000 м = 9,46 ∙ 1012 м = 9,46 Тм;
А теперь о числах – «карликах». Если сделать попытку измерить толщину одного листа книги, то сразу это не получится. Надо действовать по простому плану:
- отобрать в книге некоторое число страниц N (N = 100, например);
- измерить толщину L этих страниц (пусть L = 11 мм);
- найти толщину одной страницы d по формуле d = L/N.
Получится d = 0,11 мм = 0, 00011 м. Это число очень маленькое.
Такой способ измерения малых величин называется методом рядов. Он достаточно прост.
 Размеры пшена. Толщина проволоки.
Размеры пшена. Толщина проволоки.
Но существуют и гораздо меньшие величины. Маленькие числа, так называемые «карлики», также записывают при помощи степеней или дольных приставок. (С приставками деци, санти, милли знакомятся еще в начальной школе).
Число меньше единицы, поэтому показатель степени – отрицательное число. Оно показывает количество цифр после запятой. Например, 0, 00011 м = 11 ∙ 10-5 м.
Число 0,00000625 можно записать по-разному, применяя степень:
625 ∙ 10-8, 62,5 ∙ 10-7, 6,25 ∙ 10-6 и т. д.
Очень маленькие числа по-другому можно записывать, используя таблицу дольных приставок.
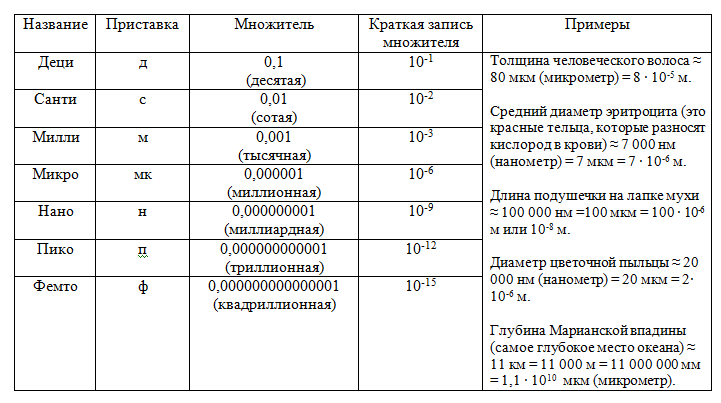
Например, при изготовлении сверхточных приборов (телескопов, микроскопов и др.), детали ошлифовываются до очень гладкой поверхности. Неровности должны быть меньше 2,5 ∙ 10-6 м или 2,5 мкм.
Большие и маленькие числа помогают человеку в различных отраслях деятельности: в науке, промышленности, медицине и т.д.
Площадь и ее измерение
С измерением длин очень тесно связано измерение площадей. Из математики известны формулы площадей квадрата и прямоугольника. У квадрата все стороны равны, поэтому достаточно измерить одну сторону, а у прямоугольника противоположные стороны равны, поэтому надо знать длину и ширину. Площадь обозначается буквой S, и формулы для расчета площадей следующие:
Sкв = a2, Sпр = а ∙ в. Единицей измерения площади является квадратный метр (м2).
Для измерения малых площадей применяются см2 и мм2, а большие площади – в км2. В сельском хозяйстве для измерения земельных участков используют внесистемные единицы: гектар (га) – для больших, ар (а) или «сотка» — для небольших (приусадебных или дачных) участков земли. 1га = 10 000 м2, 1 а = 100 м2.
Очень часто на практике имеют дело с различными кругами. Это может быть цирковая арена, крышка стола, разрез ствола дерева. Формула нахождения площади круга: S = πR2. (π (пи) – это бесконечная дробь ≈ 3,14 подробно изучается в курсе алгебры).
Арена цирка. Круглый стол. Спил дерева.
А как определить площадь, ограниченную произвольной кривой линией? Такая площадь может быть у озера, полянки в лесу, листочка с дерева.
Существует правило нахождения площади тел произвольной формы:
- Разбить всю поверхность на равные квадраты с известной площадью.
- Подсчитать количество целых квадратов.
- Подсчитать число нецелых квадратов и поделить это число на два. (Это будет примерное количество целых квадратов).
- Сложить результаты пунктов 2 и 3.
- Умножить площадь одного квадрата на общее число целых квадратов.
Площадь больших территорий изображают в условном масштабе или фотографируют, применяют прием разбиения на квадраты и находят площадь фотографии. Используя масштаб вычисляют реальную площадь поверхности.
Довольно часто площадь приходится находить в географии. Каждое государство, область, город имеют свои площади. В строительстве – любое здание имеет площадь, которую необходимо знать строителям. В сельском хозяйстве ведется постоянный учет площадей для посевных культур.
Является ли вода полярной или неполярной?
 Химическая структура молекулы воды.
Химическая структура молекулы воды.
Такое расположение молекулы воды создает положительно заряженную сторону около атомов водорода и отрицательно заряженную сторону около атома кислорода.
Когда две молекулы воды соединяются вместе, положительная сторона одной молекулы присоединяется к отрицательной стороне другой. Когда это делается в больших масштабах (то есть с миллионами молекул воды), получается уникальная структура, объясняющая некоторые химические свойства воды.
В жидком состоянии молекулы воды могут свободно перемещаться, образуя и разрывая водородные связи, что объясняет неправильную форму воды (или любой другой жидкости, если на то пошло). Некоторые молекулы воды часто «накладываются» друг на друга, что объясняет более высокую плотность воды по сравнению со льдом.
 Расположение молекул воды в жидком состоянии.
Расположение молекул воды в жидком состоянии.
Однако по мере снижения температуры и охлаждения воды межмолекулярные силы увеличиваются, свобода движения молекул воды уменьшается, и они становятся все менее и менее энергичными (по мере снижения температуры).
Когда вода достигает точки замерзания, движение ее молекул становится незначительным, и они приобретают более определенную форму, устроенную в виде гексагональных решеток.
Ниже представлен упрощенный вариант расположения молекул воды в кристаллической форме во льду:
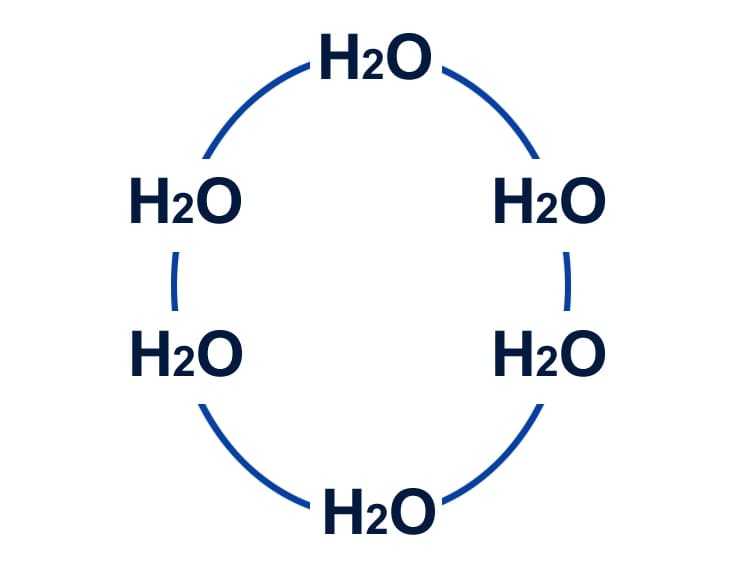 Расположение молекул воды в твердой форме.
Расположение молекул воды в твердой форме.
Это кристаллическое расположение молекул воды менее плотное, потому что оно предотвращает накопление молекул (как в жидкой форме) из-за более сильных межмолекулярных сил.
Это расстояние между молекулами и их фиксация в этом положении увеличивает объем воды, поэтому говорят, что вода расширяется при замерзании.
Лабораторная работа № 4 «Измерение объема тела» 7 класс.
Ищем педагогов в команду «Инфоурок»
Лабораторная работа № 4 «Измерение объема тела».
Цель работы: научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы: измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайка, болтик и т.д.).
ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ И ВОПРОСЫ
При погружении в мензурку тела уровень воды в мензурке повышается, так как увеличивается объём воды на величину, равную объёму тела.
Определите по рисунку уровень воды:
до погружения ______________
после погружения _____________
Объём тела ____________________
Какую физическую величину измеряют с помощью мензурки?
В каких единицах она измеряется?
1м³ = ____________ см³ 0,01 м³ = __________ см³
1 см³ = ___________ м³ 100 см³ = __________ м³
0,5 м³ = ___________ см³ 5000 см³ = __________ м³
Определите цену деления мензурки.
Цена деления = ______________
Налейте в мензурку столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте объём . Результат занесите в таблицу.
Опустите тело в воду, удерживая его за нитку, и снова измерьте объём жидкости . Результат занесите в таблицу.
Посчитайте объём тела . Занесите в таблицу.
То же самое проделайте с другими имеющимися у вас телами.
Начальный объём воды , см³
Объём воды и тела , см³
Лабораторная работа № 4 «Измерение объема тела».
Цель работы: научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы: измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайка, болтик и т.д.).
ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ И ВОПРОСЫ
При погружении в мензурку тела уровень воды в мензурке повышается, так как увеличивается объём воды на величину, равную объёму тела.
Определите по рисунку уровень воды:
Какую физическую величину измеряют с помощью мензурки? Объем тела
В каких единицах она измеряется? мл
1м³ = 1000000 см³ 0,01 м³ = 10000 см³
1 см³ = 0,000001 м³ 100 см³ = 0,0001 м³
0,5 м³ = 500000 см³ 5000 см³ = 0,005 м³
Определите цену деления мензурки.
Налейте в мензурку столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте объём . Результат занесите в таблицу.
Опустите тело в воду, удерживая его за нитку, и снова измерьте объём жидкости . Результат занесите в таблицу.
Посчитайте объём тела . Занесите в таблицу.
То же самое проделайте с другими имеющимися у вас телами.
Начальный объём воды , см³
Объём воды и тела , см³
Вывод: Объем тела неправильной формы можно определить с помощью измерительного цилиндра. Для этого определяют объем воды в мензурке, затем объем воды и тела, погруженного в нее. Объем тела приближенно равен разности этих объемов.
Международная дистанционная олимпиада Осень 2021
Вам будут интересны эти курсы:
Оставьте свой комментарий
В Туве объявили каникулы в школах с 25 октября
Школьников не планируют переводить на удаленку после каникул
Минобрнауки утвердило перечень олимпиад для школьников на 2021-2022 учебный год
Гинцбург анонсировал регистрацию детской вакцины от COVID-19
Власти Амурской области предложили продлить каникулы в школах в связи с эпидобстановкой
В школе в Пермском крае произошла стрельба
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Преимущества онлайн-пособия по Физике для 7 класса Перышкин, Вертикаль Базовый уровень Дрофа
Онлайн-гдз станут незаменимым помощником в изучении этого увлекательного предмета. Объемная и информационно насыщенная, она предоставит ребятам возможность более глубокого погружения в материал и углубленного понимания важнейших тем. На уроках ученики будут знакомиться с новым материалом и в дальнейшем глубже изучать следующие темы дома. Кинематика точки и твердого тела – одна из важнейших тем в физике. Ребята будут изучать различные аспекты движения объектов и его характеристики. Относительность движения также является неотъемлемой частью физики. Ученики смогут понять, как взаимосвязаны движущиеся объекты и как меняется их взаимное положение. Нужно знать каждому учащемуся:
- Этот сборник был разработан известными и опытными методистами, которые обладают богатым опытом в области физики для старшей школы. Вся информация, представленная в онлайн-гдз, неоднократно проверена и прошла проверку на достоверность.
- Неоспоримым преимуществом этого сборника является его соответствие требованиям Федерального государственного образовательного стандарта (ФГОС). Это гарантирует, что все представленные материалы не только полно исследованы, но и соответствуют актуальным нормам и стандартам образования.
- Этот сборник, содержащий верные ответы и решения, может быть полезен не только учащимся, но и учителям в их профессиональной деятельности. Благодаря обширному спектру упражнений, представленных в данной тетради, вы сможете найти решения заданий любой степени сложности.
Таким образом, этот сборник может стать незаменимым помощником в освоении физики для всех старшеклассников и учителей в их учебном процессе.
Презентация на тему: » Лабораторная работа «Измерение объема с помощью измерительного цилиндра» Лабораторная работа «Измерение объема с помощью измерительного цилиндра» МОУ «Стародворская.» — Транскрипт:
1
Лабораторная работа «Измерение объема с помощью измерительного цилиндра» Лабораторная работа «Измерение объема с помощью измерительного цилиндра» МОУ «Стародворская СОШ» с.Старый Двор с.Старый Двор Суздальский район Панина Л.А. Панина Л.А.

2
Цель работы: научиться определять объем тела с помощью измерительного цилиндра.

3
Оборудование: Мензурка Мензурка Стакан лабораторный 2 шт. Стакан лабораторный 2 шт. Ластик Ластик Гайка Гайка Камень Камень Пластилин Пластилин Линейка Линейка Металлический цилиндр Металлический цилиндр Деревянный брусок (малый) Деревянный брусок (малый) Соль Соль Резинка – 2 шт. Резинка – 2 шт. Отливной стакан. Отливной стакан.

4
Задание 1.Измерение емкости бутылочки Определите цену деления мензурки Определите цену деления мензурки Заполните бутылочку водой Заполните бутылочку водой Вылейте воду в мензурку и определите объем бутылочки Вылейте воду в мензурку и определите объем бутылочки Результат запишите в таблицу Результат запишите в таблицу Цена деления мензурки см³ см³ Объем мензурки V см³

5
Дополнительное задание Дополнительное задание Можно ли утверждать, что общий объем воды равен сумме 2-х объемов? Можно ли утверждать, что общий объем воды равен сумме 2-х объемов? V=V+V V=V+V Сделайте вывод: _______________ Цена деления мензурки см³ Объем воды в 1 стакане см³ см³ Объем воды в 2 стакане см³ см³ Общий объем см³

6
Дополнительное задание Дополнительное задание Подумайте, что произойдет с объемом соли и воды при смешивании? Подумайте, что произойдет с объемом соли и воды при смешивании? 1.Насыпать в один стакан соль до половины и отметить уровень соли. 2. Налейте в другой стакан воду до половины. 3. Сделайте предположение
4.Осторожно вылейте воду в стакан с солью, растворите соль в воде. 5
Сделайте вывод: ___________________
7
Задание 2. «Измерение объема тела» Налейте воду в мензурку и определите объем воды (V в) Налейте воду в мензурку и определите объем воды (V в) Опустите в воду тело и определите объем воды и тела (V в, т) Опустите в воду тело и определите объем воды и тела (V в, т) Вычислите объем тела (Vт) Вычислите объем тела (Vт) Измеряемое тело Объем воды Vв см³ см³ Объем воды и тела V в, т см³ V в, т см³ Объем тела Vт, см³ Vт =V в,т -Vв

8
Дополнительное задание Дополнительное задание Определите объем тела правильной формы 2-мя способами: Определите объем тела правильной формы 2-мя способами: 1. С помощью линейки; a V= a V= b c b c 2. С помощью мензурки. V= Совпадают ли результаты измерений? Сделайте вывод: ____________

9
Дополнительное задание Дополнительное задание Определите объем цилиндрического тела Определите объем цилиндрического тела 1. Измерьте диаметр цилиндра d V=S дна *h цилиндра = π*d³/4*h V=S дна *h цилиндра = π*d³/4*h 2. Определите объем цилиндра с помощью мензурки. 3.Сравните результаты, сделайте вывод.

10
Дополнительное задание Дополнительное задание Зависит ли объем тела от его формы? Зависит ли объем тела от его формы? 1. Слепите из пластилина шарик и с помощью мензурки определите его объем Vш. 2. Слепите из пластилина куб и определите его объем с помощью мензурки Vк. 3.Слепите из пластилина тело неправильной формы и измерьте его объем Vт. 4. Что происходит с объемом тела при изменении формы? Сделайте вывод?

11
Задание 3 «Определение объема тела, не помещающегося в мензурке» Опустите тело в отливной стакан. Опустите тело в отливной стакан. Определите объем воды, вытесненной телом с помощью мензурки. Определите объем воды, вытесненной телом с помощью мензурки. Сделайте вывод по цели работы. Сделайте вывод по цели работы.

Определение площади и объема в физике с примером
Определение площади и объема:
В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски.
Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.
Рис. 6.1.
Рис. 6.2.
Рис. 6.3
Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле: S = a · b, (6.1) где a – ширина прямоугольника, b – высота.
Площадь параллелограмма ABCD (рис. 6.2) также находится по формуле 6.1. Площадь квадрата найти легко, поскольку его ширина и высота одинаковы: S = a · a = a 2 , (6.2)
Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле:
Проблема определения площади круга была решена еще в Древней Греции. Для этого нужно знать радиус круга и число «пи», приблизительное значение которого π ≈ 3,14. Площадь круга равняется S = π · R 2 , (6.4) .
Значение числа
Молекулы воды требуют больше места
Причина, по которой происходят эти процессы расширения и сжатия различных веществ, — это молекулы. Те, что получают больше энергии (это происходит в теплой комнате), движутся намного быстрее, чем молекулы в холодной комнате. Частицы с большей энергией сталкиваются гораздо активнее, и им требуется больше места для перемещения. Чтобы сдержать давление, оказываемое молекулами, материал начинает увеличиваться в размерах. К тому же это происходит довольно быстро. Итак, вода расширяется или сжимается при замерзании? Почему это происходит?
Вода этим правилам не подчиняется. Если мы начнем охлаждать воду до четырех градусов Цельсия, то ее объем уменьшится. Но если температура продолжает падать, вода внезапно начинает расширяться! Есть такое свойство, как аномалия плотности воды. Это свойство проявляется при температуре четыре градуса Цельсия.

Теперь, когда мы понимаем, расширяется или сжимается вода при замерзании, давайте выясним, как на самом деле возникает эта аномалия. Причина кроется в частицах, из которых он состоит. Молекула воды состоит из двух атомов водорода и одного атома кислорода. Все знают формулу воды с начальной школы. Атомы этой молекулы по-разному притягивают электроны. Водород создает положительный центр тяжести, а кислород — отрицательный. Когда молекулы воды сталкиваются друг с другом, атомы водорода одной молекулы передаются атому кислорода совершенно другой молекулы. Это явление называется водородной связью.
Вычисление объема простых фигур
Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):
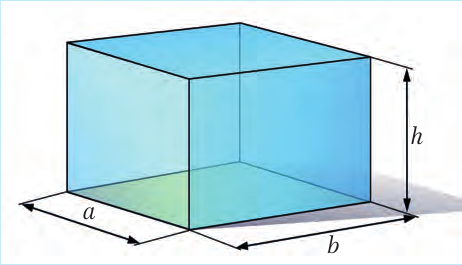
Рис. 6.4.
Рис. 6.5.
Рис. 6.6.
V = a · b · h (6.4) Поскольку S = a · b, где S – это площадь основания ящика, то формулу (6.4) можно переписать и так:
V = S · h (6.5) У куба все ребра равны, потому его объем равняется: V = a · a · a = a 3 (6.6)
Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть: V = S · h = πR 2 · h (6.7)
Объем шара (рис. 6.6)




























