Конструктивные элементы деталей

Преимущества и недостатки различных геометрических тел в формировании деталей

При создании различных деталей и изделий используются разные геометрические формы

Каждая из них имеет свои преимущества и недостатки, которые важно учитывать при выборе подходящей формы для конкретного изделия

Преимущества и недостатки куба:

Куб является одним из самых простых геометрических тел. Он имеет ровные грани, что облегчает его изготовление и монтаж. Кубы устойчивы и прочны, поэтому хорошо подходят для создания деталей, которые будут испытывать большие нагрузки.

Однако, у куба есть и некоторые недостатки. Из-за своей симметричной формы, куб не всегда идеально вписывается в сложные конструкции и требует больших затрат на приспособления и крепления. Также, из-за своей геометрии, куб трудно использовать для создания сложных форм и изгибов.

Преимущества и недостатки цилиндра:

Цилиндр является одной из самых распространенных геометрических форм в машиностроении и строительстве. Он имеет круглую или овальную форму, что позволяет ему легко вписываться в различные конструкции. Цилиндры прочны и устойчивы, что делает их идеальными для монтажа деталей, работающих на нагрузку.

Однако, у цилиндра также есть некоторые недостатки. Из-за своей геометрии, цилиндры сложнее производить и монтажировать, особенно в сложных конструкциях. Также, цилиндры не являются идеальным выбором для деталей, требующих сложной формы или изгибов.

Преимущества и недостатки пирамиды:

Пирамиды могут быть разных форм и размеров, но обычно они имеют треугольную основу и четыре треугольных грани. Пирамиды легко вписываются в различные конструкции и имеют отличные прочностные характеристики, что делает их подходящими для строительных и машиностроительных деталей.

Однако, у пирамиды есть и некоторые недостатки. Из-за своей формы, пирамида может быть сложной в производстве и монтаже, особенно в случае сложных конструкций. Также, из-за отсутствия плоских граней, пирамиды менее устойчивы и могут быть более подвержены деформации и ломке.

Преимущества и недостатки сферы:

Сфера имеет круглую форму и не имеет плоских поверхностей. Она обладает максимальным объемом при заданной площади границы, что делает ее идеальным выбором для создания контейнеров или сосудов.

Однако, сфера также имеет свои недостатки. Из-за своей формы, сферы сложнее в монтаже и требуют специальных приспособлений. Также, сферы могут быть менее устойчивыми и более подверженными деформации и ломке.

Геометрическое тело	Преимущества	Недостатки
Куб	— Прочность и устойчивость— Легкость монтажа	— Ограниченные возможности для сложных форм— Требуются дополнительные крепления
Цилиндр	— Вписывается в различные конструкции— Прочность и устойчивость	— Сложность производства и монтажа— Ограниченные возможности для сложных форм
Пирамида	— Вписывается в различные конструкции— Прочность и устойчивость	— Сложность производства и монтажа— Менее устойчивы и более подвержены деформации
Сфера	— Максимальный объем при заданной площади границы	— Сложность монтажа— Менее устойчивы и более подвержены деформации

При выборе геометрической формы для деталей важно учитывать их функциональные требования, а также технологические возможности производства и монтажа

Задачи для самостоятельного решения

Задача 1

Установить класс кинематической пары, образуемой
плоской (1) и конической (2) поверхностями (конус касается плоскости только вершиной).
По отношению к координатным осям xyzперечислить
все виды допускаемых движений конуса относительно плоскости.

Задача2

Для плоской кинематической пары, представленной на рисунке,
установить:

— высшая пара, или низшая;

— класс кинематической пары;

— число подвижностей в относительном движении звеньев
1 и 2.

Задача3

Конус 2 касается плоскости 1 своей образующей. Для
кинематической пары, образуемой указанными звеньями, установить класс и число
подвижностей в относительном движении звеньев 1 и 2 (назвать эти подвижности по
отношению к какой-либо системе координат, связанной с плоскостью).

Задача 4

Конус 2 касается плоскости 1 кромкой своего основания,
вершина конуса s удалена от плоскости на расстояние где – проекция
вершины конуса на плоскость. Для кинематической пары, образуемой указанными
звеньями, установить класс и число подвижностей в относительном движении
звеньев 1 и 2 (назвать эти подвижности по отношению к какой-либо системе
координат, связанной сплоскостью).

Задача 5

Для механизма с одной степенью свободы указать номера
звеньев, образующих группу III класса 3-го
порядка при начальном звене 9.

Задача6 (см.
рисунок к задаче 5)

Для механизма с одной степенью свободы указать номера
звеньев, образующих группу III класса 3-го
порядка при начальном звене 4.

Задача7 (см.
рисунок к задаче 5)

Для механизма с одной степенью свободы написать
формулу строения механизма при начальном звене 5.

Задача8

Для механизма с одной степенью свободы пронумеровать
звенья и написать формулу строения механизма при начальном звене OA.

Задача 9

Считая звено 1 начальным, указать структурную группу,
которую можно отсоединить от механизма, не нарушая его подвижности (ответ
обосновать).

Задача 10 (см. рисунок к задаче 9)

Считая звено 2 начальным, указать структурную группу,
которую можно отсоединить от механизма, не нарушая его подвижности (ответ
обосновать).

Задача 11

Задача 12 (см. рисунок к задаче 11)

Для механизма с одной степенью свободы указать номера
звеньев, образующих группу III класса 3-го
порядка при начальном звене 5.

Задача 13 (см. рисунок к задаче 11)

Считая звено 9 начальным, указать структурную группу,
которую можно отсоединить от механизма, не нарушая его подвижности (ответ
обосновать).

Задача 14

Считая звено 1 начальным, указать две первые
структурные группы, которые можно поочередно отсоединить от механизма, не
нарушая его подвижности (ответ обосновать).

Задача 15

Задача 16 (см. рисунок к задаче 15)

Для механизма с одной степенью свободы указать номера
звеньев, образующих группу III класса 3-го
порядка при начальном звене 6.

Задача 17 (см. рисунок к задаче 15)

Задача 18

Задача 19 (см. рисунок к задаче 18)

Считая звено 5 начальным, указать две первые
структурные группы, которые можно поочередно отсоединить от механизма, не
нарушая его подвижности (ответ обосновать).

Задача 20 (см. рисунок к задаче 18)

Считая звено 3 начальным, указать две первые
структурные группы, которые можно поочередно отсоединить от механизма, не
нарушая его подвижности (ответ обосновать).

Задача 21 (см. рисунок к задаче 18)

Считая звено 5 начальным, указать номера звеньев,
образующих группу III класса 3-го порядка.

Задачи 22 –
24

Для механизма с высшей кинематической парой построить
заменяющий механизм; замену высшей пары произвести непосредственно на
кинематической схеме. Написать формулу строения заменяющего механизма при
начальном звене 4.

Задачи 25 –
30

Если изображенная кинематическая цепь является
структурной группой, указать ее класс и порядок (в противном случае объяснить,
почему цепь не является группой).

Направляющая 1 в состав кинематической цепи не входит

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Строительная механика Детали машин
Теория машин и механизмов

00:00:00

Геометрическое тело «Параллелепипед»

У параллелепипеда три оси: длина, ширина и высота. Все его грани плоские и состоят из прямоугольников. Грани противоположных сторон параллелепипеда параллельны друг другу.

Параллелепипед имеет восемь вершин, двенадцать ребер и шесть граней. Все ребра параллелепипеда пересекаются перпендикулярно своим соседним ребрам.

Геометрические тела, образованные в форме параллелепипеда, широко используются в инженерии, строительстве, архитектуре и многих других областях. Их простая форма и прямоугольные грани делают их удобными для создания и расчета различных конструкций и моделей.

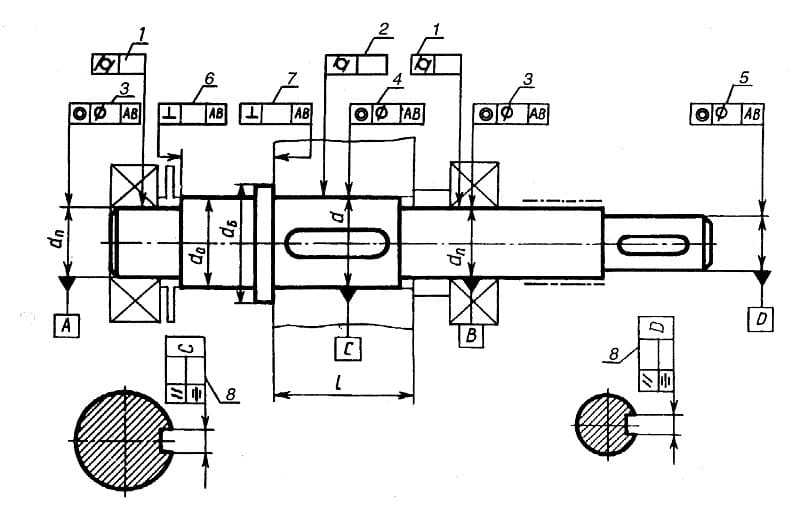
6 Задачи к теме 7(шпоночные соединения)

Для шпоночных соединений с
призматическими шпонками подобрать номинальные размеры шпонок и пазов под них.
Назначить посадки и предельные отклонения на все детали соединения. Определить
предельные зазоры и натяги между деталями. Построить схемы полей допусков.

Вариант	Диаметр вала, мм	Длина шпонки L, мм	Поле допуска шпонки	Поле допуска паза вала	Поле допуска паза втулки
10	100	220	h9	P9	P9

1) По
таблицам ГОСТ 23360 – 78 находим размеры:

ширина шпонки b = 28 мм;
высота шпонки h = 16 мм; глубина паза на валу t₁
= 10 мм; глубина паза во втулке t₂ = 6,4 мм.

2) По таблице для призматических
шпонок при нормальном соединении

Цилиндрические поверхности создают выпуклые и вогнутые кривизны

Цилиндрические поверхности широко используются в проектировании и изготовлении различных деталей, благодаря своей универсальной форме и возможности создания как выпуклых, так и вогнутых кривизн. Цилиндрическая поверхность образуется вращением прямой линии, называемой образующей, вокруг своей оси. Она состоит из всех точек, лежащих на заданном расстоянии от оси.

При создании выпуклой кривизны цилиндрическая поверхность выпуклается в определенных направлениях, что позволяет создавать детали с плавными изгибами. Такие детали могут иметь различные приложения, от автомобильных кузовов до компьютерных корпусов. Выпуклые цилиндрические поверхности создают элегантные и эстетичные формы, привлекательные для взгляда.

С другой стороны, цилиндрические поверхности также могут быть вогнутыми, что означает, что они выпуклые в определенных направлениях. Это позволяет создавать детали с внутренними изгибами или пустотами. Такие детали могут использоваться, например, для создания внутренних полостей внутри механизмов или для создания кривых поверхностей для оптимизации аэродинамических характеристик.

Таким образом, цилиндрические поверхности предоставляют инженерам и дизайнерам широкий спектр возможностей для создания форм и кривизн в деталях. Они могут быть использованы как для создания гладких и элегантных форм, так и для создания сложных криволинейных конструкций. При проектировании деталей следует учитывать возможности, предоставляемые цилиндрическими поверхностями, и на основе них создавать уникальные и функциональные формы.

Использование основных геометрических тел в конструкции детали

При разработке и проектировании различных деталей и механизмов, инженеры и конструкторы часто используют основные геометрические тела. Это позволяет создать конструкции с определенными свойствами и характеристиками, обеспечивая необходимую прочность, устойчивость и функциональность.

Одним из наиболее распространенных геометрических тел, используемых в конструкциях, является параллелепипед. Это прямоугольный параллелепипед, у которого все грани являются прямоугольниками. Параллелепипеды используются для создания прочных и жестких конструкций, например, корпусов различных устройств, ящиков, рамок и т.д.

Еще одно широко применяемое геометрическое тело — цилиндр. Цилиндр имеет два основания, которые представляют собой круги одинакового радиуса, и боковую поверхность, которая является поверхностью вращения. Цилиндры используются, например, в деталях двигателей, гидравлических системах и вентиляционных системах.

Конус также является одним из основных геометрических тел, применяемых в конструкции деталей. Он имеет основание, являющееся кругом, и боковую поверхность, которая сужается к вершине. Конусы используются в различных областях, например, внутри двигателей, светильниках, а также в деталях гидравлических и пневматических систем.

Сфера — это другое геометрическое тело, широко применяемое в конструкции деталей. Сфера представляет собой геометрическое тело, у которого все точки находятся на одинаковом расстоянии от центра. Сферы используются в шарнирах, подшипниках, вентилях и различных оболочках.

Кроме основных геометрических тел, существуют и другие, менее распространенные, которые также используются в конструкциях деталей. Например, пирамида, тор, трубка и другие.

Использование основных геометрических тел в конструкции детали позволяет инженерам и конструкторам создавать надежные и функциональные изделия. При выборе геометрического тела для конструкции необходимо учитывать требуемые свойства и характеристики детали, а также ее функциональное назначение.

Конструктивные формы — деталь

Конструктивные формы деталей, исключающие опасность коробления и появления трещин, изображены на фиг.

Конструктивные формы деталей должны обеспечивать не только минимальный расход материала, но и такое его распределение, при котором достигается достаточная прочность деталей во всех частях. Однако проч ность деталей зависит не только от выбора соответствующих материалов и сечений стенок, но и от применения ребер жесткости, что часто дает эко-номию веса деталей за счет уменьшения толщины стенок, в результате чего снижается время выдержки в прессформе.

Конструктивные формы деталей должны давать возможность в процессе изготовления заготовок получать в последних устойчивое постоянство форм и размеров. Соблюдение этого условия в особенности необходимо в серийном и массовом производстве, при котором неустойчивость размеров в заготовках делает затруднительным, а иногда и невозможным их правильное базирование в приспособлениях для последующей механической обработки.

Конструктивные формы деталей, полученных литьем по выплавляемым ртутным моделям, по сравнению с литыми в землю показаны на фиг.

Конструктивные формы деталей должны обеспечивать не только минимальный расход материала, но и такое его распределение, при котором достигается достаточная прочность деталей во всех частях. Однако прочность деталей зависит не только от выбора соответствующих материалов и сечений стенок; ее можно повысить применением ребер жесткости, что дает также экономию веса деталей за счет уменьшения толщины стенок, снижает время выдержки в пресс-форме и противодействует короблению.

Конструктивные формы детали должны обеспечить по возможности равнопрочность всех ее сечений.

Если конструктивные формы детали или узла не позволяют осуществить зажатие в тисках, последние нередко используются для закрепления разнообразных оправок или специальных зажимов, удерживающих собираемые узлы при выполнении сборочной операции.

Анализ поверхностей, образующих конструктивные формы деталей, на основе функций, выполняемых ими при работе деталей в машине, показывает, что эти поверхности выполняют различное назначение, в зависимости от которого их можно разделить на четыре вида.

Из изложенного следует, что конструктивные формы деталей и всей машины в целом следует разрабатывать, исходя: 1) из их служебного назначения и 2) из требований технологии их наиболее экономичного изготовления.

Кроме того, следует учитывать, что конструктивные формы деталей оказывают непосредственное влияние на величину усадки.

В силу изложенного нужно подчеркнуть, что конструктивные формы детали являются не только производными функционального ее назначения, но в известной степени зависит от способов изготовления детали и требуемого веса ее. Поэтому при конструировании деталей машин необходимо исходить из предпосылки, что одна и та же конструктивная задача может иметь несколько технологических решений, различных по трудоемкости.

Следует отметить, что требуемая точность формы поверхностей, образующих конструктивные формы детали, выше точности размеров детали. Ввиду этого рассматривалась точность формы, а именно плоскостность.

Основными критериями, определяющими выбор материала для изготовления литых деталей, являются конструктивные формы деталей, их целевое назначение и условия работы, характер и величина нагрузок и напряжений.

При конструировании ряда облицовочных деталей машин, в особенности облицовочных деталей автомобилей, конструктивные формы деталей обусловливаются в первую очередь соображениями чисто эстетического характера. В силу этих соображений приходится отступать от многих перечисленных выше желательных условий штамповки-вытяжки, однако в такой мере, чтобы штамповка оказывалась все же возможной.

Квалитет

Квалитет (в русском от нем. Qualität, которое от лат. qualitas — качество) — характеристика точности изготовления изделия (детали), определяющая значения допусков.

Квалитет является мерой точности. С увеличением квалитета допуск увеличивается, а точность понижается.

Допуск по квалитету обозначается буквами IT с указанием номера квалитета, например IT8 — допуск по 8-му квалитету.
- Квалитеты с 01 до 4-го используются для изготовления калибров и контркалибров.
- Квалитеты от 5-го до 12-го применяют для изготовления деталей, образующих сопряжения — относительные положения составных частей изделия, характеризуемые соприкосновением их поверхностей или зазором между ними, заданными конструкторской документацией. Примером таких сопряжений могут быть, ГЦС — гладкие цилиндрические соединения).
- Квалитеты от 13-го до 17-го используют для параметров деталей, не образующих сопряжений и не оказывающих определяющего влияния.
Основная закономерность построения допусков размеров (допуск обозначается IT = International tolerance),
- IT, мкм = K * i,
- где K — квалитет (число единиц допуска), i — единица допуска, мкм.
На диаметры от 1 до 500 мм единица допуска функционально связана с номинальным размером i=0.45D3+0.001D{\displaystyle i=0.45{\sqrt{D}}+0.001D}, мкм.
Соответствующие значения допуска регламентируются стандартом на допуски и посадки (Limits and Fits) ISO 286-1:2010, а также ГОСТ 25346-89..

Значение допусков для размеров основного отверстия до 500 мм:

Размер, мм	Допуск, мкм, при квалитете
01	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
До 3	0,3	0,5	0,8	1,2	2	3	4	6	10	14	25	40	60	100	140	250	400	600	1000
3—6	0,4	0,6	1	1,5	2,5	4	5	8	12	18	30	48	75	120	180	300	480	750	1200
6—10	0,4	0,6	1	1,5	2,5	4	6	9	15	22	36	58	90	150	220	360	580	900	1500
10—18	0,5	0,8	1,2	2	3	5	8	11	18	27	43	70	110	180	270	430	700	1100	1800
18—30	0,6	1	1,5	2,5	4	6	9	12	21	33	52	84	130	210	330	520	840	1300	2100
30—50	0,6	1	1,5	2,5	4	7	11	16	25	39	62	100	160	250	390	620	1000	1600	2500
50—80	0,8	1,5	2	3	5	8	13	19	30	46	74	120	190	300	460	740	1200	1900	3000
80—120	1	1,5	2,5	4	6	10	15	22	35	54	87	140	220	350	540	870	1400	2200	3500
120—180	1,2	2	3,5	5	8	12	18	25	40	63	100	160	250	400	630	1000	1600	2500	4000
180—250	2	3	4,5	7	10	14	20	29	46	72	115	185	290	460	720	1150	1850	2900	4600
250—315	2,5	4	6	8	12	16	23	32	52	81	130	210	320	520	810	1300	2100	3200	5200
315—400	3	5	7	9	13	18	25	36	57	89	140	230	360	570	890	1400	2300	3600	5700
400—500	4	6	8	10	15	20	27	40	63	97	155	250	400	630	970	1550	2500	4000	6300

Дополнительные варианты назначения предельных отклонений линейных размеров с неуказанными допусками

А.1 Настоящее приложение устанавливает дополнительные варианты предельных отклонений линейных размеров с неуказанными допусками, нашедшие применение в промышленности.

Кроме симметричных предельных отклонений, установленных в основной части стандарта, в дополнение к ИСО 2768-1 допускается применение односторонних предельных отклонений для размеров отверстий и валов по квалитетам ГОСТ 25346 и ГОСТ 25348 (дополнительный вариант 1) или классам точности настоящего стандарта (дополнительный вариант 2) в соответствии с таблицей .

Назначение дополнительных вариантов предельных отклонений линейных размеров с неуказанными допусками при новом проектировании рекомендуется ограничить.

Таблица А.1 — Дополнительные варианты неуказанных предельных отклонений линейных размеров

Класс точности

Обозначения предельных отклонений

размеров отверстий

размеров валов

размеров элементов, не относящихся к отверстиям и валам

Точный

Н12

h12

± t₁/2 (или ± IT12/2)

Средний

Н14

h14

± t₂/2 (или ± IT14/2)

Грубый

Н16

h16

± t₃/2 (или ± IT16/2)

Очень грубый

Н17

h17

± t₄/2 (или ± IT17/2)

Точный

+ t₁

— t₁

± t₁/2

Средний

+ t₂

— t₂

± t₂/2

Грубый

+ t₃

— t₃

± t₃/2

Очень грубый

+ t₄

— t₄

± t₄/2

А.2 Предельные отклонения по квалитетам (Н, h, ± IT/2) должны соответствовать ГОСТ 25346 и ГОСТ 25348.

Симметричные предельные отклонения по классам точности (± t/2) должны соответствовать приведенным в таблице , при этом обозначение ± t₁/2 соответствует обозначению f, ± t₂/2 — т, ± t₃/2 — с, ± t₄/2 — v.

Односторонние предельные отклонения (+t, —t) должны соответствовать приведенным в таблице .

Таблица А.2 — Односторонние предельные отклонения линейных размеров, кроме притупленных кромок (наружных радиусов скругления и высот фасок, см. таблицу ) по классам точности

Размеры в миллиметрах

Класс точности	Обозначение предельных отклонений	Предельные отклонения для интервалов номинальных размеров
от 0,5 до 3	св. 3 до 6	св. 6 до 30	св. 30 до 120	св. 120 до 400	св. 400 до 1000	св. 1000 до 2000	св. 2000 до 4000	св. 4000 до 6000	св. 6000 до 8000	св. 8000 до 10000
Точный	+ t₁	+ 0,1	+ 0,1	+ 0,2	+ 0,3	+ 0,4	+ 0,6	+ 1,0	—	—	—	—
— t₁	— 0,1	— 0,1	— 0,2	— 0,3	— 0,4	— 0,6	— 1,0	—	—	—	—
Средний	+ t₂	+ 0,2	+ 0,2	+ 0,4	+ 0,6	+ 1,0	+ 1,6	+ 2,4	+ 4	+ 6	+ 10	+ 16
— t₂	— 0,2	— 0,2	— 0,4	— 0,6	— 1,0	— 1,6	— 2,4	— 4	— 6	— 10	— 16
Грубый	+ t₃	+ 0,4	+ 0,6	+ 1,0	+ 1,6	+ 2,4	+ 4,0	+ 6,0	+ 8	+ 16	+ 24	+ 40
— t₃	— 0,4	— 0,6	— 1,0	— 1,6	— 2,4	— 4,0	— 6,0	— 8	— 16	— 24	— 40
Очень грубый	+ t₄	—	+ 1,0	+ 2,0	+ 3,0	+ 5,0	+ 8,0	+ 12,0	+ 16	+ 24	+ 40	+ 60
— t₄	—	— 1,0	— 2,0	— 3,0	— 5,0	— 8,0	— 12,0	— 16	— 24	— 40	— 60

А.3 Неуказанные предельные отклонения размеров притупленных кромок (наружных радиусов скругления и высот фасок) и угловых размеров для дополнительных вариантов должны соответствовать приведенным в таблицах и для соответствующих классов точности.

А.4 Ссылка на общие допуски с применением вариантов предельных отклонений линейных размеров, предусмотренных настоящим приложением, должна содержать номер настоящего стандарта и обозначения предельных отклонений согласно таблице . Примеры (для класса точности средний):

Вариант 1:

«Общие допуски по ГОСТ 30893.1: Н14, h14, ± t₂/2» или

«Общие допуски по ГОСТ 30893.1: Н14, h14, ± IТ14/2»

Вариант 2:

«Общие допуски по ГОСТ 30893.1: + t₂, — t₂, ± t₂/2»

Сочетание геометрических тел формирует деталь: руководство

Когда создается деталь, необходимо учесть сочетание различных геометрических тел, которые образуют ее форму. В данном руководстве мы рассмотрим основные виды сочетаний и объясним, как они влияют на конечный результат.

Первым и наиболее распространенным сочетанием геометрических тел является объединение. Оно используется, когда два или более тел сливаются в одно целое. Объединение может быть полным или частичным, в зависимости от требуемого результата. Например, при создании автомобильной кузовной части, сочетается множество панелей и других элементов для формирования окончательного вида.

Другим важным сочетанием является пересечение. Оно используется, когда необходимо объединить два или более тела в определенной точке или области. Пересечение может быть полным или частичным и может использоваться для создания отверстий или пазов на детали. Например, при проектировании деревянной мебели, сочетается несколько деревянных элементов, чтобы создать открытые полки или закрытые ящики.

Третьим видом сочетания является разность. Оно используется, когда одно тело вырезается или удалается из другого тела. Например, при создании кухонного ножа, лезвие формируется путем вырезания из металлического блока. Разность может быть полной или частичной, в зависимости от требований к детали.

Главное преимущество использования различных сочетаний геометрических тел заключается в создании сложных и уникальных форм, которые не могут быть достигнуты с использованием одного тела. Комбинирование различных геометрических форм позволяет достичь не только эстетической привлекательности детали, но и оптимальных функциональных характеристик.

При создании деталей формы, необходимо учитывать требования дизайна, прочности, удобства использования и других факторов. Комбинирование различных геометрических тел может быть сложным процессом, требующим точного планирования и выполнения. Однако, если правильно использовать эти сочетания, можно создать детали, уникальные по своему внешнему виду и функциональности.

В заключение, сочетание геометрических тел играет важную роль в формировании деталей. Знание различных видов сочетаний и их правильное применение помогут достичь желаемого результата и создать высококачественные изделия.

Понятие о допусках. Характеристика величин

Расчетные данные детали, поставляемые на чертеже, от которого производится отсчет отклонений, принято называть номинальным размером. Обычно эта величина выражается в целых миллиметрах. Размер детали, который фактически получается при обработке, называется действительным. Величины, между которыми колеблется этот параметр, принято называть предельным. Из них максимальный параметр — это наибольший предельный размер, а минимальный — наименьший. Отклонения — это разность между номинальной и предельной величиной детали. На чертежах этот параметр принято обозначать в числовой форме при номинальном размере (верхнее значение указывается выше, а нижнее — ниже).

Суммарные допуски формы и расположения

Каждый из этих параметров объединяет в себе оба допустимых отклонения. Они возникают в результате одновременного проявления изменения геометрической формы и появления неровности (шероховатости) обработанной поверхности. Поэтому используя математическую терминологию, говорят, что предел, к которому должна стремиться разница между эталоном и реальным изделием считается суммарным допуском формы и расположения. Характер изменений определяется методом сравнения с выбранными базовыми объектами. В качестве таких объектов выбирают проверенные конструкции или поверхностями, которые могут считаться эталонами, например, различные калибры.

Такие допуски делятся на следующие категории:

Биений. К ним относятся: радиальное, торцевое, в заранее заданном направлении;
Всей формы поверхности.

Каждый из этих категорий имеет свое обозначение. Допуск полного биения обозначается двумя наклонными стрелками в форме объединённых снизу векторов, направленных от левого нижнего угла в правый верхний. Сравнение форм производиться в результате совмещения обеих поверхностей.

Это поле имеет заданные геометрические размеры. Оно ориентировано относительно выбранной базы так, чтобы можно было проверить параллельность расположения. Примеры суммарного допуска обозначают, на сколько возможно изменение параметров, не приводящих к быстрому выходу из строя агрегата. Особенно это актуально для подвижных соединений