Вывод формулы момента инерции сплошного цилиндра

Примеры решения задач

ЗАДАЧА 1. Определить моменты инерции
плоского диска массы и радиуса  относительно осей,
перпендикулярных плоскости диска и проходящих через центр  и край диска .

РЕШЕНИЕ. Найдем сначала момент инерции . Поскольку масса диска распределена
непрерывно, воспользуемся формулой:

                                  (*)

В
качестве массы  выберем на диске
тонкое (толщиной ) кольцо радиуса , поскольку от любой его точки
до оси одинаковое расстояние . Если масса
диска  и его радиус , то масса единицы площади . Тогда масса нашего кольца: , где  — площадь выбранного кольца.
Подставим  — в интеграл (*):

.

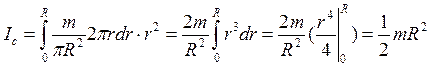Теперь
по теореме Штейнера, учитывая, что расстояние между осями , найдем

.

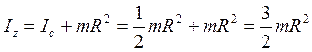ЗАДАЧА 2. В установке известны масса
однородного сплошного цилиндра , его радиус  и массы тел  и .
Скольжения нити и трения в оси блока нет. Найти зависимость от времени угловой
скорости цилиндра (если в момент времени  система
пришла в движение) и отношение натяжений  и
 вертикальных участков нитей в
процессе движения.

РЕШЕНИЕ. Расставим силы, действующие на тела  и ,
и запишем для их движения 2-ой закон Ньютона (направления ускорений указаны в
предположении, что тело  начало
опускаться). Тела  и  будут двигаться с одинаковыми
ускорениями, поскольку связаны нитью. Натяжения  и
 будут различны, поскольку
цилиндр весомый.

Спроектируем
эти уравнения на направления ускорений (для каждого тела эти направления свои):

Для вращающегося цилиндра запишем уравнение моментов: . На рисунке указаны силы, действующие на цилиндр и
направление вращения. Выберем ось ,
направленную перпендикулярно плоскости рисунка на нас, чтобы угловое ускорение
было положительным. По определению найдем моменты сил  и  относительно
точки О:  и  .
Их модули , ,
а направления указаны на рисунке. Моменты силы тяжести  и реакции опоры в оси  относительно точки О равны
нулю. Подставим проекции на ось  моментов сил
 и  в
уравнение моментов: . Момент инерции
сплошного цилиндра относительно собственной оси .
Поскольку скольжения нити по блоку нет, то ускорение нити () и ускорение точек, находящихся
на краю диска (), совпадают: . С учетом этого запишем систему
трех уравнений:

Поделим
последнее уравнение на  и сложим все три
уравнения:

.
Отсюда: . Поскольку угловое ускорение
постоянно и , то .

Теперь
из первых двух уравнений системы найдем  и
:

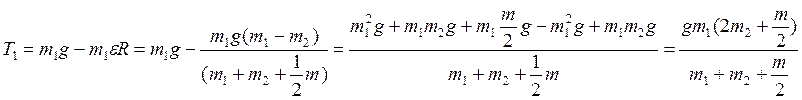
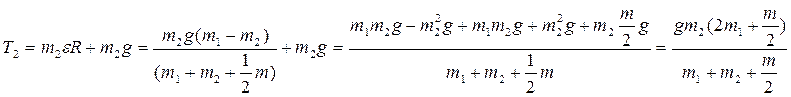Окончательно .

ЗАДАЧА 3. На горизонтальной
шероховатой поверхности лежит катушка ниток массы .
Ее момент инерции относительно собственной оси ,
где  — числовой коэффициент,  — внешний радиус катушки.
Радиус намотанного слоя ниток равен . Катушку без
скольжения начали тянуть за нить с постоянной силой ,
направленной под углом  к горизонту. Найти
модуль вектора ускорения оси катушки и работу силы  за
первые  секунд после начала движения.

Где используются знания величин I для цилиндров?

Пожалуй, основной областью применения изложенной выше теории является автомобильная промышленность. В частности, коленчатый вал автомобиля снабжен тяжелым сплошным маховиком, имеющим цилиндрическую форму. Необходим маховик для того, чтобы обеспечить максимальную плавность вращения коленчатого вала, что отражается на плавности автомобильного хода. Маховик гасит любые большие угловые ускорения как во время разгона транспортного средства, так при его торможении.

Из формулы выше для момента инерции I₁ понятно, что для увеличения этой величины выгоднее увеличить радиус, чем массу цилиндра (маховика). Так, удвоение массы приведет лишь к удвоению момента инерции. Однако если увеличить в два раза радиус, то I₁ возрастет аж в 4 раза, что обеспечит более эффективное использование маховика.

Что такое инерция?

Инерция в физике – способность тел определенное время сохранять состояние движения при отсутствии действия внешних сил. Впрочем, понятие инерции имеет частое применение не только в физике, но и в нашей повседневной жизни. Так обычно «инертным» называют человека, который совершенно не проявляет никакой инициативы, делают только то, что ему скажут другие, и делает это крайне медленно, без какого-либо энтузиазма. «Движется по инерции», – говорим мы, когда хотим подчеркнуть, что что-то делается без какого-либо смысла, а просто потому, что так было заведено когда-то или в силу наработанной годами привычки. И если с понятием инерции все более-менее понятно, благодаря таким вот житейским примерам, то термин «момент инерции» требует более детального пояснения, чем мы и займемся в нашей статье.

Вращательное движение тела

При изучении темы ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА вы научитесь решать простые задачи кинематики тела. В таких задачах вводятся векторные величины — угловая скорость

ПОСТАНОВКА ЗАДАЧИ. Твердое тело вращается вокруг неподвижной оси. Заданы некоторые кинематические характеристики движения тела и (или) кинематические характеристики движения точки этого тела. Найти остальные кинематические характеристики движения тела или точки.

Пусть тело вращается вокруг оси z. Кинематические характеристики движения тела:

• — угол поворота
• — угловая скорость
• — угловое ускорение

Кинематические характеристики точки на теле:

• — радиус траектории (расстояние до оси вращения) R:
• — скорость
• — ускорение

1. Записываем систему уравнений для всех величин, входящих в условие задачи. В зависимости от условия возможны три основных варианта решения. Гл.7.Вращательное движение тела

— Неизвестный закон вращения. Записываем систему двух уравнений для скорости

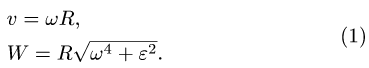
Для решения задачи необходимо, чтобы три из пяти величин

— Вращение с постоянной угловой скоростью. Интегрируя уравнение

Как правило, отсчет ведется от

— Вращение с постоянным угловым ускорением. Дважды интегрируя уравнение

получаем, при

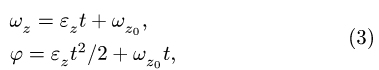
где

2. Решаем систему. Находим искомые величины.

Замечание. Ряд величин задан в тексте задач неявно. Например, угол поворота

Задача №5

Диск вращается вокруг неподвижной оси с постоянным угловым ускорением

1. В задаче задано постоянное угловое ускорение. Записываем систему уравнений для величин, входящих в условие задачи:

По условию задачи диск в начальный момент находился в покое, следовательно,

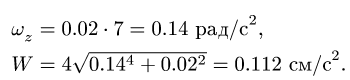
Ответ.

Передача вращения

Постановка Задачи. Механизм состоит из вращающихся на неподвижных осях блоков и поступательно движущихся элементов. Все элементы находятся во фрикционном, зубчатом или ременном зацеплениях. Задана какая-либо кинематическая характеристика одного из тел. Найти кинематические характеристики других тел.

1. Определяем кинематические характеристики тела, с заданным законом движения. Если это тело движется прямолинейно поступательно, то скорость и ускорение любой его точки имеет вид

где

где

2. Определяем угловую скорость тела, связанного нерастяжимой нитью (ремнем, тросом), фрикционно или зубчатым зацеплением с телом, угловая скорость которого известна:

где

в которое вместо радиусов

Если поступательное движение тела 1 передается вращательному движению тела 2 (или наоборот), то связь линейной и угловой скоростей имеет вид

где

3. Повторяя п.2 для всех пар кинематически связанных тел, составляем и решаем систему уравнений для неизвестных линейных и угловых скоростей.

4. Дифференцируя уравнения полученной системы, получаем аналогичную систему для угловых и линейных ускорений. Например, из уравнения (1) следует, что

Аналогично, из (2) следует связь линейного ускорения поступательно движущегося тела и углового ускорения связанного с ним вращающегося тела:

где

Задача №6

Механизм состоит из двух колес 1, 3 и блока 2, вращающихся на неподвижных осях. Ведущее колесо 1 механизма соединено ремнем с внутренним ободом блока 2. Внешний обод блока находится во фрикционном зацеплении с колесом 3 (рис. 84). Проскальзывание в точке зацепления отсутствует, ремень считать нерастяжимым.

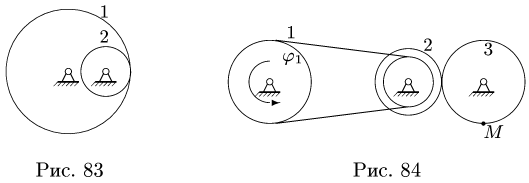
Задан закон движения ведущего колеса:

1. Находим угловую скорость ведущего колеса 1:

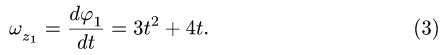
2. Определяем угловую скорость блока 2, связанного нерастяжимым ремнем с колесом 1:

где

3. Колеса 2 и 3 находятся во внешнем зацеплении и вращаются в разные стороны

Уравнения (3-5) образуют систему, решая которую, при t = 0.5 с, получаем

4. Дифференцируя уравнения системы (3-5), получаем аналогичную систему для угловых ускорений:

Решаем систему уравнений для ускорений (6) и получаем

Вычисляем ускорение точки М:

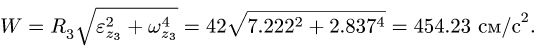
Ответ.

Рекомендую подробно изучить предмет:

Ещё лекции с примерами решения и объяснением:

• Равновесие тяжелой рамы
• Расчет составной конструкции
• Момент силы относительно оси
• Равновесие вала
• Неравномерное вращательное движение
• Плоскопараллельное движение тела
• Определение передаточных отношений различных передач
• Задачи на поступательное движение тела

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Осевые моменты инерции некоторых тел

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения

Материальная точка массы m

На расстоянии r от точки, неподвижная

Полый тонкостенный цилиндр или кольцо радиуса r и массы m

Сплошной цилиндр или диск радиуса r и массы m

Полый толстостенный цилиндр массы m с внешним радиусом r₂ и внутренним радиусом r₁

Сплошной цилиндр длины l, радиуса r и массы m

Ось перпендикулярна к цилиндру и проходит через его центр масс

Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m

Ось перпендикулярна к цилиндру и проходит через его центр масс

Прямой тонкий стержень длины l и массы m

Ось перпендикулярна к стержню и проходит через его центр масс

Тонкостенная сфера радиуса r и массы m

Ось проходит через центр сферы

Шар радиуса r и массы m

Ось проходит через центр шара

Конус радиуса r и массы m

Равнобедренный треугольник с высотой h, основанием a и массой m

Ось перпендикулярна плоскости треугольника и проходит через вершину

Правильный треугольник со стороной a и массой m

Ось перпендикулярна плоскости треугольника и проходит через центр масс

Квадрат со стороной a и массой m

Ось перпендикулярна плоскости квадрата и проходит через центр масс

Тонкостенный цилиндр (кольцо, обруч)

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

Толстостенный цилиндр (кольцо, обруч)

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

Момент инерции толстого кольца найдём как интеграл

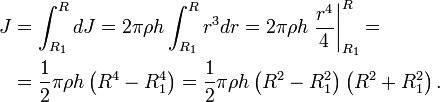
Поскольку объём и масса кольца равны

получаем окончательную формулу для момента инерции кольца

Однородный диск (сплошной цилиндр)

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят

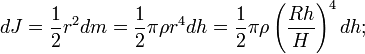
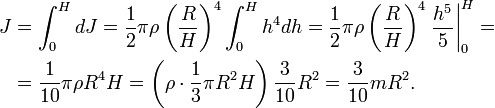
Сплошной однородный шар

Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

Масса и момент инерции такого диска составят

Момент инерции сферы найдём интегрированием:

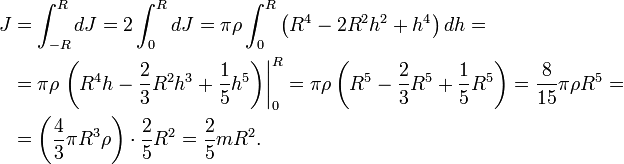
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

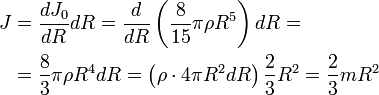
Тонкий стержень (ось проходит через центр)

Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

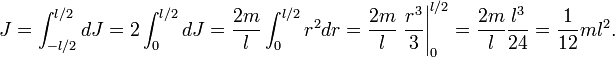
Тонкий стержень (ось проходит через конец)

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен

Вычисление моментов инерции

Моментом инерции материальной точки относительно оси называется число , где — масса точки, а — ее расстояние от оси. Аналогично определяется момент инерции относительно точки.

Пусть — материальная линия, линейная плотность которой во всех точках равна единице. Тогда масса элементарного участка этой линии равна его длине , а момент инерции такого участка относительно оси абсцисс равен . Интегрируя, получаем момент инерции относительно оси абсцисс всей линии:

. Так же доказывается, что и ,

где — момент инерции относительно начала координат. Отсюда следует, в частности, что .

Если линия задана параметрическими уравнениями , то

Аналогичные формулы справедливы для и

Моменты инерции криволинейной трапеции

Перейдем к вычислению моментов инерции криволинейной трапеции. Будем считать, что ее поверхностная плотность равна единице. Сначала найдем момент инерции прямоугольника со сторонами и относительно стороны .

Разобьем его на элементарные прямоугольники со сторонами и (см. рис. 61). Площадь (а потому и масса) каждого такого прямоугольника равна .

Значит, момент инерции элементарного прямоугольника относительно стороны равен , а момент инерции всего прямоугольника относительно этой стороны выражается формулой

Аналогично доказывается, что момент инерции криволинейной трапеции относительно оси ординат выражается формулой

(момент инерции элементарного прямоугольника относительно оси ординат равен ).

Полярный момент инерции (т. е. момент относительно начала координат) в этом случае выражается формулой

Пример 9. Вычислить момент инерции равнобедренного треугольника относительно его основания.

Решение. Расположим оси координат так, как показано на рисунке 65.

Пусть основание треугольника , высота . Прямая проходит через точки и . Ее уравнение , то есть .

Ясно, что момент инерции треугольника относительно оси равен удвоенному моменту инерции треугольника относительно той же оси. Значит,

Рекомендованная литература и полезные ссылки

• Тарг С. М. Момент инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 206—207. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
• Showman, Adam P.; Malhotra, Renu. The Galilean Satellites (англ.) // Science. — 1999. — Vol. 286, no. 5437. — P. 77—84. — DOI:10.1126/science.286.5437.77. — PMID 10506564.
• Margot, Jean-Luc; et al. Mercury’s moment of inertia from spin and gravity data (англ.) // Journal of Geophysical Research (англ.)русск. : journal. — 2012. — Vol. 117. — DOI:10.1029/2012JE004161.
• Галкин И.Н. Внеземная сейсмология. — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X.
• Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
• Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
• Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
• Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3

Эта статья доступна на английском языке – Moment of Inertia.

Схожі записи:

Геология и физика

Магнитострикция: эффект, умноженный многократно

Проверить алгебру гармонией: о связи науки и красоты

Самофокусировка мощных лучей

Температура по точкам

Вычисляем момент инерции протяженного объекта

Момент инерции легко вычисляется для очень маленького (точечного) объекта, если все точки объекта расположены на одинаковом расстоянии от точки вращения. Например в предыдущем примере, если считать, что мячик для игры в гольф гораздо меньше длины нити, то все его точки находятся на одинаковом расстоянии от точки вращения, равном радиусу окружности вращения ​\( r \)​. В таком случае момент инерции имеет знакомый вид:

где \( r \) — это расстояние, на котором сосредоточена вся масса мячика \( m \).

Однако такая идеальная ситуация имеет место далеко не всегда. А чему равен момент инерции протяженного объекта, например стержня, вращающегося относительно одного из своих концов? Ведь его масса сосредоточена не в одной точке, а распределена по всей длине. Вообще говоря, для определения момента инерции протяженного объекта нужно просуммировать моменты инерции всех материальных точек объекта:

Например, момент инерции ​\( l \)​ системы из двух “точечных” мячиков для игры в гольф с одинаковой массой ​\( m \)​ на расстояниях ​\( r_1 \)​ и ​\( r_2 \)​ равен сумме их отдельных моментов инерции ​\( l_1=mr_1^2 \)​ и \( l_2=mr_2^2 \):

А как определить момент инерции диска, вращающегося относительно своего центра? Нужно мысленно разбить диск на множество материальных точек, вычислить момент инерции каждой такой точки и просуммировать полученные моменты инерции. Физики научились вычислять моменты инерции для многих объектов со стандартной формой. Некоторые из них приведены в табл. 11.1.

Попробуем вычислить моменты инерции нескольких предметов с простой геометрией.

Пример: замедление вращения компакт-диска

Компакт-диски могут вращаться с разными угловыми скоростями. Это необходимо для обеспечения одинаковой линейной скорости считывания информации на участках, находящихся на разных расстояниях от центра вращения. Пусть диск массой 30 г и диаметром 12 см сначала вращается со скоростью 700 оборотов в секунду, а спустя 50 минут — со скоростью 200 оборотов в секунду. Какой средний момент сил действует на компакт-диск при таком уменьшении скорости? Связь момента сил и углового ускорения имеет вид:

Момент инерции диска с радиусом ​\( r \)​, вращающегося относительно своего центра в плоскости диска, выражается формулой:

Подставляя значения, получим:

Теперь нужно определить угловое ускорение, которое определяется следующей формулой:

Изменение угловой скорости ​\( \Delta\omega \)​ произошло за промежуток времени:

В данном примере изменение угловой скорости:

где ​\( \omega_1 \)​ — конечная, а \( \omega_0 \) — начальная угловая скорость компакт-диска.

Чему они равны? Начальная скорость 700 оборотов в секунду означает, что диск за секунду 700 раз проходит ​\( 2\pi \)​ радиан:

Аналогично, конечная скорость 200 оборотов в секунду означает, что диск за секунду 200 раз проходит \( 2\pi \) радиан:

Подставляя значения в формулу углового ускорения, получим:

Подставляя значения момента инерции и углового ускорения в итоговую формулу момента силы, получим:

Итак, средний момент равен 10-4 Н·м, а чему будет равна сила для создания такого момента, если она приложена к краю диска? Ее величину легко вычислить по следующей формуле:

Оказывается, для такого замедления компакт-диска нужно приложить не такую уж и большую силу.

Еще один пример: поднимаем груз

Вращательное движение порой внешне выглядит не так очевидно, как вращение ком- пакт-диска. Например подъем груза с помощью блока также является примером вращательного движения. Хотя канат и груз движутся поступательно, но сам блок вращается (рис. 11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.

В данном примере нужно вычислить сумму всех моментов сил ​\( \mathbf{\sum\! M} \)​, которые действуют на веревку:

В данном примере на веревку действует два момента сил: один ​\( M_1 \)​ со стороны груза весом ​\( mg \)​, а другой \( M_2 \) — со стороны горизонтальной силы ​\( F \)​:

Отсюда получаем формулу для углового ускорения:

Эти моменты ​\( M_1 \)​ и \( M_2 \) имеют одинаковое плечо, равное радиусу блока ​\( r \)​, поэтому:

Поскольку блок имеет форму диска, то из табл. 11.1 находим его момент инерции:

Подставляя выражения для ​\( l \)​, ​\( M_1 \)​ и ​\( M_2 \)​ в формулу для углового ускорения, получим:

Подставляя значения, получим:

Что такое момент инерции?

Момент инерции – это величина, отражающая степень инертности твердого тела относительно оси вращения. Она характеризует распределение массы тела относительно этой оси. Чем больше момент инерции, тем тяжелее вращать тело вокруг оси, и наоборот.

Момент инерции имеет важное значение в механике, так как позволяет рассчитывать эффективность вращательного движения твердого тела. Например, на основе момента инерции можно вычислить угловое ускорение, угловую скорость и кинетическую энергию тела при вращении

Формула для расчета момента инерции

Момент инерции зависит от различных параметров тела, включая форму, геометрические размеры и распределение массы. Для расчета момента инерции различных тел существуют специальные формулы.

Например, для расчета момента инерции сплошного цилиндра относительно его оси вращения применяется следующая формула:

I = m R2/2,

где m – масса цилинда, R – радиус цилиндра.

Момент инерции

Инерция проявляется не только для прямолинейного движения, но и при вращении тел. В двигателе есть специальное устройство – маховик (на рисунке справа маховик покрашен темно-серым цветом и имеет зубчики). Инерция его вращения помогает работать двигателю нормально. Энергия расширяющихся газов при воспламенении топлива толкает поршень вниз, а затем ему нужно идти вверх, выталкивая продукты сгорания. Без маховика поршень не смог бы провернуть коленвал без рывков. Двигатель без маховика заглохнет.

Ну а со спинерами и волчками знакомы многие.

Вот только в приведенных примерах форма тела не меняется. А изменится ли инертность тела при изменении его формы?

Вращение на фигурном катании

Многие могут вспомнить фигурное катание. Масса тела фигуриста за выступление не меняется. Но его скорость вращения мгновенно увеличивается, стоит прижать руки и ноги, и вытянуться в струнку. Т.е. при уменьшении радиуса тела скорость вращения увеличивается. Т.е. инертность тела должна уменьшиться? Давайте разбираться.

Вернемся к формулам. Скорость вращающегося тела описывается как произведение угловой скорости (омега) на радиус:

Скорость вращающегося тела

При этом кинетическая энергия вращающегося тела примет вид:

Синим цветом выделено произведение массы тела на радиус в квадрате. Эта величина называется моментом инерции вращающегося тела и обозначается латинской буквой I (и).

Мерой инертности вращающего тела выступает момент инерции, который зависит от массы тела и расстояния этой массы от центра вращения.

Представим, что девочка не только вращает груз над собой, но и идет. Тогда полная кинетическая энергия девочки с грузом примет вид:

Первая часть описывает кинетическую энергию двигающейся прямолинейно с некоторой скоростью девочки с грузом, а вторая – кинетическую энергию вращающегося груза. Полная кинетическая энергия — это сумма энергии прямолинейно движущегося тела и энергии вращающегося тела. Точно так же кинетическая энергия будет рассчитываться для движущегося по столу раскрученного волчка или съезжающего с наклонной плоскости цилиндра.

Так как вращающееся тело может иметь форму, отличную от точки или маленького шарика, то и формула момента инерции для более точных расчетов может принимать разный вид.

Некоторые формулы для расчета момента инерции для тел разной формы

Пример.

Цилиндры одинаковой массы (m1 = m2), но разного радиуса (r₁ < r₂), скатываются с горки высотой h. Какой цилиндр скатится быстрее? Какое из тел обладает меньшей инертностью?

Цилиндры одинаковой массы, но разного радиуса, скатываются с горки высотой h

В верхней точке кинетическая энергия обоих цилиндров будет равна нулю, так как скорость равна нулю. Потенциальная энергия будет одинаковой и максимальной.

Потенциальная и кинетическая энергия 1 и 2 цилиндра верхней точке

При скатывании цилиндров по закону сохранения энергии потенциальная энергия переходит в кинетическую и в самой нижней точке будет равна нулю, так как высота равна нулю. А кинетическая энергия в нижней точке будет складываться из поступательной кинетической энергии и кинетической энергии вращающегося тела и у обоих тел также будет одинаковой, так как их потенциальные энергии были равны.

Кинетическая энергия первого и второго цилиндра в нижней точке

Но так как радиус первого тела меньше второго, то и момент инерции первого тела меньше второго и будет справедливо:

Тогда для кинетической энергии поступательного движения будет справедливо отношение:

Следовательно, скорость первого цилиндра должна быть выше скорости второго, и он скатится быстрее. Так как мерой инертности вращающегося тела является момент инерции, то первое тело с меньшим радиусом и меньшим моментом инерции будет обладать меньшей инертностью, чем второе. Разогнаться под действием каких-либо сил (силы тяжести) такому телу проще.

Теорема Гюйгенса — Штейнера

Теорема была названа в честь двух математиков, давших формулировку определению характеристики параллельных осей. Например, пусть имеется объект произвольной формы, центробежная сила которого известна. Используя формулу Штейнера, можно вычислить момент тела относительно любой оси параллельной линии, проходящей через середину фигуры. В своём выводе учёные опирались на две формулы:

1. Вычисления координаты центра масс: X = (m1*x1 + m2*x2+…+Mi*Xi) / (m1+m2+…+Mi) = (Σ Δ mi*ri 2)/ m.
2. Универсального расчёта инерции любого тела: I = Σ Δ mi*ri 2.

Обозначив центр произвольной оси буквой O, а один из множества кусков — Δm, можно воспользоваться универсальной формулой. Сначала необходимо определить квадрат расстояния до оси вращения ri. Для этого через центр проведём ось Oц, а расстояние между O и Oц обозначим как d.

Указанные значения нужно выразить через координаты кусочка. Для этого строится ось абсциссы, проходящая через Oц, и ординаты — O. При таком выборе направления начала координат x центр масс равняется d, а у — нулю. Фактически получится прямоугольный треугольник. Воспользовавшись теоремой Пифагора, можно записать: I = Σ Δ mi* (xi2 + yi2).

В результате можно отметить, что момент в точке O будет прямо пропорционален расстоянию между Δ m и центром. Это и есть главный вектор на чертеже. Для его обозначения вводится длина r’.

Находится ri’2 по формулам для прямоугольного треугольника, в котором один катет равняется yi, а другой — xi — Oц. Значение ri’ совпадает с длиной гипотенузы. Таким образом, ri’2 = (xi — Oц)2 + yi2. Подставив полученное равенство в формулу нахождения параметра момента в центре, можно получить следующую формулу: Io = Σ Δ mi* ((xi — Oц)2 + yi2). После ряда подстановок и упрощения выражения в итоге получится равенство Io = I + m*x i2 — 2*m*xi2 = I — m*xi2.

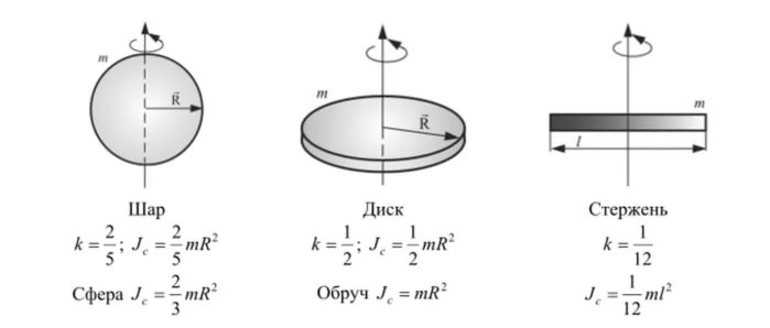
Так как x центра масс совпадает с d, расстоянием между осями, одну из которых можно направить через центр, то формулу можно переписать как Io = I — m*d2. Выразив из выражения произвольный момент, формула Штейнера примет вид I = Io + m*d2.

Другими словами, теорема определяет, что характеристика инерции тела относительно любой оси находится как сумма моментов относительно параллельной оси, пересекающей центр масс, и произведению массы тела на квадрат расстояния между осями. Сопротивлением вращению пренебрегают.

V. Вывод формулы для определения момента инерции.

hh₁h₂

При
опускании
нижнего диска
потенциальная энергия переходит в
кинетическую энергию вращательного
движения

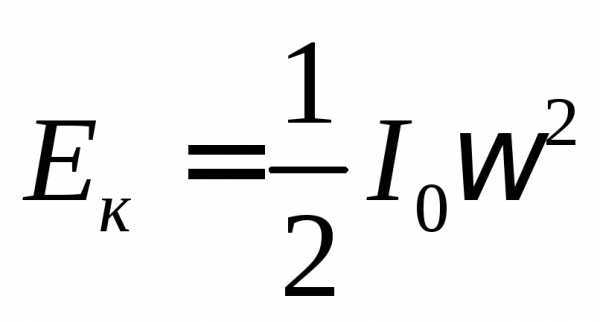
где I – момент инерции нижнего диска,  –
угловая скорость диска.

Вмомент прохождения диском поло­жения
равновесия угловая скорость,
а, следовательно, и кинетическая энергия,
принимает максимальное значение, т.е.



Если
пренебречь трением, то на основании
закона сохранения энер­гии для
колеблющегося диска можно записать:

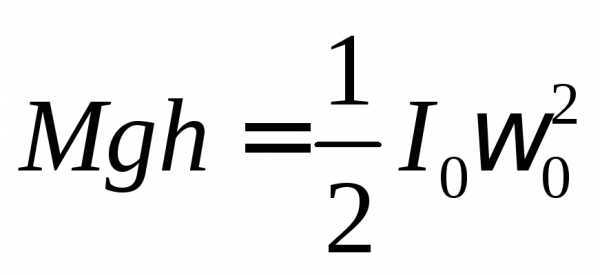
Угловая
скорость ,
являющаяся первой производной от
сме­щенияпо времени, может
быть записана

Максимальное
значение угловой скорости равно:

.
(3)

На
основании выражений (2) и (3) имеем:

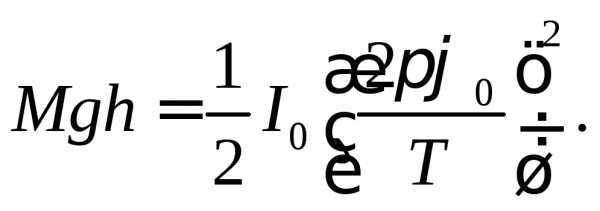
Найдем
величину hпри
повороте диска на малый угол ,
считая, что h₁ + h₂  2l:

.
(5)

Из
рис.1 ясно, что

и .

Подставляя
значение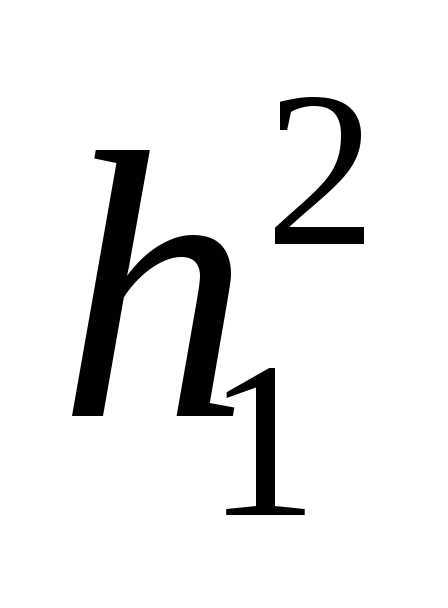

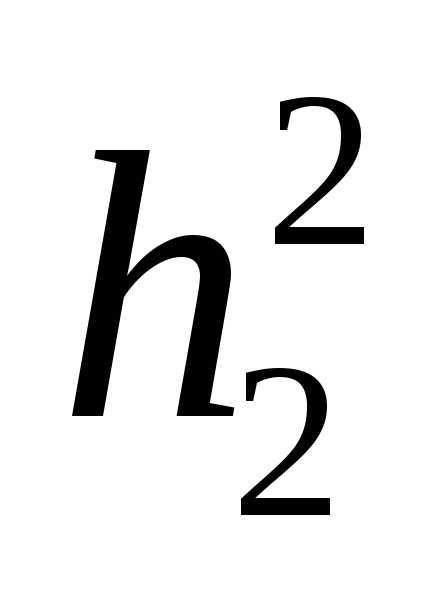
Вследствие
малости угла

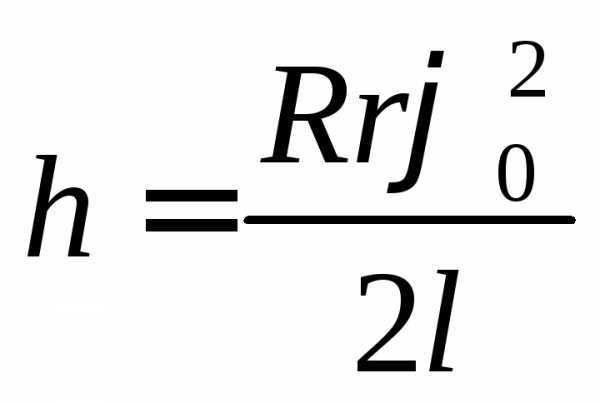
Подставив
выражения (3) и (6) в формулу (2), получим:

,
или

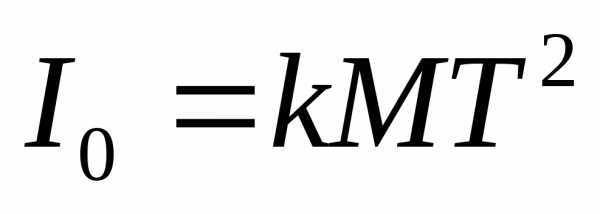
где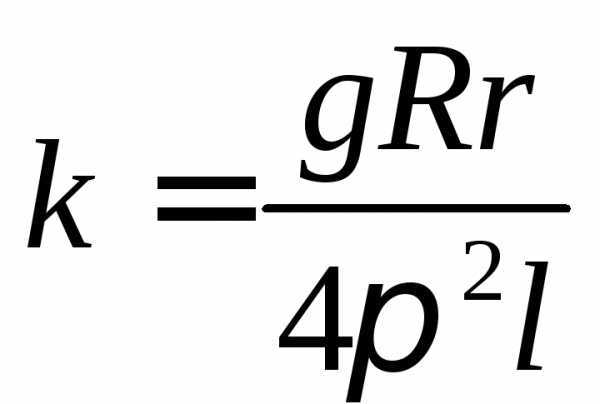

1. Определение момента инерции i0 диска без нагрузки.

а)
Заставить диск совершать крутильные
колебания с малой амплитудой (10 15 градусов). Секундомером измерить времяtсовершенияnполных колебаний (n– задаётся преподавателем). Все измерения
провести несколько раз. Все значения
занести в табл.1.

б)
Провести статистическую обработку
времени tпо
методу Стьюдента.

в)
Определить период колебаний диска Т =

tn

г)
Занести в табл.2 массу диска Ми постоянную установкиk.

д)
По формуле (7) рассчитать значение момента
инерции диска I,
результат занести в таблицу 2.

е)
Вычислить относительные и абсолютные
погрешности по формулам (8) – (9) и занести
результаты в таблицу 3.

(8)

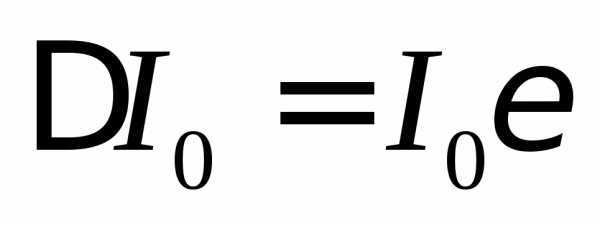
Абсолютная
погрешность периода колебаний определяется
следующим образом

Таблица
1

№/№ п/п	t	 t	t2	Sn	t(,n)	 tсл	 tпр	 t	n	T	T
с	с	с2	с	–	с	c	с	–	с	с
1
2
3
…
cреднее

Таблица
2

	k	M	m	d	I	I1	I2	I3
	м2с–2	кг	кг	м	кгм2	кгм2	кгм2	кгм2
Среднее значение
Абсолютная погрешность		510-4
Относительная погрешность