Толстостенный цилиндр (кольцо, обруч)
Сформулируйте основное уравнение динамики вращательного движения и дайте определение всем величинам, входящим в уравнение.
. (4.8)
Угловое ускорение, приобретаемое твердым телом, прямо пропорционально результирующему моменту всех действующих на тело внешних сил и обратно пропорционально моменту инерции тела.
Для описания вращательного движения твердого тела вводят понятие момента силы
. (4.6)
Мерой инертности тела при вращательном движении служит момент инерции J. Это скалярная величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний ri до оси вращения:
. (4.4)
В случае непрерывного распределения масс эта сумма сводится к интегралу:
,
быстрота изменения вектора угловой скорости характеризуется угловым ускорением :
Выведите рабочую формулу (4.15).
, (4.9)
где: а – ускорение падающего груза, r = d/2 – радиус шкива.
В свою очередь, пользуясь известным выражением для равноускоренного движения груза:
, (4.10)
( h – высота падения груза, t – время падения груза) находим:
, (4.11)
. (4.12)
Момент силы, приложенной к маятнику, находим по формуле (4.7), где: F – сила, действующая на шкив. Но
Силу F можно найти из уравнения движения груза:
, (4.13)
где: m – масса падающего груза, а
. (4.14)
Используя формулу (4.8) получим:
. (4.15)
3. Укажите основные источники погрешностей измерений. Выведите формулу для расчета погрешности J.
4. Какую роль играет момент инерции тела при его вращательном движении? Объясните физический смысл момента инерции.
Во вращательном движении большое значение имеет физическая величина, называемая моментом инерции тела. Эта величина играет такую же роль, как и масса при поступательном движении. Другими словами, момент инерции тела является мерой его инертности во вращательном движении, т.е. характеризует способность тела сохранять угловую скорость.
5. От чего зависит момент инерции маятника Обербека (формула (4.16))?
где: m = 0,114 кг – масса подвижного груза крестовины; R – расстояние от центра масс подвижного груза до оси вращения; r= 0,015 м – радиус груза; l = 0,02 м – длина образующей груза. Момент инерции системы без грузов J можно определить по формуле:
6.Выведите формулу для расчета момента инерции цилиндра или стержня.
Тонкостенный цилиндр (кольцо, обруч)
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
![]()
Момент инерции толстого кольца найдём как интеграл
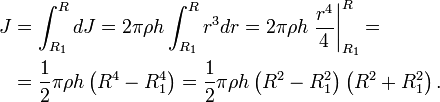
Поскольку объём и масса кольца равны
![]()
получаем окончательную формулу для момента инерции кольца
Тонкий стержень (ось проходит через центр)
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
![]()
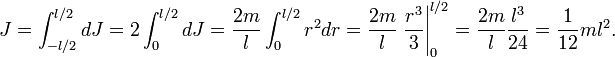
Тонкий стержень (ось проходит через конец)
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
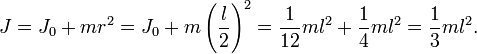
7. Сформулируйте теорему Штейнера и приведите примеры ее применения.
момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела JC относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
JC — известный момент инерции относительно оси, проходящей через центр масс тела,
J — искомый момент инерции относительно параллельной оси,
d — расстояние между указанными осями.
Как найти момент инерции
Чтобы немного упростить себе операции со всеми этими величинами перейдем к родной и понятной системе отсчета: перпендикулярным осям X и Y. Возьмем случайное сечение стержня и рассмотрим интегралы, как мы уже делали со статическими моментами:
Первые два интеграла называются осевыми моментами инерции относительно осей x и y, а третий — центробежным моментом инерции сечения относительно осей x, y. Теперь рассмотрим случай параллельного переноса осей , не вдаваясь глубоко в вычисление интегралов.
Для осей x1=x+a, y1=y+b моменты инерции будут равны:
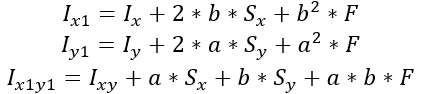
Если вы, как и часть прочитавших эту статью перед публикацией, не имеете черного пояса и седьмого дана в интегральных преобразованиях, то:
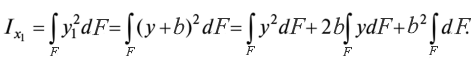
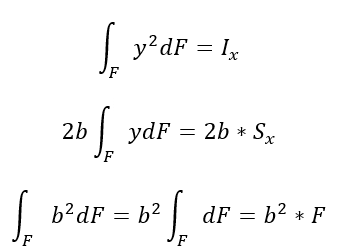
т.к.
и
Тут первый интеграл — Ix1, второй интеграл — Sx1, а третий раскрывается в площадь при нулевом свободном члене.
Надеюсь, понятно, что при параллельном переносе по y изменяется только ось (буква).
В последнем случае мы рассматриваем перенос по обеим осям сразу.
Где:Ix — очевидно, момент инерции относительно оси xSx — статический момент сечения относительно оси yF — площадь сечения
А теперь предположим, что некие оси x1 и y1 являются центральными, тогда и выражения упрощаются и принимают вид:
Немного проясню обозначение осей:
Центральными называются оси, проходящие через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю.
Главными называются оси, в которых центробежный момент инерции (Ixy) равен нулю. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения называются главными осями. Если эти оси являются также и центральными, то они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции.
И теперь можно уже коснуться практики: речь о моментах инерции простых сечений.
Момент инерции прямоугольника
Определим осевые моменты инерции прямоугольника со сторонами b и h относительно осей x и y, проходящих через его центр тяжести. В качестве элементарной площадки dA возьмем полоску шириной b и высотой . Тогда будем иметь:
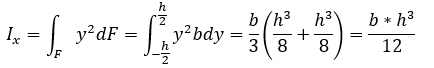
Не прибегая к вычислениям, замечу, что для момента инерции относительно оси Y изменится только положение сторон b и h. Следовательно:
Прямоугольник со сторонами b=h=a. Следовательно:
Момент инерции круга
Тут воспользуемся полярным моментом инерции относительно центра круга. Определим его, как сумму колец с толщиной dp:
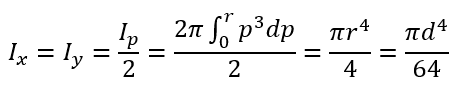
Момент инерции кольца
А здесь – явная аналогия с моментом инерции круга:
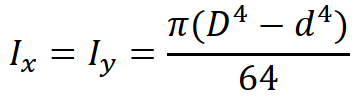
Как мы видим, момент инерции кольца это разность моментов инерции большего и меньшего кругов.
Тензор инерции и эллипсоид инерции
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
- (1),
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
- ,
.
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- ,
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
и произведя замены:
- ,
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
Инерция, кинетическая энергия, работа
Приведем другой пример. Представь тяжелоатлета… Даже двух, которые решили поставить мировой рекорд и сдвинуть самолет. Им придется приложить немало сил, чтобы вначале разогнать самолет от нуля до некоторой скорости, а потом поддерживать эту скорость, преодолевая силу трения, направленную назад. Конечно, проще сдвинуть с места (преодолеть инерцию покоя) и разогнать до большой скорости тело меньшей массы, например, футбольный мяч. Инертность самолета во много раз больше инертности футбольного мяча.
Силачи тянут Ил-76
А к какому трюку прибегает фокусник, чтобы в случае со скатертью все предметы остались на столе? Правильно, нужно выдернуть скатерть за наименьшее время. Чем меньше время, тем меньше энергии перейдет с силой трения на предметы и они просто не успеют разогнаться.
Трюк со скатертью
Энергия движущегося тела называется кинетической энергией и измеряется в Джоулях. Если тело неподвижно, кинетическая энергия равна нулю.
Чтобы разогнать тело массой m до нужной скорости V из состояния покоя (например, самолет), нужно выполнить работу, равную кинетической энергии разогнанного тела (без учета разных потерь):
Работа по изменению кинетической энергии тела совершается за счет приложения к нему некоторой силы – силы тяжести, силы трения, силы воздействия на него другого тела (тяжелоатлета-силача, дующего ветра, реактивной тяги ракетного двигателя и пр.).
Пусть силач разогнал до 0.1 м/с (10 сантиметров в секунду) легковую машину массой 1200 кг и самолет Ил-76 массой 88 500 кг в космосе (не будем учитывать силу трения). Тогда для преодоления инерции этих тел ему пришлось сжечь мышечной энергии на 6 Дж и 442,5 Дж соответсвенно. Т.е. на преодоление инерции покоя у самолета у спортсмена уйдет в 74 раза больше энергии, чем на автомобиль.
Чтобы остановить тело массой m, движущееся со скоростью V, нужно совершить обратную работу, равную отрицательному значению кинетической энергии этого тела:
Т.е. чем больше скорость тела и его масса, тем больше энергии на преодоление инерции движения надо затратить.
Если выключить мотор, машина под действием силы трения ее движущихся частей друг о друга, силы трения о воздух корпуса и силы трения колес об асфальт остановится сама. Но остановить машину можно и быстрее, увеличив силу трения с помощью тормозных дисков, т.е. выжав педаль тормоза.
При равной скорости масса грузовика намного больше, а значит больше его кинетическая энергия. Двигаясь накатом грузовик остановится дальше, чем легковой автомобиль – его инертность выше. Кстати, можно ли остановить грузовик быстрее легкового автомобиля и при каких условиях?
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Осевые моменты инерции некоторых тел
Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
Материальная точка массы m
На расстоянии r от точки, неподвижная
Полый тонкостенный цилиндр или кольцо радиуса r и массы m
Сплошной цилиндр или диск радиуса r и массы m
Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1
Сплошной цилиндр длины l, радиуса r и массы m
Ось перпендикулярна к цилиндру и проходит через его центр масс
Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m
Ось перпендикулярна к цилиндру и проходит через его центр масс
Прямой тонкий стержень длины l и массы m
Ось перпендикулярна к стержню и проходит через его центр масс
Тонкостенная сфера радиуса r и массы m
Ось проходит через центр сферы
Шар радиуса r и массы m
Ось проходит через центр шара
Конус радиуса r и массы m
Равнобедренный треугольник с высотой h, основанием a и массой m
Ось перпендикулярна плоскости треугольника и проходит через вершину
Правильный треугольник со стороной a и массой m
Ось перпендикулярна плоскости треугольника и проходит через центр масс
Квадрат со стороной a и массой m
Ось перпендикулярна плоскости квадрата и проходит через центр масс
Тонкостенный цилиндр (кольцо, обруч)
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Сплошной однородный шар
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
Тонкий стержень (ось проходит через центр)
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Тонкий стержень (ось проходит через конец)
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
Где используются знания величин I для цилиндров?
Пожалуй, основной областью применения изложенной выше теории является автомобильная промышленность. В частности, коленчатый вал автомобиля снабжен тяжелым сплошным маховиком, имеющим цилиндрическую форму. Необходим маховик для того, чтобы обеспечить максимальную плавность вращения коленчатого вала, что отражается на плавности автомобильного хода. Маховик гасит любые большие угловые ускорения как во время разгона транспортного средства, так при его торможении.

Из формулы выше для момента инерции I1 понятно, что для увеличения этой величины выгоднее увеличить радиус, чем массу цилиндра (маховика). Так, удвоение массы приведет лишь к удвоению момента инерции. Однако если увеличить в два раза радиус, то I1 возрастет аж в 4 раза, что обеспечит более эффективное использование маховика.
1 семестр МП / Экзамен 2 поток / Осевые моменты инерции некоторых тел
Осевые моменты инерции некоторых тел
Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
Материальная точка массы m
На расстоянии r от точки, неподвижная
Полый тонкостенный цилиндр или кольцо радиуса r и массы m
Сплошной цилиндр или диск радиуса r и массы m
Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1
Сплошной цилиндр длины l, радиуса r и массы m
Ось перпендикулярна к цилиндру и проходит через его центр масс
Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m
Ось перпендикулярна к цилиндру и проходит через его центр масс
Прямой тонкий стержень длины l и массы m
Ось перпендикулярна к стержню и проходит через его центр масс
Тонкостенная сфера радиуса r и массы m
Ось проходит через центр сферы
Ось проходит через центр шара
Конус радиуса r и массы m
Равнобедренный треугольник с высотой h, основанием a и массой m
Ось перпендикулярна плоскости треугольника и проходит через вершину
Правильный треугольник со стороной a и массой m
Ось перпендикулярна плоскости треугольника и проходит через центр масс
Квадрат со стороной a и массой m
Ось перпендикулярна плоскости квадрата и проходит через центр масс
Тонкостенный цилиндр (кольцо, обруч)
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
![]()
Момент инерции толстого кольца найдём как интеграл
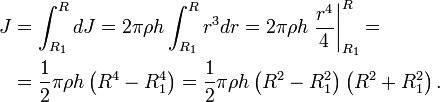
Поскольку объём и масса кольца равны
![]()
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
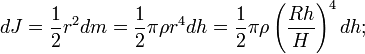
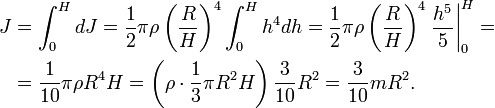
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
![]()
Момент инерции сферы найдём интегрированием:
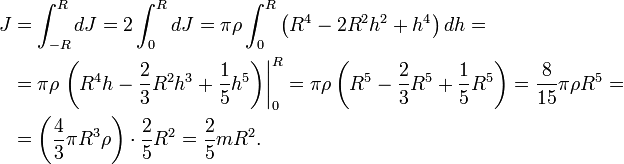
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
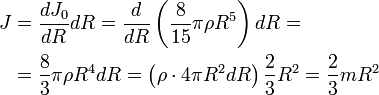
Тонкий стержень (ось проходит через центр)
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
![]()
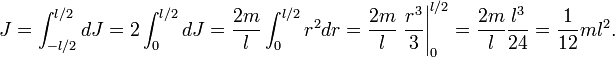
Тонкий стержень (ось проходит через конец)
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Что такое момент инерции?
Эту величину обычно обозначают буквой I. Для материальной точки математическая формула момента инерции записывается так:
Где r — расстояние до оси вращения от точки массой m. Из формулы понятно, что единицей измерения величины являются килограммы на квадратный метр (кг*м 2 ).
Если тело имеет сложную форму и его объемная плотность является переменной, тогда для определения I следует использовать такое интегральное выражение:
Где dm — это элементарная масса, находящаяся от оси вращения на расстоянии r.
Таким образом, момент инерции определяет распределение материи в теле сложной формы относительно конкретной оси вращения системы.
Вращательное движение тела
При изучении темы ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА вы научитесь решать простые задачи кинематики тела. В таких задачах вводятся векторные величины — угловая скорость
ПОСТАНОВКА ЗАДАЧИ. Твердое тело вращается вокруг неподвижной оси. Заданы некоторые кинематические характеристики движения тела и (или) кинематические характеристики движения точки этого тела. Найти остальные кинематические характеристики движения тела или точки.
Пусть тело вращается вокруг оси z. Кинематические характеристики движения тела:
- — угол поворота
- — угловая скорость
- — угловое ускорение
Кинематические характеристики точки на теле:
- — радиус траектории (расстояние до оси вращения) R:
- — скорость
- — ускорение
1. Записываем систему уравнений для всех величин, входящих в условие задачи. В зависимости от условия возможны три основных варианта решения. Гл.7.Вращательное движение тела
— Неизвестный закон вращения. Записываем систему двух уравнений для скорости
Для решения задачи необходимо, чтобы три из пяти величин
— Вращение с постоянной угловой скоростью. Интегрируя уравнение
Как правило, отсчет ведется от
— Вращение с постоянным угловым ускорением. Дважды интегрируя уравнение
получаем, при
где
2. Решаем систему. Находим искомые величины.
Замечание. Ряд величин задан в тексте задач неявно. Например, угол поворота
Задача №5
Диск вращается вокруг неподвижной оси с постоянным угловым ускорением
1. В задаче задано постоянное угловое ускорение. Записываем систему уравнений для величин, входящих в условие задачи:
По условию задачи диск в начальный момент находился в покое, следовательно,
Ответ.
Передача вращения
Постановка Задачи. Механизм состоит из вращающихся на неподвижных осях блоков и поступательно движущихся элементов. Все элементы находятся во фрикционном, зубчатом или ременном зацеплениях. Задана какая-либо кинематическая характеристика одного из тел. Найти кинематические характеристики других тел.
1. Определяем кинематические характеристики тела, с заданным законом движения. Если это тело движется прямолинейно поступательно, то скорость и ускорение любой его точки имеет вид
где
где
2. Определяем угловую скорость тела, связанного нерастяжимой нитью (ремнем, тросом), фрикционно или зубчатым зацеплением с телом, угловая скорость которого известна:
где
в которое вместо радиусов
Если поступательное движение тела 1 передается вращательному движению тела 2 (или наоборот), то связь линейной и угловой скоростей имеет вид
где
3. Повторяя п.2 для всех пар кинематически связанных тел, составляем и решаем систему уравнений для неизвестных линейных и угловых скоростей.
4. Дифференцируя уравнения полученной системы, получаем аналогичную систему для угловых и линейных ускорений. Например, из уравнения (1) следует, что
Аналогично, из (2) следует связь линейного ускорения поступательно движущегося тела и углового ускорения связанного с ним вращающегося тела:
где
Задача №6
Механизм состоит из двух колес 1, 3 и блока 2, вращающихся на неподвижных осях. Ведущее колесо 1 механизма соединено ремнем с внутренним ободом блока 2. Внешний обод блока находится во фрикционном зацеплении с колесом 3 (рис. 84). Проскальзывание в точке зацепления отсутствует, ремень считать нерастяжимым.
Задан закон движения ведущего колеса:
1. Находим угловую скорость ведущего колеса 1:
2. Определяем угловую скорость блока 2, связанного нерастяжимым ремнем с колесом 1:
где
3. Колеса 2 и 3 находятся во внешнем зацеплении и вращаются в разные стороны
Уравнения (3-5) образуют систему, решая которую, при t = 0.5 с, получаем
4. Дифференцируя уравнения системы (3-5), получаем аналогичную систему для угловых ускорений:
Решаем систему уравнений для ускорений (6) и получаем
Вычисляем ускорение точки М:
Ответ.
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Равновесие тяжелой рамы
- Расчет составной конструкции
- Момент силы относительно оси
- Равновесие вала
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Определение передаточных отношений различных передач
- Задачи на поступательное движение тела
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Момент инерции полого цилиндра
Теперь оставим ось на том же месте и найдем значение I для цилиндра с пустотой внутри (втулка, труба). Такую фигуру описывают двумя радиусами: внешним R1 и внутренним R2. В этом случае для интегрирования применяется абсолютно тот же подход, что и для сплошного цилиндра, только пределы теперь изменяются от R2 до R1. Имеем:
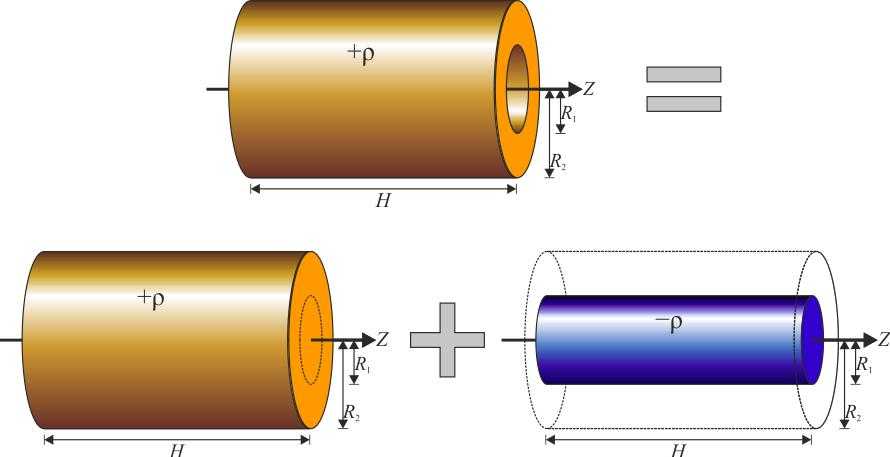
Для дальнейшего упрощения этой формулы воспользуемся разложением на множители выражения в скобках, получим:
Часть этого выражения вместе с первыми скобками является массой полого цилиндра, поэтому получаем конечную формулу:
Отсюда видно, что момент инерции полого цилиндра больше этого значения для сплошного цилиндра аналогичной массы и такого же внешнего радиуса на величину m*R2 2 /2. Этот результат не вызывает удивления, поскольку в полом цилиндре центр масс находится от оси вращения дальше, чем в сплошном.

Геометрический момент инерции
Геометрический момент инерции — геометрическая характеристика сечения вида
где — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.
Единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см4.
Из него выражается момент сопротивления сечения:
- .
| Геометрические моменты инерции некоторых фигур | |
|---|---|
| Прямоугольника высотой и шириной : | |
| Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно | |
| Круга диаметром |
Рекомендованная литература и полезные ссылки
- Тарг С. М. Момент инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 206—207. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- Showman, Adam P.; Malhotra, Renu. The Galilean Satellites (англ.) // Science. — 1999. — Vol. 286, no. 5437. — P. 77—84. — DOI:10.1126/science.286.5437.77. — PMID 10506564.
- Margot, Jean-Luc; et al. Mercury’s moment of inertia from spin and gravity data (англ.) // Journal of Geophysical Research (англ.)русск. : journal. — 2012. — Vol. 117. — DOI:10.1029/2012JE004161.
- Галкин И.Н. Внеземная сейсмология. — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X.
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
Эта статья доступна на английском языке – Moment of Inertia.
Схожі записи:
Геология и физика
Магнитострикция: эффект, умноженный многократно
Проверить алгебру гармонией: о связи науки и красоты
Самофокусировка мощных лучей
Температура по точкам
Литература
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А.Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с.
- Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Что такое момент инерции?
Момент инерции – это величина, отражающая степень инертности твердого тела относительно оси вращения. Она характеризует распределение массы тела относительно этой оси. Чем больше момент инерции, тем тяжелее вращать тело вокруг оси, и наоборот.
Момент инерции имеет важное значение в механике, так как позволяет рассчитывать эффективность вращательного движения твердого тела. Например, на основе момента инерции можно вычислить угловое ускорение, угловую скорость и кинетическую энергию тела при вращении
Формула для расчета момента инерции
Момент инерции зависит от различных параметров тела, включая форму, геометрические размеры и распределение массы. Для расчета момента инерции различных тел существуют специальные формулы.
Например, для расчета момента инерции сплошного цилиндра относительно его оси вращения применяется следующая формула:
I = m R2/2,
где m – масса цилинда, R – радиус цилиндра.































