Как построить цилиндр в трех плоскостях

Находим недостающие проекции точек на комплексных чертежах цилиндра и конуса

Ассоциативные чертежи в «Инженерной графике» называют комплексными.

Как найти недостающие проекции точек на комплексном чертеже цилиндра?

находим недостающие проекции точки m цилиндре

Построение недостающих проекций точек на цилиндре аналогично нахождению их на призме. Принцип тот же, только вместо граней, здесь окружность.  Для нашего цилиндра недостающие проекции точек К и М находятся, как показано на рисунке при помощи вертикальных и горизонтальных линий связи.

Подробнее о процессе построения смотрите на уроке как найти проекции точек на пирамиде и призме

Как найти недостающие проекции точек на комплексном чертеже конуса?

находим проекции точек на конусе

Необходимо построить недостающие проекции точек К и М на комплексном чертеже конуса.

Точка М задана фронтальной проекцией m’, точка К – горизонтальной проекцией k.

построения при нахождении горизонтальной проекции точки

Построим горизонтальную проекцию m. Для этого:

1. через точку m’ и вершину конуса s проводим вспомогательную прямую до пересечения ее с основанием в точке a.
2. Затем через полученную точку а проводим вертикальную  линию связи до пересечения с окружностью основания конуса в точке b.
3. Через полученную точку b и вершину конуса s проводим прямую.
4. Опускаем вертикальную линию связи из точки m’ до пересечения с прямой bs.
5. Горизонтальная проекция m найдена.

Профильная проекция m’’ находится обычным образом по линиям связи.

Фронтальная проекция (k’) находится таким же, вышеописанным образом. Вот рисунок

строим фронтальную проекцию точки k

Профильную проекцию (k’’) находим по линиям связи.

Окончательно комплексные чертежи цилиндра и конуса выглядят так.

готовый комплексный чертеж конуса

готовый комплексный чертеж цилиндра

Для лучшего понимания материала рекомендую посмотреть видеоурок.

Презентация по черчению тема «Построение изометрической проекции куба» 9 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах

Изометрическое построение куба Составитель: учитель черчения Ячменев Иван Петрович МБОУ Олонская СОШ

Краткое описание документа:

Презентация составлена для урока черчения по теме «Построение аксонометрических проекций»

9 класс учебник черчение автор А.Д. Ботвинников.

Визуальная пошаговая инструкция (какие и как применяются инструменты) для построения

прямоугольной изометрической проекции куба с помощью циркуля.

Презентация создана для визуального восприятия умения построения чертежа.

Ищем педагогов в команду «Инфоурок»

Добавляем детали

После создания основной формы цилиндра, можно приступить к добавлению деталей и улучшению его внешнего вида. Вот несколько идей, которые помогут сделать ваш цилиндр более интересным и реалистичным:

• Добавьте болты: изобразите болты, которые крепят детали цилиндра. Вы можете использовать маленькие круглые фигуры, размещенные на поверхности цилиндра.
• Создайте текстуру: добавьте текстуры на поверхность цилиндра, чтобы он выглядел более реалистичным. Например, вы можете использовать текстуру металла или дерева.
• Улучшите освещение: добавьте эффект освещения, чтобы создать более реалистичную 3D-иллюзию. Используйте свет и тени, чтобы подчеркнуть форму и объем цилиндра.
• Добавьте декоративные элементы: вы можете добавить декоративные элементы, такие как ручки, кнопки или узоры на поверхности цилиндра, чтобы придать ему уникальный стиль.

Эти идеи помогут вам добавить детали к вашему цилиндру и сделать его более интересным и реалистичным. Используйте свою фантазию и экспериментируйте с различными элементами, чтобы создать уникальный дизайн цилиндра.

Проекции конусов

Нагляднее изображение прямого кругового ко­нуса показано на рис. 167, а. Боковая поверхность конуса получена вращением отрезка BS вокруг оси, пересекающей отрезок в точке S. Последова­тельность построения двух проекций конуса пока­зана на рис. 167, б и в. Сначала строят две проекции основания. Горизонтальная проекция основа­ния — окружность. Фронтальной проекцией будет отрезок горизонтальной прямой, равный диаметру этой окружности (рис. 167, б). На фронтальной проекции из середины основания восставляют перпендикуляр и на нем откладывают высоту конуса (рис. 167, в). Полученную фронтальную проекцию вершины конуса соединяют прямыми с концами фронтальной проекции основания и по­лучают фронтальную проекцию конуса.

Рис. 167

Если на поверхности конуса задана одна проек­ция точки А (например, фронтальная проекция на рис. 168, а). то две другие проекции этой точки определяют с помощью вспомогательных линий — образующей, расположенной на поверхности ко­нуса и проведенной через точку А, или окружнос­ти, расположенной в плоскости, параллельной основанию конуса.

В первом случае (рис 168. а) проводят фрон­тальную проекцию s’a’f ’ вспомогательной обра­зующей. Пользуясь вертикальной линией связи, проведенной из точки f, расположенной на фрон­тальной проекции окружности основания, находят горизонтальную проекцию sf этой образующей, на которой с помощью линии связи, проходящей через а’, находят искомую точку а.

Во втором случае (рис. 168. б) вспомогательной линией, проходящей через точку А, будет окруж­ность. расположенная на конической поверхности и параллельная плоскости Н. Фронтальная проек­ция этой окружности изображается в виде отрезка Ь’с’ горизонтальной прямой, величина которого равна диаметру вспомогательной окружности. Искомая горизонтальная проекция а точки А на­ходится на пересечении линии связи, опущенной из точки а’, с горизонтальной проекцией вспомо­гательной окружности.

Если заданная фронтальная проекция Ь’ точки В расположена на контурной (очерко­вой) образующей SK, то горизонтальная проекция точки находится без вспомогательных линий (рис. 168. б).

В изометрической проекции точку А, находя­щуюся на поверхности конуса, строят по трем координатам (рис. 168, в): x_А = n, y_А = m, z_А = h. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям. В рассматриваемом примере от точки О по оси х отложена координата x_А = n; из конца ее параллельно оси у проведена прямая, на которой отложена координата y_А = m; из конца отрезка, равного т, параллельно оси z проведена прямая, на которой отложена координата z_А = h. В резуль­тате построений получим искомую точку А.

Рис. 168

Проекции цилиндров

Боковая поверхность прямого кругового цилин­дра получается вращением отрезка АВ образую­щей вокруг оси, параллельной этому отрезку. На рис. 165, а представлена изометрическая проекция цилиндра.

Построение горизонтальной и фронтальной проекций цилиндра показано на рис. 165, б и в.

Построение начинают с изображения основания цилиндра, т.е. двух проекций окружности (рис. 165, б). Так как окружность расположена на плоскости Н, то она проецируется на эту плос­кость без искажения. Фронтальная проекция ок­ружности представляет собой отрезок горизон­тальной прямой линии, равный диаметру окруж­ности основания.

После построения основания на фронтальной проекции проводят две очерковые (крайние) обра­зующие и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, кото­рый является фронтальной проекцией верхнего основания цилиндра (рис. 165, в).

Рис. 165

Определение недостающих проекции точек А и В, расположенных на поверхности цилиндра, по заданным фронтальным проекциям в данном слу­чае затруднений нс вызывает, так как вся горизонтальная проекция боковой поверхности цилиндра представляет собой окружность (рис. 166. а). Следовательно, горизонтальные проекции точек А и В можно найти, проводя из данных точек а’ и b’ вертикальные линии связи до их пересечения с окружностью в искомых точ­ках а и Ь.

Профильные проекции точек А и В строят так­же с помощью вертикальных и горизонтальных линий связи.

Изометрическую проекцию цилиндра вычерчи­вают, как показано на рис. 166, б.

В изометрии точки A и В строят по координа­там. Например, для построения точки В от начала координат О по оси х откладывают координату x_B = n, а затем через ее конец проводят прямую, параллельную оси у, до пересечения с контуром основания в точке 1. Из этой точки параллельно оси x проводят прямую, на которой откладывают координату x_B = h₁ точки В.

Рис. 166

Финишные штрихи и финальная обработка:

Когда вы уже построили все необходимые линии и добавили детали, пришло время для финишных штрихов и финальной обработки вашего цилиндра в изометрии.

Во-первых, убедитесь, что все линии и углы ровные и четкие. Используйте линейку и уровень, чтобы проверить, что все линии горизонтальные, вертикальные и параллельные друг другу. Если вы обнаружите неровности, исправьте их, удаляя и рисуя линии повторно.

Затем вы можете приступить к добавлению дополнительных деталей, таких как ручки, кнопки или любые другие элементы, которые вы хотите добавить к вашему цилиндру. Используйте эскизы или фотографии в качестве образцов при необходимости.

Когда вы закончите добавлять детали, можете начать заливку цветом. Выберите подходящую краску или маркеры и аккуратно раскрасьте ваш цилиндр. Не забывайте использовать разные оттенки или цвета, чтобы сделать ваш цилиндр более интересным и реалистичным.

Наконец, проведите финальную обработку вашего проекта. Удалите все ненужные линии и конструкционные элементы, чтобы визуализировать чистый и готовый цилиндр. Проверьте всю работу на предмет ошибок или несоответствий и внесите необходимые правки.

Теперь ваш цилиндр в изометрии готов! Поздравляю, вы только что создали свой первый трехмерный объект! Наслаждайтесь результатом своей работы и продолжайте практиковаться, чтобы стать еще лучше в изометрическом рисовании.

Создание основы цилиндра:

1. Возьмите кусок картонной трубки или создайте основу из картона, оформив его в форму прямоугольника со сторонами, соответствующими длине и ширине будущего цилиндра.

2. С помощью ножниц или ножа аккуратно вырежьте прямоугольник из картона.

3. Следующим шагом является склеивание концов прямоугольника в кольцо. Используйте клей или скотч для надежного соединения сторон. Убедитесь, что кольцо получилось плотным и не имеет промежутков.

4. Проверьте, что кольцо стоит ровно на плоской поверхности и не покатится.

5. Определите диаметр кольца. Используйте линейку или мерную ленту и измерьте расстояние от одного края кольца до противоположного края, проходящего через центр. Запишите это значение.

6. Используя измеренный диаметр, найдите радиус кольца. Разделите значение диаметра пополам и запишите результат.

7. Возьмите новый кусок картонной трубки или создайте новый круглый основу из картона с использованием радиуса, которого вы только что нашли.

8. Отметьте центр нового круга и вырежьте его, чтобы получить цилиндрическую форму.

9. Убедитесь, что круг стоит ровно на плоской поверхности и не покатится.

10. Основа цилиндра готова и может быть использована для дальнейшей работы.

Шаг 1: Построение осей координат

Перед тем, как начать строить аксонометрическую проекцию цилиндра, необходимо построить оси координат. Эти оси будут помогать нам определить положение и направление цилиндра на плоскости.

Для этого проведите две пересекающиеся линии, которые будут служить основными осями координат. Оси должны быть перпендикулярными друг к другу. Например, проведите вертикальную ось, которая будет проходить через центр цилиндра, и горизонтальную ось, которая будет пересекать вертикальную ось в некоторой точке. Оси координат должны быть достаточно длинными, чтобы их можно было легко видеть.

На основе этих осей можно определить положение и направление цилиндра в пространстве. Ось, пересекающая цилиндр, будет определять его высоту, ось, параллельная цилиндру, будет определять его радиус.

Убедитесь, что оси координат ясно видны и легко идентифицируются. Отметьте точки пересечения осей (например, точку центра цилиндра) для использования при построении самого цилиндра в следующем шаге.

Начертание основного контура

Для начала нарисуйте прямоугольник, который будет служить основой для цилиндра. Для этого нарисуйте параллельные вертикальные линии вдали друг от друга на некотором расстоянии. Затем нарисуйте две горизонтальные линии, соединяющие верхние концы вертикальных линий и две горизонтальные линии, соединяющие нижние концы вертикальных линий.

После этого нарисуйте овал, который будет служить внешним контуром верхней крышки цилиндра. Чтобы построить овал, используйте две дуги, соединяющие левые верхний и правый верхний углы прямоугольника.

Затем начертите внутренний контур верхней крышки цилиндра. Для этого нарисуйте другой овал внутри первого овала, но на некотором расстоянии от его краев.

Чтобы закончить набросок, соедините все вертикальные линии, начерченные в начале, прямыми линиями к верхнему и нижнему контуру крышки цилиндра.

Шаг 2: Построение основных линий и форм цилиндра

После того, как вы определились с позицией цилиндра на плоскости и нарисовали основную форму, перейдите к построению основных линий цилиндра.

1. Для начала, проведите вертикальную линию в середине фигуры, которая будет служить осью цилиндра.

2. Затем, на верхушке этой оси проведите маленькую горизонтальную линию, которая будет выступать в качестве круга линии максимального диаметра цилиндра.

3. Соедините концы линии круга с верхними углами основной формы цилиндра, проведя дуги, чтобы создать овальную форму верхней части цилиндра.

4. Под осью цилиндра, проведите горизонтальную линию, чтобы создать нижнюю основу цилиндра.

5. Проведите дуги, соединяющие нижние углы основной формы с концами линии нижней основы, чтобы закрыть форму цилиндра.

6. Подсоедините к двум боковым частям основной формы цилиндра линию, чтобы создать боковую поверхность цилиндра. Эта линия должна быть параллельна оси цилиндра.

После выполнения всех этих шагов, вы должны получить основные линии и формы для цилиндра в изометрии. Теперь можно приступать к добавлению деталей и отделки, чтобы придать цилиндру более реалистичный вид.

Добавление деталей и декоративных элементов:

Здесь не ограничивайте свою фантазию! Вы можете использовать различные формы и размеры элементов, чтобы придать своему цилиндру уникальный вид.

Однако не забывайте о сбалансированности и гармонии деталей. Попробуйте не перегружать цилиндр слишком многими элементами, чтобы не засорить его общий вид.

Вы также можете использовать различные методы для создания деталей. Например, вы можете добавить элементы с помощью отдельных полигонов или использовать текстуры и накладывать их на модель. Экспериментируйте и находите свой собственный стиль!

Не забудьте также учесть перспективу и изометрическую проекцию при создании деталей. Вам может потребоваться немного экспериментировать, чтобы найти правильные пропорции и углы.

По завершении этапа добавления деталей и декоративных элементов, ваш цилиндр будет готов к рендерингу и использованию в вашем проекте. Получившийся объект может быть использован в играх, архитектурных визуализациях, анимациях и многих других сферах.

Удачи в создании вашего цилиндра в изометрии!

Шаг 3: Создание объема

Теперь наш цилиндр обретает объем и становится более реалистичным. Для этого нам потребуется нарисовать эллипс на основе овала, который мы создали на предыдущем шаге.

1. Установите кисть таким образом, чтобы она была округлой и мягкой. Затем выберите светлый оттенок для цвета эллипса.

2. Нарисуйте эллипс на верхней части овала, придавая ему выпуклую форму. Не забудьте остановиться, когда достигнете конца овала.

3. Вернитесь к деталям эллипса и добавьте небольшие штрихи и тени, чтобы придать цилиндру рельефность.

Теперь наш цилиндр выглядит более объемным и реалистичным. В следующем шаге мы добавим детали и отделку, чтобы сделать его полноценным объектом в изометрической перспективе.

Проекции шара

На рис. 169, а изображена половина шара, сферическая поверхность этого шара образована вращением четверти окружности АВ вокруг ради­уса АО.

Проекции этой фигуры приведены на рис. 169, б. Горизонтальная проекция — окруж­ность радиуса, равного радиусу сферы, а фрон­тальная — полуокружность того же радиуса.

Если точка А расположена на сферической поверхности (рис. 169, в), то вспомогательная линия Ь’с’, проведенная через эту точку параллельно горизонтальной плоскости проекций, прое­цируется на горизонтальную плоскость проекций окружностью. На горизонтальной проекции вспо­могательной окружности находят с помощью ли­нии связи искомую горизонтальную проекцию а точки А.

Величина диаметра вспомогательной окружнос­ти равна фронтальной проекции Ь’с’.

Рис. 169

Шаг 1: Понимание основных принципов изометрической графики

Понимание основных принципов изометрической графики поможет вам нарисовать цилиндр и другие объекты с правильной перспективой. Основные принципы изометрической графики включают:

• Изометрическая ось — это ось, которая идет под углом 30 градусов к горизонтали.
• Изометрическая сетка — это регулярная сетка из равноотстоящих горизонтальных и вертикальных линий, которые проходят через изометрическую ось.
• Угол изометрической оси — это угол, который определяет направление горизонтальных и вертикальных линий на изометрической сетке. Обычно угол изометрической оси составляет 120 градусов.

Теперь, когда вы понимаете основные принципы изометрической графики, вы готовы приступить к рисованию цилиндра. Продолжайте чтение, чтобы узнать, как это сделать!

Что необходимо для рисования цилиндров

Рисование цилиндра в изометрии может быть увлекательным и творческим занятием, но для этого вам понадобятся определенные инструменты и материалы:

1. Лист бумаги или холст, на котором будете рисовать. Изометрическая бумага может быть очень полезной, так как на ней уже нарисованы сетки, которые помогут соблюсти пропорции и углы при рисовании.

2. Карандаши и ручки. Обычные графитовые карандаши позволяют рисовать легко стирающиеся линии, а цветные карандаши и ручки добавят яркие оттенки и насыщенность к вашему рисунку.

3. Линейка и компас. Они помогут нарисовать ровные линии и окружности, а также измерить нужные размеры для создания цилиндра.

4. Резинка и точилка. Резинка поможет исправить ошибки, а точилка подержит ваши карандаши и ручки острыми для точной работы.

5. Вдохновение и терпение. Для рисования цилиндров вам понадобится фантазия и настойчивость. Изометрический рисунок может потребовать продолжительного времени и попыток, но результат стоит усилий.

Собрав все необходимые инструменты и материалы, вы будете готовы приступить к рисованию цилиндров в изометрии. Не забывайте практиковаться и экспериментировать с разными техниками, чтобы создать уникальные и интересные рисунки цилиндров.

Дистанционные курсы для педагогов

Выдаём документы установленного образца! Учителя о ЕГЭ: секреты успешной подготовки В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной Каждый второй ребенок в школе подвергался психической агрессии Академическая стипендия для вузов в 2023 году вырастет до 1 825 рублей Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи Минпросвещения России подготовит учителей для обучения детей из Донбасса В приграничных пунктах Брянской области на день приостановили занятия в школах

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи. Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов. Источник

Круг в перспективе.

Чтобы построить тело вращения в перспективе надо сначала разобраться с построением круга в перспективе, ведь тело вращения состоит из кругов. Круг в перспективе выглядит как эллипс, именно как эллипс, а не как овал. Эллипс и овал это совершенно разные геометрические фигуры и не надо их путать. В черчении, при построении изометрических изображений, эллипсы заменяют овалами потому, что овалы легче построить с помощью циркуля, эллипс с помощью циркуля не построишь. Во всяком случае, точное построение эллипса с помощью циркуля и линейки не возможно. 

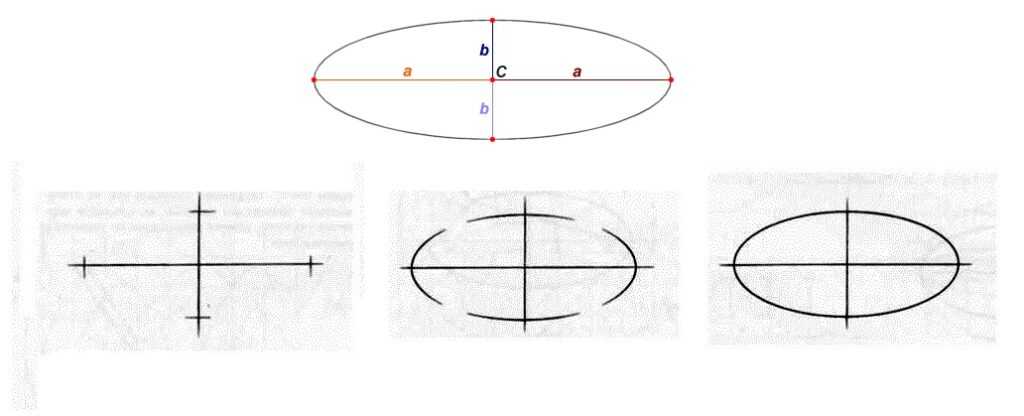
 Художники рисуют именно эллипсы, а не овалы. Художники строят эллипсы по двум осям. У эллипса есть большая ось и малая ось. Если предмет ровно стоит на горизонтальной плоскости и никуда не наклонен, то большая ось эллипсов будет строго горизонтальна, а малая ось вертикальна и совпадает с осью предмета (ось предмета ровно стоящего на горизонтальной плоскости всегда вертикальна). С построением предметов, имеющих форму тел вращения мы разберёмся чуть позже, для начала нам надо разобраться с построением эллипса (то есть круга в перспективе). Оси эллипса всегда перпендикулярны друг другу. Итак мы изображаем круг лежащий на горизонтальной плоскости. Изображаем мы его, естественно, в перспективе. То есть вместо круга мы видим эллипс. Мы определили ширину нашего эллипса (она совпадает с шириной круга) и определили видимую высоту. Проведя визирование и определив пропорции, мы выяснили, что высота нашего эллипса равна половине ширины.

Мы провели длинную горизонтальную линию (ось) и перпендикулярно ей провели вертикальную линию (ось) равную половине горизонтальной. Малая ось пересекает большую ось строго посередине и, соответственно, большая ось пересекает малую тоже строго посередине. Концы осей и есть те четыре точки по которым художники строят эллипс. Но построить правильный эллипс по четырем точкам художнику не очень опытному сложновато, неплохо бы ещё несколько дополнительных точек иметь в наличии. Как найти дополнительные точки при построении эллипса?

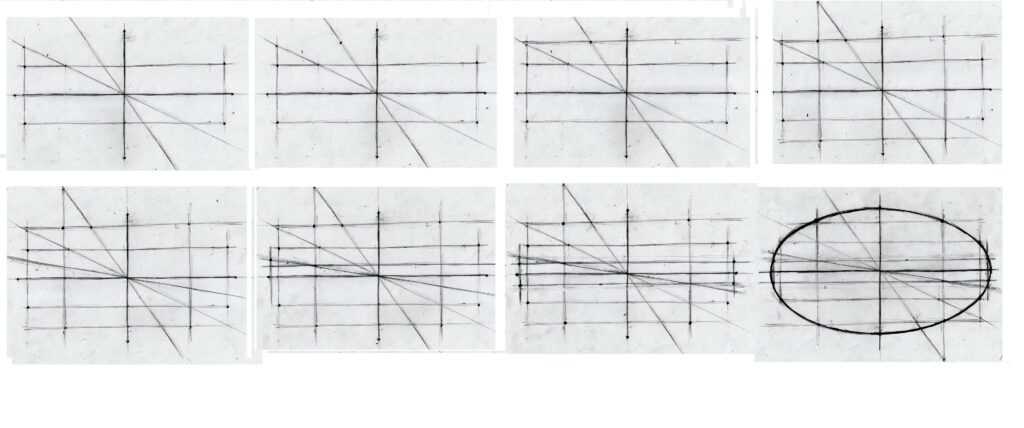
Такой способ есть. Через центр эллипса проводим наклонную прямую (как на рисунке), теперь откладываем на этой линии расстояние равное половине длины малой оси эллипса, ставим точку и через эту точку проводим линию параллельную большой оси эллипса. Теперь измеряем (карандашом) половину большой оси эллипса и откладываем это расстояние на той же самой линии. Через полученную точку проводим линию параллельную малой оси эллипса. На пересечении линий параллельных осям мы и находим дополнительную точку для построения эллипса. Теперь измеряем расстояние от дополнительной точки до длинной оси эллипса и откладываем его вниз, как бы отражая нашу дополнительную точку с другой стороны длинной оси. Проводим через эту (нижнюю) точку прямую линию параллельную длинной оси. Отражаем полученные точки по другую сторону малой оси. Теперь для построения эллипса у нас есть уже восемь точек, а не четыре. Мы можем провести еще одну линию через центр эллипса и найти еще четыре дополнительные точки для построения эллипса и у нас будет уже двенадцать точек для построения эллипса (способ нахождения этих точек такой же как и в первом случае). Эту операцию можно продолжать до бесконечность, однако двенадцать (максимум шестнадцать) точек вполне достаточно для того, чтобы эллипс у нас получился ровным и правильным. В конце концов Вы научитесь строить эллипс и по четырем точкам, как это делают опытные художники, к этому и надо стремиться.

Что такое тела вращения.

Давайте посмотрим на предметы изображенные на картинке. Что у них общего? Они круглые. То есть если мы посмотрим на них сверху, то увидим набор кругов. А если мы посмотрим на эти предметы сбоку то увидим, что левая и правая половинки такого предмета зеркально симметричны, то есть они как бы отражаются друг в друге как в зеркале. И с какой стороны мы бы не смотрели на такой предмет, он всегда будет выглядеть одинаково.

Конечно у таких предметов могут быть всякие ручки с одной или двух сторон, носики (например у чайников) и тому подобное, но это не в счёт, потому что ручки эти прикреплены к предмету, являются дополнением к основной форме предмета и на основную форму самого предмета они влияния не оказывают. 

В 3D редакторах (в том же максе) есть функция: нарисовать кривую и провращать её вокруг заданной оси, таким образом и создается тело вращения. Вот отсюда и научное название подобных тел.