Формулы расчёта цилиндра

Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник

Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса

Что такое объем

Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .

Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.

Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.

Объем и площадь других видов цилиндров рассмотрен в статьях:

Определение массы цилиндра

Наконец, стоит перейти непосредственно к теме статьи. Как определить массу цилиндра? Для этого необходимо знать его объем, формула для вычисления которого была представлена выше. И плотность вещества, из которого он состоит. Масса определяется по простой формуле: m = ρ*V, где ρ — плотность материала, образующего рассматриваемый объект.

Понятие плотности характеризует массу вещества, которое находится в единице объема пространства. Например. Известно, что железо имеет большую плотность, чем дерево. Это означает, что в случае одинаковых объемов вещества железа и дерева первое будет иметь намного большую массу, чем второе (приблизительно в 16 раз).

Объем цилиндрической полости

Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.

На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

Цилиндр может быть правильным или наклонным

Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.

Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.

Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник

Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.

Радиус основания цилиндра, является радиусом цилиндра.

Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.

Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

Шаг 1: Изучение формулы объема цилиндра

Перед тем, как перейти к вычислению объема цилиндра, необходимо понять, что такое цилиндр и какая формула используется для его объема.

Цилиндр — это геометрическое тело, состоящее из двух параллельных плоскостей, которые называются основаниями, и боковой поверхности, образованной прямым отрезком, соединяющим все точки оснований.

Формула для вычисления объема цилиндра выглядит следующим образом:

• Объем цилиндра (V) равен произведению площади основания (S) на высоту цилиндра (h).
• V = S * h

Теперь, когда мы знаем формулу, можно переходить к следующему шагу, вычислению объема цилиндра.

Цилиндр

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая  L.

Цилиндр называется прямым, если его образующие перпендикулярны основаниям.

Осевое сечение цилиндра  — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.

Основные понятия и свойства цилиндра:

1. Основания цилиндра равны и лежат в параллельных плоскостях.
2. Все образующие цилиндра параллельны и равны.
3. Радиусом цилиндра называется радиус его основания ($R$).
4. Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
5. Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
6. Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
7. Если высоту цилиндра увеличить в $m$ раз, то объем цилиндра увеличится в то же количество раз.
8. Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
9. Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.

Пример:

Сосуд в форме цилиндра заполнен водой до отметки $40$ см. Найдите, на какой высоте будет находиться уровень воды, если её перелить в другой сосуд в форме цилиндра, радиус основания которого в $2$ раза больше радиуса основания первого цилиндра. Ответ дайте в сантиметрах.

Решение:

Так как из сосудов перелили одинаковый объем жидкости, следовательно, при равных объемах отличаются радиусы и  высоты уровней жидкостей.

$V_1=V_2$;

$R_2=2R_1$, так как у второго цилиндра радиус в два раза больше радиуса первого.

$h_1=40;h_2-?$

Распишем объемы занимаемой жидкости в обоих сосудах и приравняем формулы друг к другу.

$V_1=πR_1^2·h_1=πR_1^2·40$;

$V_2=πR_2^2·h_2=π(2R_1)^2·h_2=4πR_1^2·h_2$.

$πR_1^2·40=4πR_1^2·h_2$

Получили уравнение, которое можно разделить на $πR_1^2$

$40=4 h_2$

Чтобы найти $h_2$ надо сорок разделить на четыре

$h_2=10$

Ответ: $10$

Площадь поверхности  и объем цилиндра

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

$S_{бок.пов.}=2πR·h$

Площадь поверхности цилиндра равна сумме  двух площадей оснований и площади боковой поверхности.

$S_{полн.пов.}=2πR^2+2πR·h=2πR(R+h)$

Объем цилиндра равен произведению площади основания на высоту.

$V= πR^2· h$

Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Составной цилиндр:

Чтобы найти объем составного цилиндра надо:

1. Разделить составной цилиндр на несколько цилиндров или частей цилиндра.
2. Найти объем каждого цилиндра.
3. Сложить объемы.

Площадь полого цилиндра

По толщине стенки и наружному диаметру

Формула полной поверхности цилиндра: 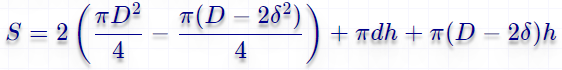Формула внутренней и внешней боковой поверхности цилиндра: Формула основания цилиндра: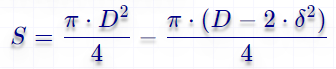

Посчитать

Через внутренний и наружный радиусы

Формула полной поверхности цилиндра: S = 2*pi*(r1-r2)+2*pi*(r1+r2)*hФормула внутренней и внешней боковой поверхности цилиндра: S = 2*pi*(r1+r2)*hФормула основания цилиндра: S = pi*(r1-r2)

Посчитать

По внутреннему диаметру и толщине стенки

Формула полной поверхности цилиндра: S = 2*pi*(d*δ+δ2)+2*pi*h*(d+δ)Формула внутренней и внешнейбоковой поверхности цилиндра: S = 2*pi*h*(d+δ)Формула основания цилиндра: S = pi*(d*δ+δ2)

Посчитать

Применение при расчете емкости сосудов

Цилиндрические сосуды, такие как канистры для хранения жидкостей или баки для топлива, построены на основе формулы объема цилиндра. Зная объем, который может вместиться в сосуд, мы можем рассчитать количество жидкости или топлива, которое в него заправим или храним. Это важная информация для планирования закупок или контроля запасов.

Например, если у вас есть цилиндрическая канистра, диаметр которой равен 30 сантиметрам, и вы знаете, что канистра заполняется на две трети емкости, вы можете использовать формулу объема цилиндра для расчета фактического объема:

V = π(15^2)h

Где h — высота жидкости в канистре. Если площадь дна канистры составляет 706,86 квадратных сантиметров (π(15^2)), то путем возведения значения площади в степень 2 вы получите объем, а умножение этого значения на две трети даст вам фактический объем, который вы сможете заполнить жидкостью.

Геометрическая интерпретация формулы объема цилиндра: основание, высота и радиус

Приветствую, друзья! Сегодня мы поговорим о геометрической интерпретации формулы объема цилиндра. Если вы когда-либо задавались вопросом, как расчитать объем цилиндра, то вы попали по адресу.

Для начала давайте вспомним, что такое цилиндр. Можно представить его как бокал или банку, то есть фигуру, имеющую два равных и параллельных основания, соединенных боковой поверхностью.

Теперь перейдем к главным игрокам нашего исследования — основание, высота и радиус цилиндра. Основание — это плоская фигура, ограничивающая его снизу и сверху. Как правило, основания цилиндра представляют собой две круглые плоскости.

Высотой цилиндра называется расстояние между его двумя основаниями. Она может быть любой, но все же для нашего исследования нам потребуется конкретная высота цилиндра. Представьте, что цилиндр — это ведро, наполненное водой. Высота цилиндра будет равна расстоянию от дна ведра до уровня воды. Вот так понятнее, не правда ли?

Но что насчет радиуса цилиндра? Радиус — это расстояние от центра основания до любой точки на его окружности. Представьте, что вы берете линейку и измеряете расстояние от центра круглой части цилиндра до его края. И это будет ваш радиус.

Итак, теперь мы знакомы с основанием, высотой и радиусом цилиндра. Но как эти параметры связаны с формулой объема цилиндра? Вот где начинается самое интересное.

Объем цилиндра можно рассчитать, используя формулу V = площадь основания * высота. Понимаете, что это означает? Если представить одно из оснований цилиндра как большой пирог, а высоту — как его толщину, то объем цилиндра можно рассматривать как количество пирога, которое вмещается внутрь цилиндра. Вкусно, правда?

Теперь, чтобы рассчитать объем цилиндра, вам необходимо знать площадь его основания и высоту. Площадь основания цилиндра равна площади круга и рассчитывается по формуле S = пи * радиус^2. Просто подставьте значение радиуса и вы получите площадь основания.

После того, как вы рассчитали площадь основания и знаете высоту, просто умножьте эти значения и получите объем цилиндра. Не забудьте умножить площадь основания на высоту, чтобы представить объем цилиндра в кубических единицах.

Вот такая простая и понятная геометрическая интерпретация формулы объема цилиндра! Теперь вы можете легко рассчитать объем любого цилиндра, зная его основание, высоту и радиус.

Друзья, надеюсь, эта статья была полезной для вас. Теперь вы можете разделить свои знания о геометрии с друзьями и семьей.

Увидимся в следующей статье! Пока!

Математический анализ возможных ошибок при вычислении объема цилиндра

Приветствую, уважаемые читатели! Сегодня мы поговорим о математическом анализе ошибок, которые могут возникнуть при вычислении объема цилиндра. Как только мы начнем рассматривать эту формулу, многие из вас могут сразу сказать «А кому это нужно? Я запомнил формулу в школе и никогда больше не задумывался!» Но подождите, друзья, ведь иногда даже простые формулы могут привести к ошибкам, и мы сегодня рассмотрим их, чтобы помочь вам избежать некорректных результатов.

Давайте вспомним формулу для вычисления объема цилиндра: V = πr^2h, где V — объем, π — число Пи (приближенно равно 3,14), r — радиус основания цилиндра и h — высота цилиндра. Кажется просто, верно?

Однако, реальная жизнь не всегда такая простая. Мы сталкиваемся с ошибками в математике ежедневно, и это неизбежно. Так что давайте посмотрим на некоторые распространенные ошибки и способы их предотвращения.

Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура.

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник, но две боковые стороны которого будут являться кривыми линиями.

Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг.

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс.

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса.

Математические Основы

Цилиндр, как и любая другая геометрическая фигура, имеет свои уникальные формулы для расчета объема

Важно понимать, как эти формулы выводятся и применяются для вычисления объема цилиндра

Формула Объема Цилиндра

Объем (V) цилиндра вычисляется по формуле:

\

где:

• r — радиус основания цилиндра,
• h — высота цилиндра,
• \(\pi\) — математическая константа, приблизительно равная 3.14159.

Принципы Расчета

• Радиус: Чтобы найти объем, необходимо знать радиус основания. Радиус — это расстояние от центра круглого основания до его края.
• Высота: Высота цилиндра измеряется как перпендикулярное расстояние между двумя основаниями.
• Использование \(\pi\): Константа \(\pi\) используется для вычисления площади круга, которая затем умножается на высоту для получения объема.

Примеры Расчета

1. Цилиндр с радиусом 3 м и высотой 5 м:

\

2. Цилиндр с радиусом 2 м и высотой 10 м:

\

Эти примеры иллюстрируют базовый принцип расчета объема цилиндра и демонстрируют, как изменение радиуса и высоты влияет на объем

Важно понимать эти математические принципы для корректного вычисления объемов в различных практических задачах

Однородный и полый цилиндры

Из полученного выше результата можно видеть, что медный цилиндр с относительно малыми размерами (10 см) обладает большой массой (28 кг). Это связано не только с тем, что он сделан из тяжелого материала, но и с тем, что он является однородным

Этот факт важно понимать, поскольку приведенную выше формулу для расчета массы можно использовать только в случае, если цилиндр полностью (снаружи и внутри) состоит из одного и того же материала, то есть является однородным

На практике же часто используют полые цилиндры (например, цилиндрические бочки для воды). То есть они сделаны из тонких листов какого-то материала, а внутри являются пустыми. Для полого цилиндра указанной формулой расчета массы пользоваться нельзя.

Формулы расчёта объёма цилиндра

Объем правильного цилиндра через радиус и высоту

Формула расчёта объема правильного цилиндра через радиус и высоту Вам необходимо указать радиус основания цилиндра (r) и высота цилиндра (h).
Онлайн калькулятор делает расчёт по формуле: V=pi*r2*h .

Посчитать

Объём полого цилиндра

Формула расчёта: V = pi*(r1-r2)*h

Посчитать

Формула расчёта: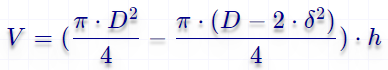

Посчитать

По внутреннему диаметру и толщине стенки

Формула расчёта: V = pi*(d*δ+δ2)*h

Посчитать

Через площадь основания и высоту

Формула расчёта объема правильного цилиндра через площадь основания и высоту Вам необходимо указать площадь основания цилиндра (S) и высота цилиндра (h).
Онлайн калькулятор делает расчёт по формуле: V=S*h.

Посчитать

Через диаметр основания и высоту

Формула расчёта объема правильного цилиндра через диаметр основания и высоту Вам необходимо указать диаметр основания цилиндра (d) и высота цилиндра (h).
Онлайн калькулятор делает расчёт по формуле: V=pi*d2/4*h.

Посчитать

Через диаметр основания и высоту

Формула расчёта: V = (α°/360)*pi*r2*h

Посчитать

Что такое объем

Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .

Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.

Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.

Объем и площадь других видов цилиндров рассмотрен в статьях:

🛢️ Когда требуется знать объем цилиндра?

Знание объема цилиндра может потребоваться в различных ситуациях, к примеру:

Расчет объема бака или резервуара: если вы планируете хранить жидкость или газ в баке или резервуаре, то может быть важно знать его объем, чтобы знать, сколько материала вы можете в него поместить.

Расчет объема емкости для транспортировки: если вы занимаетесь перевозкой жидкостей или газов, то может потребоваться знать объем емкости, чтобы убедиться, что вы можете перевезти нужное количество материала.

Расчет объема цилиндрических труб: если вы занимаетесь установкой трубопроводов или работой с другими цилиндрическими объектами, то может быть полезно знать их объем, чтобы правильно рассчитать количество материала, необходимого для работы.

Расчет объема бутылки или бочки: если вы хотите знать, сколько жидкости вы можете вместить в определенную бутылку или бочку, то калькулятор объема цилиндра может помочь рассчитать объем емкости.

Определение объема цилиндрических объектов, используемых в декоративных целях, например, колонн, скульптур и других элементов архитектуры и дизайна.

Также умение рассчитывать объем цилиндра пригодится в строительстве, химии и фармацевтике, механике и технике, производстве, учебе и творчестве.

🧮 Что такое калькулятор объема цилиндра?

Калькулятор объема цилиндра – это инструмент, который позволяет автоматически рассчитывать объем цилиндра по его размерам. Обычно калькулятор объема цилиндра предоставляет пользователю простую форму, где нужно ввести значение радиуса основания и высоты цилиндра, а затем нажать кнопку «Рассчитать». Калькулятор объема цилиндра может быть представлен в виде программы на компьютере или мобильном устройстве, а также в виде онлайн-сервиса на веб-сайте, как у нас.

Использование калькулятора объема цилиндра упрощает и ускоряет процесс расчета объема цилиндра, особенно если нужно рассчитать объем нескольких цилиндров или если значения радиуса и высоты цилиндра имеют сложные числовые значения. Калькулятор объема цилиндра может быть полезен в различных областях, включая науку, технику, строительство, производство, учебу и домашнее хозяйство.

Похожие калькуляторы

Вам могут пригодиться следующие калькуляторы на эту же тему:

• Калькулятор перевода миллиметров в дюймы. Введите длину в миллиметрах для перевода в дюймы.
• Калькулятор перевода дюймов в миллиметры. Введите длину в дюймах для перевода в миллиметры.
• Калькулятор перевода сантиметров в дюймы. Введите длину в сантиметрах для перевода в дюймы.
• Калькулятор перевода дюймов в сантиметры. Введите длину в дюймах для перевода в сантиметры.
• Калькулятор площади поверхности шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы) с помощью нашего онлайн-калькулятора.
• Калькулятор площади правильного шестиугольника. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью нашего онлайн-калькулятора.
• Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
• Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
• Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
• Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).

Объем жидкости в цилиндрической таре

Расчет объема жидкости в цилиндрической таре, лежащей на боку (создано по запросу пользователя).

Ага, сегодня я путем несложных умозаключений буду выяснять объем жидкости, находящейся в цилиндрической таре, лежащей на боку. И это не праздности ради, а дела для.

Цитирую запрос пользователя объем сегмента цилиндра (2): Доброго времени суток. Видел калькулятор объема сегмента цилиндра, но нужно немножко другое. По работе приходится измерять количество жидкости в таре. Так вот допустим тара цилиндрической формы R=1,13м и H=6,3м лежит на поверхности. Жидкости в таре 0,9м от поверхности. Вопрос: какой объем жидкости в таре?

Там дальше в запросе идут ссылки на решение, но это же не спортивно, поэтому я пошел своим путем ? Сразу замечу, что вторая, более сложная задача — объем жидкости в таре, лежащей под наклоном, еще ждет своего решения.

Вот калькулятор, который все считает, а ход рассуждений, как обычно, под ним.

Объем жидкости в цилиндрической таре

Итак, сформулируем задачу наглядно, и посмотрим на цилиндр в разрезе (см. рисунок). Если уровень жидкости m больше половины, то находим объем воздуха в оставшейся части, а потом вычитаем из общего объема — т. е. всегда сводим к случаю, изображенному на рисунке.

Формула объема всего цилиндра известна — площадь основания, помноженная на высоту.

А нам, значит, надо найти площадь фигуры, залитой синей жидкостью, и тоже помножить на высоту. Пытливый взгляд отметит, что фигура, залитая синей жидкостью, получается из сектора после вычета верхнего треугольника.

Площадь сектора находится как , где альфа — это угол дуги в радианах.

Угол дуги нам неизвестен. Разберемся сначала с ним. Линия, опущенная вертикально вниз делит верхний треугольник на два прямоугольных треугольника. Гипотенуза у них равна R, а катет, прилежащий к верхнему углу, равен R-m. Таким образом,

и ответ нам Javascript даст как раз в радианах, то что нам нужно.

Теперь разберемся с верхним треугольником. Он равнобедренный, бедра равны R, а основание нам неизвестно. Найдем его. А оно как раз равно удвоенному противолежащему катету, который, согласно всем известной теореме Пифагора равен

Зная все стороны треугольника, нетрудно найти его площадь по формуле Герона — Расчет площади треугольника по формуле Герона.

Вот, собственно, и все. Мы знаем площадь сектора и площадь треугольника. Вычитаем площадь треугольника из площади сектора, домножаем на высоту цилиндра (или длину цилиндра, с учетом того, что он лежит) и получаем результат.

Подстановка значений в формулу

Теперь, когда у нас есть формула для вычисления объема цилиндра, давайте подставим в нее конкретные значения и получим окончательный результат.

Объем цилиндра вычисляется по следующей формуле:

V = π * r^2 * h

Где:

• V — объем цилиндра
• π — число Пи (приближенное значение 3.14159)
• r — радиус основания цилиндра
• h — высота цилиндра

Например, предположим, что радиус основания цилиндра равен 5 см, а высота цилиндра составляет 10 см. Тогда, подставив эти значения в формулу, мы получим:

V = 3.14159 * 5^2 * 10 = 3.14159 * 25 * 10 = 785.39875 см³

Таким образом, объем цилиндра равен 785.39875 см³ при данных значениях радиуса и высоты.

Онлайн калькулятор

Найти чему равен объем цилиндра (V) можно зная (либо-либо):

• радиус r и высоту h цилиндра
• диаметр d и высоту h цилиндра
• площадь основания S_o и высоту h цилиндра
• площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра V если известны его радиус r и высота h?

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3

Зная диаметр d и высоту h

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ ( 1 /₂) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3

Зная площадь основания S_o и высоту h

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см 2 , то:

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см 2 , то:

V = 30 2 / _{4 ⋅ 3.14⋅ 5} = 900 /_62.8 = 14.33 см 3

Формулы

Объем цилиндра

Объем цилиндра можно найти, умножив площадь его основания на высоту. Основанием кругового цилиндра является круг радиусом r. Площадь поверхности круга можно найти как πr², поэтому объем цилиндра, V, можно найти по следующей формуле:

V = πr²h

Площадь боковой поверхности

Площадь боковой поверхности цилиндра — это площадь, занимаемая его изогнутой стороной. «Развернув» боковую поверхность цилиндра на плоскость, мы получим прямоугольник, одна из сторон которого равна h, а другая — окружности базового круга. Площадь прямоугольника можно найти, перемножив длины его сторон. Окружность базового круга можно найти как 2πr, поэтому площадь боковой поверхности цилиндра можно найти по следующей формуле:

L = 2πrh

Площадь базовой поверхности (и площадь верхней поверхности)

Площадь верхней поверхности, T, и площадь поверхности основания, B, кругового цилиндра эквивалентны, поскольку верхняя и нижняя поверхности представлены одинаковыми окружностями. B = T можно найти с помощью формулы площади поверхности круга:

B = T = πr².

Геометрический вывод

Давайте представим себе цилиндр – это геометрическое тело, состоящее из двух оснований и боковой поверхности, которая образует круглый рубашку. Чтобы найти объем цилиндра, мы должны учесть его геометрические свойства.

Объем цилиндра можно представить как сумму объема двух элементов: объема основания и объема боковой поверхности.

Объем основания цилиндра – это площадь круга, умноженная на высоту цилиндра.

Объем боковой поверхности цилиндра – это площадь круга, умноженная на его окружность.

Суммируя объем основания и объем боковой поверхности, мы получим формулу для объема цилиндра:

Объем цилиндра = Площадь основания * Высота + Площадь основания * Окружность