Презентация проекта «геометрия пожарной каланчи». — презентация

Цилиндр в архитектуре

Презентация полезна тем, что показывает повсеместное архитектурное использование фигуры цилиндр.

Содержимое разработки

Государственное бюджетное профессиональное образовательное учреждение

«Ковровский медицинский колледж имени Е. И. Смирнова»

Специальность: «Акушерское дело»

Подготовил студент 05 – А группы

В современном мире в архитектуре начинается использование всё более новых, сложных и интересных фигур. Людям становится скучно жить среди однообразных пятиэтажных домов

Моё внимание привлёк цилиндр. Фигура не простая сама по себе, а применить её в строительстве – сложно и неоднозначно

В моей презентации я хочу рассказать Вам о том, что же такое цилиндр, поведаю о некоторых его особенностях и покажу на примере его использование в одной из главных наук мира – архитектуре.

Цилиндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её под прямым углом.

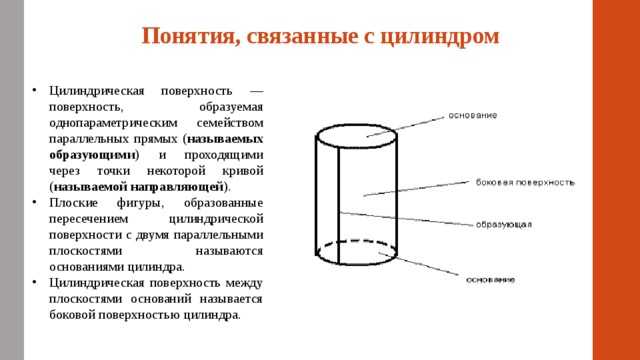
Понятия, связанные с цилиндром

• Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых ( называемых образующими ) и проходящими через точки некоторой кривой ( называемой направляющей ).
• Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями называются основаниями цилиндра.
• Цилиндрическая поверхность между плоскостями оснований называется боковой поверхностью цилиндра.

Хронология цилиндра в архитектуре

Цилиндры в древней архитектуре

Сами цилиндры появились в архитектуре ещё в древние века, они выступали в роли несущих и второстепенных элементов. Конечно, всё началось с округлых колонн. Их применяли всё время и такой архитектурных ход был распространён. Здания же цилиндрической формы появились лишь в наше время.

Первые каменные колонны применили в Древнем Египте при постройке Пирамиды Джосера в 2650 году до н.э. Впервые в истории была применена каменная постройка из 40 колонн высотой каждой из них в 10 метров. Так как эти колонны были первыми на земле, архитектор Имхотеп соединил каждую из них со стеной с одной стороны.

Также одни из самых популярных сооружений цилиндрической формы является Колизей в Риме.

Цилиндры в современной архитектуре

Среди компонентов современной архитектуры можно найти немало кубических конструкций (особенно из стекла), треугольников в виде, например, фронтонов; и случайные изгибы тоже часто встречаются. Но что насчёт цилиндров? При их упоминании в связи со строительством зданий вспоминается стиль арт-деко, который весьма недолго был популярен в начале 20 века.

Цилиндры и закруглённые углы использовались им для передачи динамики плавных движений. В поле ретроспективы также оказываются башенки средневековых сооружений и примитивные промышленные здания Америки.

Тем не менее, цилиндры нашли себе место в современной архитектуре. Редкие образцы производят сильнейшее впечатление, если перекликаются с контекстом.

Есть два вопроса, отсутствие ответов на которые, объясняет нежелание архитекторов включать цилиндрические формы в структуру зданий, тем более жилых. Что будет находиться внутри? И как связать цилиндр с остальной частью здания эмоционально и физически?

По первому пункту можно заметить, что внутри цилиндров обычно возводятся лестницы, которые наполняют всю конструкцию практическим смыслом. Что касается второго вопроса, здесь будут продемонстрированы здания, смежные стены которых разделены цилиндрическим элементом, который может выдаваться вперёд или стоять вровень с фасадом.

Ещё с древних времен люди использовали в строительстве цилиндрические формы зданий. Мы убедились, что непросто выбрать такой сложной фигуре своё место в архитектурном пространстве. Но, хоть это и сложно, выглядит потрясающе!

Как понять геометрию 7 класса?

         Наступил сентябрь. Моя дочь, радостная и отдохнувшая за тёплые летние месяцы, пошла в 7 класс. Через несколько дней она пришла ко мне и сказала:      – Ты знаешь, пап, мы сегодня начали новый предмет «Геометрия». Учительница сказала, что мы будем изучать его целых 5 лет, до самого выпускного!         Она уже задала домашнее задание. Ты сможешь мне помочь?         – Безусловно, я помогу тебе. Но для этого мы с тобой отправимся в Древний Египет, побываем в Древней Греции, в Средневековой Европе, во Франции времён императора Наполеона и ещё во многих других местах, где ты узнаешь о геометрии много нового и интересного. А потом мы начнём с тобой заниматься теорией и практикой, и, я думаю, за 12 уроков мы с тобой осилим весь годовой курс геометрии.  И после этого тебе будет легко понять геометрию 7 класса. Ты согласна?         – Конечно,  согласна. А когда мы туда отправимся?        – Ну, если у тебя есть полчаса, то мы отправимся прямо сейчас, –  ответил я дочери.

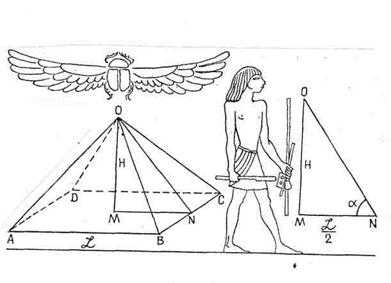         — Итак, Древний Египет. Широкий Нил, который величаво несёт свои воды через всю страну. Вокруг реки собираются люди и звери, ведь вода – это сама жизнь. Цветущие оазисы, поля ячменя и пшеницы,  плантации финиковых пальм, каналы, прорытые в разные стороны – всё это было в Древнем Египте.          Нил жил по своим законам. Каждый год в начале июля начинался его разлив, который достигал максимума к октябрю, после чего начинался спад воды, и к декабрю всё возвращалось к исходному положению. Площади, которые затапливались Нилом, были как никакие другие пригодны для земледелия. Но, чтобы работать на них, древним египтянам надо было успевать засеять, вырастить и собрать урожай до наступления следующего разлива. А для этого требовался точный расчёт.         Необходимо было научиться рассчитывать площади затапливаемых земель, объём водохранилищ для сбора дополнительной воды, размеры каналов для отвода этой воды и многое-многое другое. Я уже не говорю о древних архитекторах и зодчих, которые рассчитали и построили величайшие сооружения в мире – пирамиды. В общем, без знания и понимания геометрии, её законов, принципов и постулатов вряд ли древним египтянам удалось сделать то, над чем восторгается многие сотни и тысячи лет весь остальной мир.          – Значит, та геометрия, которую мы сегодня начали изучать, родилась в Древнем Египте? – спросила меня Ира.          – Нет, немного не так. Та геометрия, о которой ты говоришь, родилась в Древней Греции.  Рассказывая о Египте, Ниле, его разливах, я лишь хотел показать тебе, какой древней наукой является геометрия. Кстати, если уж говорить о древности, то математика  была создана в первую очередь, как приложение к геометрии и лишь потом преобразовалась в отдельную науку.           А теперь – к истокам – в Древнюю Грецию. Послушаем беседы Платона со своими учениками;  побываем в Сиракузах в гостях у великого Архимеда; услышим  теорему от самого Пифагора; присоединимся  к Фалесу из Милета во время доказательства им ПЕРВОЙ ТЕОРЕМЫ по геометрии; ну, и наконец, увидим отца геометрии – Евклида, выводящего свои постулаты и аксиомы, которыми мы пользуемся и по сей день.          – Вперёд, к истокам! – сказала Ира.
Продолжение следует…

Метки: Воспитание детей, Геометрия, МотивацияРубрика: Геометрия, Советы родителям, Читатель 21 века |

Где встречаются геометрические фигуры в нашей жизни?

Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах. 

Люди давно заинтересовались разнообразием геометрических фигур. Ещё для первобытных людей важную роль играла форма окружавших их предметов. Овладевая миром, люди знакомились с простейшими геометрическими формами. Сначала они изготавливали орудия труда относительно правильной формы, потом научились их совершенствовать. Специальных названий для геометрических фигур тогда, конечно, не было. Их придумали значительно позже. Когда люди стали строить дома, им пришлось ещё глубже разбираться в особенностях разных фигур, чтобы понять, какую форму следует придавать стенам и крыше, какой формы должны быть брёвна или каменные глыбы. Сам того не зная, человек всё время занимался изучением фигур: женщины, изготавливая одежду, охотники — наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.

И в современном мире без этих знаний не прожить.

Где же встречаются геометрические фигуры в нашей жизни?

Возможно, кто-то считает, что различные линии фигуры «водятся» только в книгах учёных математиков. Однако, если посмотреть вокруг, становится понятно, что многие предметы имеют форму, похожую на основные геометрические фигуры. Просто мы не всегда это замечаем. Немало замечательных геометрических фигур встречается в окружающей нас природе. Поле имеет форму прямоугольника, река — кривой линии, озеро — круга, кристалл соли — форму куба, обычная горошинка, капелька росы — форму шара. Красивы и разнообразны многогранники — кристаллы горного хрусталя. Но и в привычной жизни основные геометрические фигуры тоже повсюду. Это здания, строения, транспорт, интерьер квартиры, даже посуда и предметы одежды. К примеру, женская юбка — это трапеция, тарелка — круг, дом — квадрат и треугольник, а в трубе — цилиндр. 

Знать все фигуры, их виды, названия и свойства очень важно. Систематизирует знания о геометрических фигурах и изучает их свойства математическая наука — геометрия

Наука эта очень важная, её применение просто бесценно во все времена и независимо от профессии. Без знаний геометрии не обходится ни рабочий, ни инженер, ни архитектор, ни художник. И очень важно начать осваивать эту науку в раннем возрасте. 

Прекрасным помощником ребёнку в этом станет образовательная платформа iSmart. Основные виды геометрических фигур, их свойства, задачи на нахождение площади фигур и многое другое есть на платформе в разделе «Математика». Тут собраны несколько тысяч заданий на освоение этих тем, не повторяющиеся при многократной отработке. Занимаясь на , школьники начальных классов досконально разберутся в основах геометрии. Это даст им хорошую базу по предмету для учёбы в средних и старших классах. Кроме того, интерактивные задания красочные, интересные, увлекательные.

Итак,

Как определить цилиндр в геометрии?

Для определения цилиндра необходимо знать несколько характеристик:

1.	Радиус основания (R).
2.	Высоту цилиндра (h).

Радиус основания (R) — это расстояние от центра основания до любой точки его окружности. Он одинаков для обоих оснований цилиндра.

Высота цилиндра (h) — это расстояние между плоскостями оснований.

Для вычисления объема цилиндра используется формула:

V = π * R^2 * h

где V — объем цилиндра, R — радиус основания, h — высота цилиндра.

А для вычисления площади поверхности цилиндра используется формула:

S = 2π * R * (R + h)

где S — площадь поверхности цилиндра, R — радиус основания, h — высота цилиндра.

Теперь, зная формулы для вычисления объема и площади поверхности цилиндра, вы сможете более точно определить эту геометрическую фигуру и решать задачи, связанные с цилиндром.

Цилиндр простыми словами для чайников

Цилиндр — это геометрическое тело, которое выглядит как стакан или банка. Оно имеет две круглые основы и боковую поверхность, которая выглядит как обернутый вокруг него прямоугольник. Основы цилиндра находятся на одном уровне и параллельны друг другу.

Представьте, что вы берете кусок теста и скатываете его в форме цилиндра. Края теста образуют две круглые основы, а остальная часть теста образует боковую поверхность цилиндра.

Важно отметить, что все вертикальные линии, проведенные от одной основы к другой, будут иметь одинаковую длину. Это расстояние называется высотой цилиндра

Также важно отметить, что диаметр основы — это расстояние между двумя точками на круглой основе через ее центр.

Цилиндры встречаются в повседневной жизни очень часто. Например, банки консервов, стаканы, колонки и даже часть столба — все они имеют форму цилиндра.

Цилиндры могут иметь разные размеры. Некоторые из них могут быть высокими и узкими, как стакан, а другие — низкими и широкими, как банка. Но независимо от их размера, все цилиндры имеют одинаковую форму и особенности.

Теперь, когда вы знаете основные понятия о цилиндре, вы можете легко определить его форму и рассчитать различные характеристики, такие как площадь поверхности и объем. Знание о цилиндре может быть полезным при решении задач в геометрии, а также при работе с реальными объектами, которые имеют форму цилиндра.

Подписи к слайдам:

Научно — исследовательская работа на тему: «Геометрические формы и фигуры в архитектуре города Мелеуз » Выполнили:обучающиеся 6 а класса МОБУ СОШ № 5г. Мелеуз Мишкевич Альбина иМазлова Екатерина

Цель нашей работы: выяснить, как геометрия украшает город Мелеуз; исследовать какие геометрические формы, тела и фигуры встречаются на улицах нашего города.Задачи:1.Изучить разнообразие геометрических форм и фигур.2.Рассмотреть варианты использования геометрических фигур и тел в отдельных архитектурных объектах нашего города.3.Выяснить какие геометрические фигуры встречаются чаще и почему.

Объекты исследования: архитектурные здания и строения, улицы г. Мелеуз.Предмет исследования: геометрические формы и фигуры в архитектуре города Мелеуз.Гипотеза исследования: геометрические фигуры, являясь идеальными объектами, находят свое наглядное воплощение в разнообразных архитектурных сооружениях.

Методы исследования:1.Проанализировать литературу по исследуемой теме.2.Рассмотреть многообразие архитектурных сооружений города Мелеуз.3. Показать какую форму или совокупность геометрических фигур имеют выбранные сооружения.4. Анкетирование.5. Эксперимент.6. Оформление результатов исследования. Актуальность работы Архитектурные объекты являются неотъемлемой частью нашей жизни. Наше настроение, мироощущение зависят от того, какие здания нас окружают. Назрела необходимость исследования того многообразия объектов, которые появились в нашем мире. 1) Многоугольники, виды многоугольников ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ФОРМЫ 2) Округлые формы ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ФОРМЫ 3)Многранники ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ФОРМЫ 4)Тела вращения ВСЁ ЛИ ВАС УСТРАИВАЕТ В АРХИТЕКТУРЕ НАШЕГО ГОРОДА? КАКИЕ АРХИТЕКТУРНЫЕ СООРУЖЕНИЯ ВЫ ХОТЕЛИ БЫ ВИДЕТЬ В НАШЕМ ГОРОДЕ? КАКИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ФОРМЫ ИСПОЛЬЗУЮТСЯ В АРХИТЕКТУРЕ НАШЕГО ГОРОДА? КАКИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ФОРМЫ ДЕЛАЮТ ЗДАНИЯ БОЛЕЕ ЧЕТКИМИ И ВЫРАЗИТЕЛЬНЫМИ? ЭКСПЕРИМЕНТАППЛИКАЦИЯ « ЕСЛИ БЫ Я БЫЛ АРХИТЕКТОРОМ» Работу выполнили – 30 учеников (1 б класс)28 учеников — использовали многоугольники (прямоугольник, квадрат, ромб) 2 ученика – использовали круг и овал. ПЕРВОЕ НАПРАВЛЕНИЕ ВТОРОЕ НАПРАВЛЕНИЕ СЛАЙД-ШОУ « ГЕОМЕТРИЯ НАШЕГО ГОРОДА» ВЫВОД: Все архитектурные сооружения города Мелеуз состоят из геометрических фигур и их совокупностей (в основном многогранников). ЛЕ КОРБЮЗЬЕ: «……Окружающий нас мир — это мир геометрии, чистой, истинной, безупречной в наших глазах. Все вокруг — геометрия. Никогда мы не видели так ясно таких форм, как круг, прямоугольник, угол, цилиндр, шар, выполненных так отчетливо, с такой тщательностью и так уверенно».

Ровно 220 лет назад, 15 января 1797 года, шляпный мастер Джеймс Хетерингтон впервые вышел из своего дома Лондоне с цилиндром на голове.

Появление мужчины шокировало окружающих: барышни теряли сознание, дети кричали, собаки разрывались от лая. Тот день для первого цилиндроносца закончился не слишком удачно: одного из обескураженных очевидцев его шляпного дебюта сбили с ног и он сломал руку. Виновника доставили в полицию и присудили уплатить штраф 500 фунтов стерлингов.

Несмотря на провальный дебют, цилиндр последующие 100 лет оставался наиболее популярным предметом шляпного гардероба у мужчин.

Известный шляпный модельер Ирина Белопухова рассказала Лайфу об истории создания цилиндра и его значении.

— Цилиндр — один из самых интересных и важных головных уборов в истории. Он давал мужчине то, что ему всегда нужно, — высокий рост. Соответственно, и значительность в образе. Вот, например, Пушкин очень любил и всегда ходил в высоком цилиндре (рост Пушкина составлял примерно 165 см. — Прим. Лайфа). Эта шляпа вытягивает фигуру и придаёт ей стать, вот в чём её секрет, — рассказала Белопухова.

Оригинальная и функциональная мебель

Цилиндры предоставляют множество возможностей для создания оригинальной и функциональной мебели. Их простая форма и разнообразие материалов, из которых они могут быть сделаны, позволяют реализовать самые необычные идеи.

Одной из популярных идей является использование цилиндров в качестве столиков. Маленький цилиндр может служить небольшим журнальным столиком рядом с диваном или креслом. Более крупные цилиндры можно использовать как столы для обеденной зоны или рабочего пространства. Их высоту можно регулировать, что делает их удобными и функциональными.

Использование цилиндров в качестве столиков помогает создать уникальный интерьер в вашем доме или офисе. Вы можете подобрать цилиндры в разных цветах и размерах, чтобы сочетание из них стало настоящей художественной инсталляцией. Такая мебель станет ярким акцентом в вашем интерьере и привнесет оригинальность и креативность в обстановку.

Кроме столиков, цилиндры можно использовать в качестве подставок для растений. Они будут выглядеть стильно и привлекательно, особенно если они сделаны из натуральных материалов, таких как дерево или керамика. Благодаря своей форме, цилиндр позволит подчеркнуть красоту растений и создать гармоничную композицию.

Еще одним интересным способом использования цилиндров в мебели является создание модульных систем. Вы можете соединять цилиндры между собой, чтобы создать стеллажи, шкафы или даже кровати. Это позволит вам подстраивать конфигурацию мебели под ваши нужды и менять ее при необходимости.

Также можно использовать цилиндры в качестве обивки для мягкой мебели. Их форма поможет создать необычный и стильный дизайн. Например, подушки в форме цилиндров будут выглядеть элегантно и необычно на диване или кресле. Вы также можете обшить цилиндры тканью и использовать их в качестве подушек для сидений или спинок стульев.

Коротко говоря, цилиндры могут быть использованы для создания оригинальной и функциональной мебели. Их простая форма и разнообразие материалов делают их универсальными и позволяют воплотить в жизнь самые нестандартные идеи.

Функциональное использование медного цилиндра в химической промышленности

Медные цилиндры играют важную роль в химической промышленности благодаря своим уникальным свойствам и широкому спектру функциональности. Они используются в различных процессах производства, где требуется высокая прочность, химическая стойкость и теплопроводность.

Одним из основных применений медных цилиндров является их использование в качестве реакторов. Медь хорошо сопротивляется коррозии и окислению, что делает ее идеальным материалом для контакта с агрессивными химическими веществами. Цилиндры из меди обычно используются для проведения различных химических реакций, включая окисление, гидрирование и нитрирование. Благодаря высокой теплопроводности меди, реакции в медных цилиндрах могут происходить более эффективно и равномерно, что способствует улучшению качества и выхода продукции.

Еще одним функциональным использованием медных цилиндров является их применение в процессе дистилляции и фракционирования. Медь обладает высокой теплопроводностью и способностью эффективно передавать и распределять тепло. Благодаря этому, медные цилиндры могут использоваться в качестве конденсаторов или сепараторов для отделения и сортировки различных химических соединений по их кипящим точкам. Такой процесс может быть необходимым для получения высокочистых продуктов и разделения смесей на их компоненты.

Кроме того, медные цилиндры находят применение в процессах электролиза и электрохимии. Медь является хорошим проводником электричества, поэтому цилиндры из меди могут использоваться для создания электродов или контактов в электролитических ячейках. Они играют важную роль в процессах гальванизации, электролиза металлов и электрохимического осаждения различных веществ.

• Медные цилиндры также широко используются в качестве теплообменных элементов в различных системах охлаждения и обогрева.
• Они могут быть использованы в качестве соляний и контейнеров для хранения химических веществ.
• Медные цилиндры могут быть применены в процессе изготовления и обработки различных материалов, например, при ламинировании металла.
• Они также могут использоваться в процессе очистки воды и других жидкостей от загрязнений применением химических реагентов.

Геометрические особенности цилиндра

Цилиндр — это трехмерное геометрическое тело, образованное плоскостью (дна цилиндра) и кривой (боковой поверхностью цилиндра), состоящей из прямых сегментов (объемный элемент цилиндра).

Основные характеристики цилиндра:

• Высота цилиндра: расстояние между дном и вершиной цилиндра.
• Радиус цилиндра: расстояние от центра дна цилиндра до любой точки на его боковой поверхности.
• Диаметр цилиндра: удвоенное значение радиуса цилиндра. Диаметр — это расстояние между двумя точками на боковой поверхности цилиндра через его центральную ось.

Цилиндры могут быть разных типов в зависимости от формы и положения дна и боковой поверхности:

1. Прямой цилиндр: дно и боковая поверхность параллельны друг другу.
2. Образный цилиндр: дно и боковая поверхность не параллельны, но взаимно перпендикулярны.
3. Усеченный цилиндр: верхнее и нижнее основания цилиндра не параллельны, а боковая поверхность представляет собой усеченный конус.
4. Наклонный цилиндр: дно и боковая поверхность наклонены друг к другу.

Цилиндры могут использоваться в различных областях, таких как строительство, инженерия, архитектура, механика и т. д. Некоторые примеры применения цилиндров:

Примеры использования цилиндров	Описание
Колонны и столбы	Цилиндрическая форма используется для создания поддерживающих структур, таких как колонны и столбы, которые могут выдерживать внешнее давление и нагрузку.
Баллоны и цистерны	Цилиндрическая форма используется для создания баллонов, цистерн и емкостей, которые могут содержать газы, жидкости и другие материалы.
Рубашки цилиндра двигателя	Цилиндрическая форма используется для создания рубашек цилиндров двигателя, в которых происходит сгорание топлива и движение поршней.
Трубы	Цилиндрическая форма используется для создания труб, которые широко применяются в строительстве, водоснабжении, отоплении и других отраслях.

Рубрики

• Воспитание детей (55)
  • Воспитание детей раннего возраста (11)
  • Ошибки воспитания (6)
  • Ошибки родителей (4)
  • Папа+Мама+Я=Семья (7)
  • Правила для родителей (4)
  • Про любовь (4)
  • Читатель 21 века (8)
• Геометрия

  Геометрия 7 класс (2)

  (3)

• Загадки (5)
• Математика ГИА (15)
  • Задание № 1 (7)
  • Задание № 3 (4)
  • Задание № 4 (4)
• Математические стихи (2)
• Праздники (15)
  • 23 февраля (1)
  • 8 Марта (2)
  • День Победы – 9 Мая (2)
  • День числа Пи (1)
  • Масленица (8)
• Притчи о жизни (34)
  • Аудио-притчи (28)
  • Притчи о любви (4)
• Сказки (50)
  • Аудио-сказки Сергея Панчешного (6)
  • Башкирские сказки (3)
  • Белорусские сказки (2)
  • Латышские сказки (3)
  • Литовские сказки (1)
  • Русские сказки (6)
  • Сказки о животных и птицах (5)
  • Сказки о природе (6)
  • Сказки о растениях (2)
  • Сказки Сергея Панчешного (14)
  • Украинские сказки (8)
  • Эстонские сказки (5)
  • Японские сказки (1)
• Советы родителям (4)
• Успех (21)
• Хокку на каждый день (169)

Основные геометрические фигуры

Соединённые между собой точки образуют линии, а соединённые между собой линии — основные геометрические фигуры на плоскости. 

Геометрические фигуры бывают плоские или двухмерные (2D) и объёмные пространственные, или трёхмерные (3D). Они ограничены замкнутой поверхностью своей наружной границы.

А если у геометрической фигуры все точки не находятся в одной плоскости, то она объёмная. К ним относятся шар, конус, цилиндр, сфера, пирамида и др.

Разберём плоские фигуры.

Треугольник

Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.

 Есть три вида треугольников:

• Прямоугольный — когда один угол прямой, другие два меньше 90 градусов.
• Остроугольный — когда градус его углов больше 0, но меньше 90 градусов.
• Тупоугольный — когда один угол тупой, то есть больше 90 градусов, а два других — острые.

Треугольники имеют следующие свойства:

• в треугольнике напротив большего угла лежит большая сторона и наоборот;
• сумма углов треугольника всегда равна 180 градусам;
• все углы равностороннего треугольника равны 60 градусам;
• в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (но это изучается уже в старших классах).

Вершины треугольников обозначаются заглавными буквами латинского алфавита: A, B, C и др.

Примеры треугольников:

Окружность

Окружность — геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом от центра расстоянии. 

Круг

Часть плоскости, находящаяся внутри окружности, называется кругом. То есть, окружность — это граница круга. А расстояние от центра окружности до любой точки на ней называется радиусом. Диаметр круга — это отрезок, который соединяет две точки на окружности и проходит через её центр. Диаметр круга равен двум его радиусам.

Прямоугольник

‍Прямоугольник — это фигура, состоящая из четырёх сторон и четырёх прямых углов, у которой:

• противоположные стороны равны между собой;
• диагонали равны и делятся в точке пересечения пополам;
• около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагоналей.

Квадрат

Квадрат — это тот же прямоугольник, у которого:

• все стороны равны;
• все углы равны и составляют 90 градусов;
• диагонали равны и перпендикулярны;
• центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.

Трапеция

Четырёхугольник, у которого две стороны параллельны, а две — нет, называется трапецией. Если сумма длин оснований трапеции равна сумме длин боковых сторон, в неё можно вписать окружность. 

Параллелограмм и ромб

Параллелограмм — четырёхугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм с равными сторонами.

Параллелограмм имеет следующие свойства:

• противоположные стороны и углы равны;
• сумма двух любых соседних углов равна 180 градусам;
• диагонали пересекаются и точкой пересечения делятся пополам;
• каждая диагональ делит фигуру на два равных треугольника.

Цилиндр своими словами для детей

Цилиндр — это фигура, похожая на банку из-под кока-колы или на карандаш. Он состоит из двух круглых крышек (как у банки) и боковой поверхности, которая выглядит как обернутая вокруг него бумажка.

Чтобы представить себе цилиндр, можно взять два круглых картона, один большой и один маленький. Большой круг станет основанием цилиндра, а маленький — его крышкой. Затем нужно взять лист бумаги и свернуть его вокруг картона, чтобы он стал боковой поверхностью.

Цилиндры бывают разных размеров. Например, банка из-под кока-колы — это маленький цилиндр, а газовые баллоны — большие цилиндры. Также цилиндры могут быть высокими и низкими. Например, карандаш — это высокий цилиндр, а тарелка — низкий цилиндр.

Цилиндры используются в разных сферах жизни. Например, в медицине они используются для хранения лекарств, а в строительстве — для создания труб и столбов. Также цилиндры можно найти в автомобилях, воздушных шарах и многих других местах.

Цилиндр имеет некоторые особенности. Например, его две крышки всегда круглые и параллельны друг другу. Также расстояние между крышками называется высотой цилиндра. А площадь боковой поверхности цилиндра можно найти, умножив окружность одной из крышек на высоту.

В общем, цилиндр — это простая и интересная фигура, которая встречается в нашей жизни повсюду. Она имеет свои особенности, но легко понять и представить себе.

Используемая литература:1. Белова, Т.И. Вычисление неопределенных интегралов. Обыкновенные дифференциальные уравнения. Компьютерный курс: учеб. пособие / Т.И.Белова, А.А.Грешилов, И.В.Дубограй; Ред. А.А.Грешилов. — М.: Логос, 2004. — 184 с. + 1 эл. опт. диск (CD-ROM).2. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. — 22-е изд., перераб. — СПб.: Профессия, 2006. — 432 с.3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. — 22-е изд., перераб. — СПб.: Профессия, 2005. — 432 с.4. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. — 4-е изд., стереотип. — М.: Дрофа, 2004. — 725 с.5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч. 1. Дифференциальное и интегральное исчисление / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; Ред. В.А.Садовничий. — 3-е изд., испр. — М.: ДРОФА, 2001. — 725 с.6. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч.2. Ряды, несобственные интегралы, ряды Фурье, преобразование Фурье / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; ред. В.А.Садовничий . — 3-е изд., испр. — М.: ДРОФА, 2001. — 712 с.7. Голоскоков, Д.П. Уравнения математической физики. Решение задач в системе Maple: учеб. для вузов / Д.П.Голоскоков. — СПб.: Питер, 2004. — 538с.8. Гурова, З.И. Математический анализ. Начальный курс с примерами и задачами: учеб. для втузов / З.И.Гурова, С.Н.Каролинская, А.П.Осипова; Ред. А.И.Кибзун. — М.: Физматлит, 2002. — 351 с.9. Лукьянов, А.В. Обыкновенные дифференциальные уравнения: учеб. пособие по решению задач / А.В.Лукьянов, Ю.Д.Погуляев. — Челябинск: Полиграф-Мастер, 2006.10. Математический анализ в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов . — 5-е изд., испр. — М.: ФИЗМАТЛИТ, 2002. — 479 с.Значение термина Цилиндр на academic.ru

Геометрия 11 класс

«Задачи по стереометрии» — Длина окружности. Объм шара и его частей. Диаметр свинцового шара. Найдите объем пирамиды. Найдите площадь поверхности многогранника. Найдите угол многогранника. Найдите квадрат расстояния между вершинами. Найдите объем V части цилиндра. Задачи. Круговой сектор. Найдите ординату точки A. Найдите площадь трапеции.

««Задачи по геометрии» 11 класс» — Ответим устно. Проблема. Около правильной шестиугольной призмы описана сфера радиуса 5 см. Призма. Многогранники, описанные около шара. Основанием треугольной пирамиды является прямоугольный треугольник. В правильную четырехугольную усеченную пирамиду вписан шар. Найдите радиус вписанной в правильную шестиугольную призму сферы. Измерения прямоугольного параллелепипеда. Технология проекта. Около треугольной призмы описана сфера, центр которой лежит вне призмы.

«Философ Пифагор» — Истина. Математика. Жизнь и научные открытия Пифагора. Слово «философ». Пифагор встречался с персидскими магами. Мнесарх. Основоположник современной математики. Пифагор. Девиз. Бессмертная идея. Мысль. Знание основ музыки. Египетские храмы. Направление полёта.

«Площадь сферы» — Радиус описанного шара равен половине диагонали куба: Диаметр шара (d=2R). Vш. сектора= 2/3ПR2h. Решение. Шаровой сектор состоит из шарового сегмента. описан шар. От данной точки (C). Тогда объем шара. раза больше площади поверхности большого круга. По построению радиусы шара и основания цилиндра равны. Объем шара радиуса. Равен. Радиус большого круга является радиусом шара. Высота сегмента (h). Сегмента = Пh2(R- 1/3h).

««Прямоугольный параллелепипед» геометрия» — Объем куба равен 64. Найдите объём многогранника. Найдите площадь поверхности многогранника. Формулы полной поверхности и объёма прямоугольного параллелепипеда. Все двугранные углы прямые. Прямоугольный параллелепипед. Прямоугольный параллелепипед в задачах В9 и В11 ЕГЭ. Найдите объём. Найдите квадрат расстояния между вершинами. Найдите угол CAD.

««Векторы» 11 класс» — История возникновения понятия вектор. Равенства. На рисунках вектор изображается отрезком со стрелкой. Вектор называется свободным, если его значение не меняется. Абсолютная величина вектора. Коллинеарные векторы. Сумма двух векторов. Примером скользящего вектора может служить сила. Пример. Векторы. Правило параллелограмма. Правило треугольника. Длиной или модулем ненулевого вектора АВ называется длина отрезка АВ.

Всего в теме «Геометрия 11 класс» 45 презентаций