Цилиндр: понятие, формула и секреты расчета площади поверхности в 11 классе

Что такое цилиндр

Разработка инженерных чертежей зданий, сооружений, оборудования начинается с самых простых фигур геометрии

Цилиндры применяют повсеместно, что объясняет важность умения рассчитывать их основные параметры, в том числе площадь. Цилиндром также называют классический головной убор

Цилиндрическую форму имеют трубы, архитектурные компоненты зданий, посуда, разнообразные резервуары.

Использование в производстве продукции именно такой формы позволяет значительно сократить затраты. К примеру, на изготовление сосуда в виде цилиндра уходит меньше материала, чем на выпуск аналогичных товаров в форме параллелепипеда. Это объясняется разницей в величинах площади боковой поверхности материального тела.

Цилиндрические предметы удобнее держать в руках и размещать в местах хранения. По этой причине бутыли с жидкостями разного состава, которые используют в медицине, салонах красоты и других сферах, имеют цилиндрическую форму. Многие химические вещества, в том числе, газы, агрессивные среды, нефтепродукты, масла, транспортируют в цистернах в виде цилиндров. Это связано с отсутствием уязвимых мест и максимальной герметичностью подобных резервуаров. В цилиндрической емкости центр тяжести находится ниже, чем в контейнере прямоугольной формы, что обеспечивает стабильность положения заполненного резервуара. Кроме того, давление на стенки цилиндра с жидкостью или газом распределяется более равномерно.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

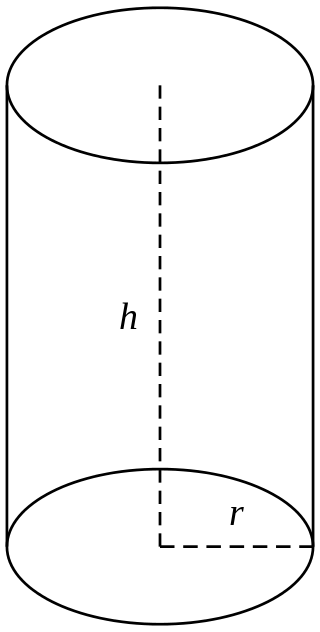
Цилиндром называют некое тело в геометрии, внутренние границы которого обозначены цилиндрической поверхностью и парой плоскостей, расположенных параллельно относительно друг друга и пересекающих эту поверхность.

Разберем основные понятия, с которыми часто сталкиваются школьники в процессе решения геометрических задач. К примеру, материальное тело обладает некой поверхностью

Величину площади этой поверхности важно знать для проведения вычислений в теории и на практике

Цилиндрическая поверхность представляет собой такую поверхность, которая сформирована с помощью параллельных прямых и некой кривой, называемой направляющей.

Цилиндр обладает основаниями, которые можно измерить. Они являются плоскими геометрическими фигурами. Для того чтобы получить основания, необходимо пересечь цилиндрическую поверхность парой плоскостей, расположенных параллельно по отношению друг к другу. Тот участок поверхности, который разделяет плоскости цилиндрических оснований, обозначают за боковую поверхность цилиндра. Плоскости оснований цилиндра высекают в своем перпендикуляре некий отрезок, называемый высотой цилиндра.

Существуют следующие виды цилиндров:

Прямой цилиндр с основаниями в виде кругов или эллипсов. В этом случае цилиндрическая ось расположена между центральными точками симметрии и является перпендикуляром к основаниям.
Косой цилиндр отличается от прямого геометрического тела расположением оси, то есть данный отрезок не перпендикулярен цилиндрическим основаниям.
Круговой цилиндр имеет направляющую в виде окружности.
Прямой круговой цилиндр (цилиндр вращения) получают в результате вращательного движения прямоугольника относительно какой-то стороны.
Эллиптический, параболический, гиперболический цилиндры названы так по форме основания, которые имеют вид эллипсов, парабол, гипербол соответственно. В случае параболического и гиперболического цилиндров объем измеряется бесконечностью.
Призма представляет собой цилиндр с основанием, которое обладает формой многоугольника.
Равносторонний цилиндр является таким цилиндром вращения, в котором наблюдается равенство диаметра основания и цилиндрической высоты.

Примечание 1

При параллельном расположении плоскостей основания и направляющей цилиндра форма границы данного основания идентична направляющей кривой.

Задача с прямым цилиндром

Покажем, как использовать полученные знания для решения следующей задачи. Пусть дан круглый прямой цилиндр. Известно, что осевое сечение цилиндра — квадрат. Чему равна площадь этого сечения, если всей фигуры составляет 100 см 2 ?

Для вычисления искомой площади необходимо найти либо радиус, либо диаметр основания цилиндра. Для этого воспользуемся формулой для общей площади S f фигуры:

Поскольку сечение осевое представляет собой квадрат, то это означает, что радиус r основания в два раза меньше высоты h. Учитывая это, можно переписать равенство выше в виде:

Теперь можно выразить радиус r, имеем:

Поскольку сторона квадратного сечения равна диаметру основания фигуры, то для вычисления его площади S будет справедлива следующая формула:

Мы видим, что искомая площадь однозначно определяется площадью поверхности цилиндра. Подставляя данные в равенство, приходим к ответу: S = 21,23 см 2 .

Стереометрия − это раздел геометрии, в котором изучаются фигуры в пространстве. Основными фигурами в пространстве являются точка, прямая и плоскость. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих существенных отличий стереометрии от планиметрии, так как во многих случаях задачи по стереометрии решаются путем рассмотрения различных плоскостей, в которых выполняются планиметрические законы.

В окружающей нас природе существует множество объектов, являющихся физическими моделями указанной фигуры. Например, многие детали машин имеют форму цилиндра или представляют собой некоторое их сочетание, а величественные колонны храмов и соборов, выполненные в форме цилиндров, подчеркивают их гармонию и красоту.

Греч. − кюлиндрос. Античный термин. В обиходе − свиток папируса, валик, каток (глагол − крутить, катать).

У Евклида цилиндр получается вращением прямоугольника. У Кавальери − движением образующей (при произвольной направляющей − «цилиндрика»).

Цель данного реферата рассмотреть геометрическое тело – цилиндр.

Для достижения данной цели необходимо рассмотреть следующие задачи:

− дать определения цилиндра;

− рассмотреть элементы цилиндра;

− изучить свойства цилиндра;

− рассмотреть виды сечения цилиндра;

− вывести формулу площади цилиндра;

− вывести формулу объема цилиндра;

− решить задачи с использованием цилиндра.

Нюансы расчета площади цилиндра

Расчет площади цилиндра, на первый взгляд, может показаться простым. Однако есть некоторые нюансы, которые стоит учитывать:

1. Убедитесь, что радиус и высота введены в одинаковых единицах измерения.

2. Учитывайте, что результат всегда зависит от точности введенных данных.

3. Помните, что цилиндрическая форма может иметь неровности или отклонения, которые нельзя учесть в простом расчете.

4. Проверьте ваши данные перед внесением в калькулятор.

5. Если у цилиндра нет одного из оснований (например, у стакана), площадь будет меньше.

6. В сложных задачах рекомендуется проводить расчеты вручную или с использованием специализированных программ.

7. При планировании использования материалов учитывайте запас, особенно при больших размерах цилиндра.

8. Помните о возможных деформациях при производстве или эксплуатации.

9. Расчеты могут не учитывать внутренние структуры или детали цилиндра.

10. Всегда доверяйтесь своему опыту и здравому смыслу.

Примеры для лучшего понимания

Давайте рассмотрим несколько примеров, чтобы лучше понять, как применять формулы для вычисления площади поверхности цилиндра:

Пример 1:

У нас есть цилиндр с радиусом основания 5 см и высотой 8 см. Какая будет площадь его поверхности?

1. Вычисляем площадь основания:

Площадь основания = π * 5^2 = 3.14159 * 25 = 78.54 см^2

2. Вычисляем площадь боковой поверхности:

Площадь боковой поверхности = 2 * π * 5 * 8 = 100.53 см^2

3. Вычисляем общую площадь поверхности:

Общая площадь поверхности = 2 * 78.54 + 100.53 = 257.61 см^2

Таким образом, площадь поверхности данного цилиндра составляет 257.61 см^2.

Пример 2:

У нас есть цилиндр с радиусом основания 3 м и высотой 10 м. Какая будет площадь его поверхности?

1. Вычисляем площадь основания:

Площадь основания = π * 3^2 = 3.14159 * 9 = 28.27 м^2

2. Вычисляем площадь боковой поверхности:

Площадь боковой поверхности = 2 * π * 3 * 10 = 188.50 м^2

3. Вычисляем общую площадь поверхности:

Общая площадь поверхности = 2 * 28.27 + 188.50 = 245.04 м^2

Таким образом, площадь поверхности данного цилиндра составляет 245.04 м^2.

Практическое применение вычисления площади поверхности цилиндра в реальной жизни

Привет друзья! Сегодня я хочу поговорить с вами о том, какое практическое применение может быть у знания о площади поверхности цилиндра в нашей реальной жизни. Мы рассмотрим примеры и задачи, где понимание этого понятия является весьма полезным.

Да, я знаю, что для кого-то математика может показаться скучной и никому не нужной, но поверьте мне, знание о площади поверхности цилиндра может найти свое применение в различных областях, таких как инженерия, архитектура, дизайн и даже в самых простых бытовых ситуациях. Позвольте мне объяснить, как это работает.

Секреты расчета объема цилиндра

Формула расчета объема цилиндра

В задачах по математике часто приходится сталкиваться с расчетом объема цилиндра. Для его определения используется следующая формула:

V — объем цилиндра
π — число пи (3,14…)
r — радиус цилиндра
h — высота цилиндра

Пример расчета объема цилиндра

Для лучшего понимания расчета объема цилиндра рассмотрим пример. Пусть у нас есть цилиндр с радиусом основания r = 3 см и высотой h = 8 см. Тогда объем цилиндра можно расчитать по формуле:

V = πr²h
V = 3,14 * 3² * 8	Подставляем известные значения
V ≈ 226,08	Рассчитываем значение

Таким образом, объем цилиндра составляет около 226,08 кубических сантиметров.

Полезные советы

Для удобства расчета можно использовать калькулятор или таблицу значений числа π
Проверьте правильность задания единиц измерения и диапазона значений радиуса и высоты цилиндра
Приблизительная оценка объема цилиндра может быть проведена путем сравнения с объемами простых фигур (куба, шара и т.п.)

Шаги по расчету площади цилиндра

Шаг 1: Измерьте высоту цилиндра. Это расстояние от основания до вершины цилиндра.

Шаг 2: Измерьте радиус основания цилиндра. Это расстояние от центра до края основания.

Шаг 3: Воспользуйтесь формулой для расчета площади боковой поверхности цилиндра: S = 2πr × h, где r — радиус основания, h — высота цилиндра, π ≈ 3,14.

Шаг 4: Рассчитайте площадь основания цилиндра. Для этого нужно воспользоваться формулой для площади круга: S = πr².

Шаг 5: Найдите общую площадь цилиндра. Для этого нужно сложить площадь боковой поверхности и две площади оснований: S = 2S_{основания} + S_{боковой поверхности}.

Примечание: если вам нужно найти объем цилиндра, то формула для расчета будет V = πr²h, где r — радиус основания, h — высота цилиндра, π ≈ 3,14.

Для чего может быть использован такой калькулятор?

Калькулятор площади цилиндра может быть использован в различных областях, где требуется расчет площади поверхности цилиндрических объектов. Некоторые из возможных применений калькулятора площади цилиндра включают:

Проектирование трубопроводов: при проектировании трубопроводов важно рассчитать не только объем жидкости или газа, но и площадь поверхности трубы, чтобы определить необходимое количество материала и затраты на изготовление трубопровода.

Производство бочек и цистерн: при производстве бочек и цистерн необходимо рассчитать площадь поверхности, чтобы правильно распределить материалы и обеспечить надежность конструкции.

Архитектура и строительство: при проектировании зданий, которые имеют цилиндрическую форму (например, башни, купола), необходимо рассчитать площадь поверхности, чтобы определить необходимое количество материалов для отделки или облицовки.

Образование: калькулятор площади цилиндра может быть полезен для студентов и учителей при изучении геометрии и тела вращения.

В целом, калькулятор площади цилиндра может использоваться в любой сфере, где требуется подсчет площади цилиндрических объектов.

Виды цилиндров

Прямой цилиндр – имеет одинаковые симметричные основания (круг или эллипс), параллельные друг другу. Отрезок между точками симметрии оснований перпендикулярен им, является осью симметрии и высотой фигуры.
Наклонный цилиндр – имеет одинаковые симметричные и параллельные друг другу основания. Но отрезок между точками симметрии не перпендикулярен этим основаниям.
Косой (скошенный) цилиндр – основания фигуры не взаимно параллельны.
Круговой цилиндр – основаниями является круг. Также выделяют эллиптические, параболические и гиперболические цилиндры.
Равносторонний цилиндр – прямой круговой цилиндр, диаметр основания которого равен его высоте.

Сами прямые называют образующими цилиндрической поверхности.
Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.

Так как все образующие и ось перпендикулярны плоскости альфа, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).

Если построить ещё одну плоскость бета, которая будет параллельна плоскости альфа, то отрезки образующих, заключённые между плоскостями альфа и бета будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости бета, дают окружность, равную окружности, лежащей в плоскости альфа.

Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях альфа и бета) называется цилиндром.
Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.

Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.

Сечения цилиндра различными плоскостями

Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого – образующие, а две другие – отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).

Основные формулы

Формула для вычисления площади боковой поверхности цилиндра: Sбок=2пRL.

То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: Sполн=2пR(R+L).

Примеры и разбор решения заданий тренировочного модуля

Дан цилиндр.

Выберите значение площади его боковой поверхности

60π
192π
120π
36π

Решение:

Площадь боковой поверхности вычисляется по формуле: S=2πRL.

R=6, L=10

Подставим: S=2π·6·10=120π.

Ответ: 3) 120π

Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.

Решение:

Sполн=2πR(R+L)

По условию задачи L=R+6.

144π=2πR(R+R+6).

Получили квадратное уравнение относительно радиуса:

R2+6R-72=0

R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.

Ответ: 12.

Задача

Осевое сечение цилиндра – квадрат со стороной 20 см. Найти высоту цилиндра, радиус цилиндра, ось цилиндра и площадь основания цилиндра.

Решение

Одна из сторон осевого сечения – образующая (она же равна оси цилиндра и она же равна высоте). Значит, высота и ось равны 20 см. Далее, вторая сторона осевого сечения – диаметр основания. Он равен 20 см, значит, радиус – 10 см. Наконец, площадь основания ищется по формуле

Итак, ребята, на этом уроке мы изучили, что такое цилиндрическая поверхность, её образующая; цилиндр, все его элементы и сечения; площади поверхностей цилиндра.

Широкое применение цилиндров в повседневной жизни

Цилиндр — это геометрическое тело, которое может использоваться в различных областях. Ниже приведены некоторые примеры использования цилиндра:

Создание двигателей внутреннего сгорания: таких как двигатель автомобиля или мотоцикла.
Механика: например в гидравлических цилиндрах, которые используются для перемещения или прессования тяжелых предметов.
Создание емкостей: таких как баки для хранения газа или жидкости.
Столярное дело: для создания столбов, колонн или других элементов архитектуры.
Математика: для решения геометрических задач и для вычисления объемов и площадей тел.
Кулинария: для формирования булочек, пирогов, кексов и других блюд.
Сосуды для хранения и транспортировки жидкостей: таких как газы, масла, смазки и прочее.
Научные исследования: например для измерения давления, температуры и других параметров.

Вопросы и ответы

Обратите внимание на ответы на некоторые часто задаваемые вопросы

Какова формула для вычисления площади цилиндра?

Формула для вычисления площади цилиндра зависит от того, какую площадь вы хотите найти. Обычно вычисляют площадь боковой поверхности и площадь полной поверхности цилиндра. Для нахождения площади боковой поверхности цилиндра используйте формулу 2πrh, где r — радиус цилиндра, а h — его высота. Для нахождения площади полной поверхности цилиндра нужно прибавить к площади боковой поверхности удвоенную площадь оснований, т.е. используйте формулу 2πrh + 2πr^2.

Как использовать онлайн калькулятор для вычисления площади цилиндра?

Чтобы использовать онлайн калькулятор для вычисления площади цилиндра, вам нужно ввести значения радиуса и высоты цилиндра в соответствующие поля. Затем онлайн калькулятор автоматически рассчитает площадь цилиндра.

Как найти радиус цилиндра, если известна его площадь?

Для нахождения радиуса цилиндра по известной площади необходимо использовать формулу S = 2πrh + 2πr^2, где S — площадь цилиндра, r — радиус цилиндра, h — его высота. После подстановки известных значений в формулу можно найти радиус цилиндра.

Нет, онлайн калькулятор площади цилиндра предназначен только для вычисления площади цилиндра. Для вычисления площади других геометрических фигур необходимо использовать соответствующие калькуляторы.

Онлайн калькулятор площади цилиндра не имеет ограничений на значения радиуса и высоты, которые можно ввести. Однако, для более точных результатов, рекомендуется использовать реалистичные значения.

Результаты вычислений, полученные с помощью онлайн калькулятора площади цилиндра, можно использовать для решения различных задач, связанных с геометрией, например, для расчета объема цилиндра, для определения необходимого количества материала для изготовления цилиндрического объекта или для определения количества жидкости, которая может поместиться в цилиндрический резервуар.

Боковая поверхность цилиндра

Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).

После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Верхнее основание исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.

Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.

Осевое сечение прямого цилиндра

Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.

В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.

Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.

Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:

Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.