Рассчитайте радиус цилиндра

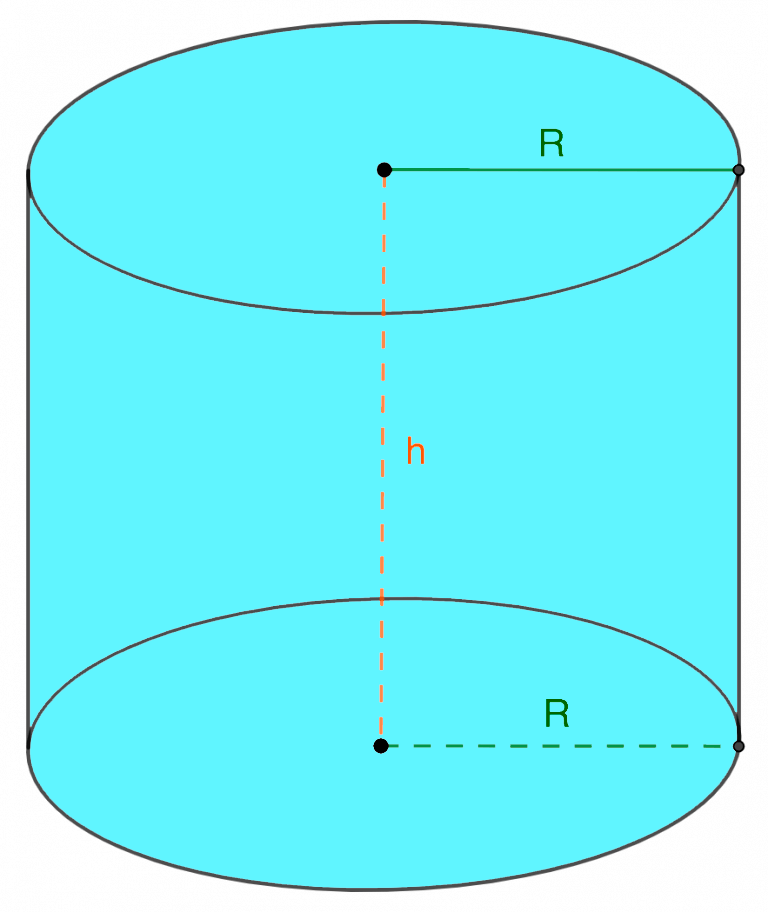
Определение диагонали осевого сечения

Диагональ осевого сечения имеет важную роль в различных инженерных и научных приложениях. Она используется для определения объема материала, помещающегося внутри цилиндра, и для расчета его площади поверхности. Архитекторы и дизайнеры могут использовать диагональ для размещения объектов внутри цилиндрического пространства с оптимальными параметрами.

Диагональ осевого сечения может быть измерена с помощью специальных инструментов, таких как линейка или измерительная лента. Для точного измерения необходимо определить начальную и конечную точки на внутренней поверхности цилиндра и учесть его радиус и длину.

Применение диагонали осевого сечения:	Описание
Расчет объема цилиндра	Диагональ осевого сечения позволяет определить объем материала, помещающегося внутри цилиндрической формы. Это может быть полезно при строительстве или производстве.
Расчет площади поверхности	Диагональ осевого сечения также используется для расчета площади поверхности цилиндра. Это может быть полезно при разработке упаковки или оценке необходимого материала для облицовки.
Размещение объектов	Архитекторы и дизайнеры могут использовать диагональ осевого сечения для оптимального размещения объектов внутри цилиндрического пространства, учитывая его размеры и форму.

В целом, диагональ осевого сечения — это важный концепт в геометрии и приложениях, связанных с цилиндрическими формами. Ее использование позволяет анализировать и измерять характеристики цилиндра для различных практических задач.

Практические рекомендации

Если необходимо найти диаметр основания цилиндра, следует воспользоваться формулой, которая связывает диаметр с радиусом и общей площадью основания: D = 2r = √(4S/π).

Для начала необходимо измерить общую площадь основания цилиндра. Это можно сделать с помощью рулетки или линейки. Если же основание имеет необычную форму, то можно воспользоваться формулами, позволяющими вычислить площадь треугольника, прямоугольника или многоугольника.

Затем следует вычислить радиус основания, разделив площадь на π и извлекая из полученного числа квадратный корень. Наконец, умножив радиус на 2, можно найти диаметр основания цилиндра.

Важно помнить, что все измерения должны быть проведены с высокой точностью, чтобы избежать ошибок в расчетах.
Если основание цилиндра имеет сложную форму, можно разбить его на более простые геометрические фигуры и вычислить площадь каждой из них отдельно.
Проверить правильность результатов можно, сравнив диаметр, найденный по формуле, с фактическим диаметром, полученным путем измерений.

Если возникают трудности в вычислении диаметра, можно воспользоваться онлайн калькулятором, который самостоятельно выполнит все необходимые расчеты и выведет результат на экран.

Вопрос-ответ

Вопрос: Как найти диаметр основания цилиндра, если известен объем?

Ответ: Для вычисления диаметра необходимо использовать формулу диаметра основания цилиндра по объему: d = 2 * √(V/πh), где d — диаметр, V — объем, h — высота цилиндра. Подставляем известные значения и получаем диаметр.

Вопрос: Как найти диаметр основания цилиндра, если известны его объем и высота?

Ответ: Для вычисления диаметра необходимо использовать формулу диаметра основания цилиндра по объему: d = 2 * √(V/πh), где d — диаметр, V — объем, h — высота цилиндра. Подставляем известные значения и получаем диаметр.

Вопрос: Как найти диаметр основания цилиндра, если известна площадь его боковой поверхности?

Ответ: Для вычисления диаметра необходимо использовать формулу диаметра основания цилиндра по боковой поверхности: d = 2 * h * (S/2πh), где d — диаметр, S — площадь боковой поверхности, h — высота цилиндра. Подставляем известные значения и получаем диаметр.

Вопрос: Как найти диаметр основания цилиндра, если известны его объем и радиус?

Ответ: Для вычисления диаметра необходимо использовать формулу диаметра основания цилиндра по радиусу и объему: d = 2 * (√(4V/π) — r), где d — диаметр, V — объем, r — радиус основания цилиндра. Подставляем известные значения и получаем диаметр.

Вопрос: Как найти диаметр основания цилиндра, если известны его площадь основания и высота?

Ответ: Для вычисления диаметра необходимо использовать формулу диаметра основания цилиндра по площади основания и высоте: d = √(4S/πh), где d — диаметр, S — площадь основания, h — высота цилиндра. Подставляем известные значения и получаем диаметр.

Главная — Онлайн — Новичкам в математике: как определить диаметр основания цилиндра без напряжения

Комментарии

JohnSmith

5.0 out of 5.0 stars5.0

Спасибо за быструю и понятную инструкцию! Теперь знаю, как найти диаметр основания цилиндра.

ChristopherDavis
5.0 out of 5.0 stars5.0

NikitaM
5.0 out of 5.0 stars5.0

Статья очень помогла, нашел ответ за 2 минуты. Спасибо!

Алексей
5.0 out of 5.0 stars5.0

Я всегда думал, что поиск диаметра основания цилиндра — это что-то сложно и запутанное. Но после того, как прочитал эту статью, мне стало все ясно. Спасибо за простую и доступную инструкцию. Теперь я смогу самостоятельно решить подобные задачи без проблем.

MichaelWilliams
5.0 out of 5.0 stars5.0

Сергей
5.0 out of 5.0 stars5.0

Я всегда считал, что математика — это не мое. И тем более, когда речь заходит об определении диаметра основания цилиндра — мне казалось, что это что-то сложное и запутанное. Тем не менее, после того, как я прочитал эту статью, я стал на много увереннее в своих способностях.

Рассмотренная в статье формула для расчета диаметра основания цилиндра оказалась настолько простой и понятной, что даже я в силах был ее освоить

Теперь я понимаю, что безумно важно не бояться новых задач и пробовать решать их самостоятельно

Спасибо авторам за качественный и доступный материал. Я считаю, что статьи такого формата помогают многим людям развиваться и учиться новому.

Площадь поперечного сечения

При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:S = πR 2

При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.

Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:

a 2 + b 2 = c 2

Из нее можно вывести такую формулу:

c = S*q*r*t*(a 2 + b 2 )

Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:

S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:

используется в тех случаях, когда сечение идет параллельно двум основаниям.

При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:

где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.

Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:

где 2а – значение хорды, расчета площади поперечного сечения.

Методы определения радиуса цилиндра

Существует несколько различных методов, которые можно использовать для определения радиуса цилиндра. Некоторые из них требуют использования специального оборудования, в то время как другие методы могут быть реализованы с помощью базовых измерительных инструментов.

1. Использование штангенциркуля

Один из наиболее распространенных методов измерения радиуса цилиндра — использование штангенциркуля. Этот инструмент позволяет производить измерения с высокой точностью.

Инструкции по измерению радиуса с использованием штангенциркуля:

Установите один характерный конец штангенциркуля на внешнюю поверхность цилиндра.
Осторожно подвигайте вторым концом штангенциркуля по поверхности цилиндра, пока не будет достигнут максимальный размер. Запишите показание шкалы.
Установите один конец штангенциркуля на внутреннюю поверхность цилиндра.
Осторожно подвигайте вторым концом штангенциркуля, пока не будет достигнут минимальный размер

Запишите показание шкалы.

Радиус цилиндра можно рассчитать, вычтя показания шкалы измерений внутреннего и внешнего радиуса. Радиус равен половине разности между внешним и внутренним радиусами.

2. Использование шнурка и линейки

Другой простой метод для определения радиуса цилиндра — использование шнурка и линейки. Этот метод особенно полезен, когда штангенциркуль или другие точные измерительные инструменты недоступны.

Инструкции по измерению радиуса с использованием шнурка и линейки:

1. Оберните шнурок полностью вокруг цилиндра вдоль его максимального диаметра.
2. Отметьте начальную точку на шнурке.
3. Снимите шнурок с цилиндра и расположите его на линейке.
4. Измерьте длину от начальной точки до отметки на шнурке.

Радиус цилиндра можно рассчитать, разделив измеренную длину на 2π (или около 6,28) — пр

Формулы цилиндра

А если это прямоугольник, то мы знаем, как найти площадь. Нам нужно умножить длину на высоту. Так мы получим площадь боковой поверхности цилиндра.

(S_{сторона} = 2 pi RH)

В этой формуле 2R — длина окружности основания, где R — его радиус, а H — образующая (или высота) цилиндра. Подробнее о площади прямоугольника и длине окружности (а также о площади круга) вы можете прочитать в статьях «Параллелограмм» и «Окружность и окружность».

Мы нашли площадь боковой поверхности. Как найти общую площадь поверхности?

Для этого нужно сложить площади боковой поверхности и оснований. Таким образом, мы получаем следующую формулу.

(S = S_{сторона} + 2S_{основание} = 2 pi RH+2 pi R^2 = 2 pi R(H + R))

Допустим, мы решили заварить чашку очень вкусного чая, но чтобы его правильно заварить, нам нужно знать точное количество воды. Для этого рассчитаем объем цилиндра. Воспользуемся следующей формулой:

(V = S_{main}H = pi R^2H)

В этой формуле R — радиус цилиндра, H — высота.

Часто формулу объема можно использовать для решения жизненных задач. Например, чтобы найти объем детали, погруженной в воду.

Пример 1. В цилиндрическую емкость наливают 1650 см3 жидкости. Часть была утоплена в этом судне. При этом уровень жидкости увеличился в 1,2 раза. Найдите объем детали. Выразите ответ в см3.

Решение.

Шаг 1. Выразите высоту жидкости в первый и второй раз. Предположим, что изначально уровень жидкости был равен х, затем после погружения в него детали стал равен 1,2х.

Шаг 2. Вспомним физику и заметим, что объем жидкости в сосуде после погружения в него детали будет равен сумме объемов жидкости и детали: V = Vl + Vd.

Шаг 3. Через объем жидкости выражаем площадь дна сосуда:

Вж = Прим.Ч
1650 = Собаза.x
(S_{основной} = frac{1650}{x})

Шаг 4. Подставляем площадь основания в формулу объема жидкости после погружения в нее детали:

(V = S_{main}H = frac{1650}{x} * 1,2x = 1980)

Шаг 5. Тогда объем детали будет равен:

Vд = V — Вж
Генеральный директор = 1980 — 1650 = 330

Ответ: 330 см3

Объем цилиндра. Площадь боковой поверхности цилиндра.Площадь полной поверхности цилиндра

      Для цилиндра с   r   и   h   (рис. 5)

Рис.5

введем следующие обозначения

V	объем цилиндра
Sбок	площадь
Sполн	площадь
Sосн	площадь

      Тогда справедливы следующие формулы для вычисления объема, площади :

S_осн = πr2,

V = S_оснh = πr2h,

S_бок= 2πrh,

S_полн = 2πr2 + 2πrh == 2π(r + h).

      Замечание 7. Формула объема цилиндра   V = πr2h   может быть получена из

при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Почему важно знать длину окружности основания цилиндра

В строительстве и архитектуре знание длины окружности основания цилиндра позволяет расчетно определить необходимое количество материалов для облицовки поверхности цилиндрических столбов, колонн или колоннад. Зная длину окружности основания, можно правильно подобрать материалы и минимизировать затраты. Также, зная эту величину, можно рассчитать объем и массу цилиндрического сооружения.

В области механики и техники знание длины окружности основания цилиндра позволяет определить периметр и площадь сечения цилиндра. Эти характеристики, в свою очередь, необходимы для расчета силы воздействия на стенки цилиндра, его прочности и устойчивости

Знание длины окружности основания также важно для анализа тепло- и гидродинамики цилиндрических трубопроводов

В науке и исследованиях знание длины окружности основания цилиндра помогает в решении различных геометрических задач, а также представляет собой базовую информацию для более сложных вычислений и моделирования. Эта величина может быть использована при изучении свойств материалов, определении геометрических параметров объектов и естественных явлений.

Таким образом, знание длины окружности основания цилиндра является неотъемлемой частью различных сфер деятельности, где геометрические величины играют важную роль. Правильное и точное определение этой величины позволяет достичь оптимальных результатов и избежать ошибок при проведении расчетов и измерений.

Ошибка, которую нужно избегать при расчете диагонали цилиндра

При расчете диагонали цилиндра очень важно не допустить ошибки, которая может привести к неправильному результату. Одной из распространенных ошибок является использование неправильной формулы для расчета диагонали цилиндра

Некоторые люди ошибочно считают, что диагональ цилиндра равна сумме диаметра и высоты. Однако, это неверно

Одной из распространенных ошибок является использование неправильной формулы для расчета диагонали цилиндра. Некоторые люди ошибочно считают, что диагональ цилиндра равна сумме диаметра и высоты. Однако, это неверно.

Правильная формула для расчета диагонали цилиндра выглядит следующим образом:

диагональ = √(диаметр² + высота²)

Главное, чтобы использовать правильные значения диаметра и высоты цилиндра в этой формуле. Неправильные измерения или смешение между диаметром и радиусом могут привести к неверному результату.

Поэтому, перед расчетом диагонали цилиндра, убедитесь, что вы правильно определили значения диаметра и высоты, а также использовали правильную формулу для расчета. Это поможет избежать ошибок и получить точный результат.

Важные моменты при расчете диагонали цилиндра

1. Знание формулы для расчета диагонали: Для определения диагонали цилиндра необходимо использовать формулу, основанную на свойствах прямоугольного треугольника. Формула выглядит следующим образом: диагональ = корень квадратный из (высоты^2 + радиус^2).

2. Измерение высоты и радиуса: Для получения точных значений высоты и радиуса цилиндра необходимо использовать правильные методы измерения. Высоту можно измерить с помощью линейки или мерной ленты, удерживая ее параллельно оси цилиндра. Радиус можно измерить с помощью штангенциркуля, учитывая его центральное положение относительно оси цилиндра.

3

Правильное округление результата: Получив значение диагонали цилиндра по формуле, важно правильно округлить результат. Округлять нужно в соответствии с требованиями задачи или стандартами, учитывая необходимое количество десятичных знаков

4. Проверка расчетов: Необходимо проверить полученный результат, проведя расчеты еще раз или с помощью других методов. Это поможет исключить возможные ошибки и убедиться в достоверности полученного значения диагонали.

Учитывая все эти важные моменты, можно гарантировать точность и корректность расчета диагонали цилиндра, что позволит использовать его результаты в дальнейших вычислениях и применениях.

Метод измерения диаметра

Для измерения диаметра цилиндра можно использовать различные инструменты, такие как штангенциркуль, микрометр или измерительную ленту

Важно учесть, что выбор инструмента зависит от размеров цилиндра и требуемой точности измерения

Прежде чем производить измерение диаметра, необходимо убедиться, что поверхность цилиндра, по которой будет проходить измерение, в достаточно хорошем состоянии. Наличие царапин, неровностей или других дефектов может привести к неточности результатов измерений.

Перед измерением необходимо также установить цилиндр в горизонтальное положение, чтобы диаметр измерялся в плоскости, перпендикулярной оси цилиндра. Это поможет избежать искажений результатов измерений, связанных с наклоном цилиндра.

При использовании штангенциркуля для измерения диаметра следует приложить один его ниблер к одной точке на поверхности цилиндра, а другой ниблер — к противоположной точке

Затем нужно осторожно снять штангенциркуль и считать значения на шкале. Разность между этими значениями будет соответствовать диаметру цилиндра

В случае использования микрометра измерение диаметра производится аналогично: одну его измерительную головку следует прижать к одной точке цилиндра, а вторую головку — к точке диаметрально противоположной. Разница между показаниями микрометра будет соответствовать диаметру цилиндра.

Если в распоряжении есть измерительная лента, можно обернуть ее вокруг цилиндра, проходящего через его диаметр, и затем прочитать длину отрезка, соответствующего диаметру. Полученное значение будет равно диаметру цилиндра.

Важно помнить, что при измерении диаметра необходимо быть внимательным и аккуратным, чтобы получить наиболее точные результаты. Использование правильных инструментов и правильная техника измерений помогут достичь этой цели

Что такое цилиндр?

У цилиндра есть несколько важных характеристик. Диаметр цилиндра — это расстояние между точками, лежащими на противоположных границах его оснований, проходящее через его центр. Высота цилиндра — это расстояние между его основаниями.

Цилиндр часто встречается в реальной жизни, например, в виде банки, столба или колонны. Его геометрические свойства и формулы, связанные с его рассчетами, широко применяются в инженерии, архитектуре, физике и других областях науки. Понимание основных понятий и свойств цилиндра позволяет упростить и ускорить расчеты и построение моделей на практике.

Способы вычисления длины окружности цилиндра

Длина окружности цилиндра представляет собой меру периметра его основания, которая может быть рассчитана с использованием различных формул. Вот несколько способов вычисления длины окружности цилиндра:

1. Формула длины окружности:

Длина окружности цилиндра может быть вычислена, зная радиус основания (r) или диаметр основания (d), с помощью формулы:

л = 2πr

или

л = πd

2. Формула периметра основания:

Длина окружности цилиндра также может быть вычислена с использованием формулы периметра основания, если известны высота цилиндра (h) и длина стороны основания (l), с помощью формулы:

л = 2(периметр основания)

где

периметр основания = l = 2πr (для круглого основания) или

периметр основания = l (для многоугольного основания)

3. Приближенный метод с использованием нити:

Для приближенного определения длины окружности цилиндра можно использовать метод с использованием нити. В этом методе нить обвивается вокруг цилиндра вдоль периметра основания, а затем измеряется длина нити с использованием линейки или ленты. Однако такой метод будет иметь определенную погрешность измерения, поскольку нить может быть натянута неоднородно или не облегать окружность точно.

При вычислении длины окружности цилиндра важно учитывать единицы измерения, такие как сантиметры, метры или дюймы, и приводить ответ в правильной форме и точности

Виды цилиндров

1. Прямой цилиндр – имеет одинаковые симметричные основания (круг или эллипс), параллельные друг другу. Отрезок между точками симметрии оснований перпендикулярен им, является осью симметрии и высотой фигуры.
2. Наклонный цилиндр – имеет одинаковые симметричные и параллельные друг другу основания. Но отрезок между точками симметрии не перпендикулярен этим основаниям.
3. Косой (скошенный) цилиндр – основания фигуры не взаимно параллельны.
4. Круговой цилиндр – основаниями является круг. Также выделяют эллиптические, параболические и гиперболические цилиндры.
5. Равносторонний цилиндр – прямой круговой цилиндр, диаметр основания которого равен его высоте.

Сами прямые называют образующими цилиндрической поверхности.
Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.

Так как все образующие и ось перпендикулярны плоскости альфа, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).

Если построить ещё одну плоскость бета, которая будет параллельна плоскости альфа, то отрезки образующих, заключённые между плоскостями альфа и бета будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости бета, дают окружность, равную окружности, лежащей в плоскости альфа.

Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях альфа и бета) называется цилиндром.
Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.

Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.

Сечения цилиндра различными плоскостями

Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого – образующие, а две другие – отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).

Основные формулы

Формула для вычисления площади боковой поверхности цилиндра: Sбок=2пRL.

То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: Sполн=2пR(R+L).

Примеры и разбор решения заданий тренировочного модуля

Дан цилиндр.

Выберите значение площади его боковой поверхности

1. 60π
2. 192π
3. 120π
4. 36π

Решение:

Площадь боковой поверхности вычисляется по формуле: S=2πRL.

R=6, L=10

Подставим: S=2π·6·10=120π.

Ответ: 3) 120π

Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.

Решение:

Sполн=2πR(R+L)

По условию задачи L=R+6.

144π=2πR(R+R+6).

Получили квадратное уравнение относительно радиуса:

R2+6R-72=0

R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.

Ответ: 12.

Задача

Осевое сечение цилиндра – квадрат со стороной 20 см. Найти высоту цилиндра, радиус цилиндра, ось цилиндра и площадь основания цилиндра.

Решение

Одна из сторон осевого сечения – образующая (она же равна оси цилиндра и она же равна высоте). Значит, высота и ось равны 20 см. Далее, вторая сторона осевого сечения – диаметр основания. Он равен 20 см, значит, радиус – 10 см. Наконец, площадь основания ищется по формуле

Итак, ребята, на этом уроке мы изучили, что такое цилиндрическая поверхность, её образующая; цилиндр, все его элементы и сечения; площади поверхностей цилиндра.

Решение задачи нахождения осевого сечения

Для решения задачи нахождения осевого сечения цилиндра, квадрат диагональ которого равна 10, необходимо использовать базовые геометрические принципы. Осевое сечение представляет собой плоскость, которая пересекает цилиндр параллельно его оси.

Пусть сторона квадрата, образующего осевое сечение, равна a. Так как диагональ квадрата равна 10, то по теореме Пифагора получаем a^2 + a^2 = 10^2. Приводим уравнение к виду 2a^2 = 100 и делим обе части на 2: a^2 = 50. Извлекаем квадратный корень из обеих частей уравнения и получаем a ≈ 7,07.

Итак, сторона квадрата, образующего осевое сечение цилиндра, примерно равна 7,07.

Таким образом, задача нахождения осевого сечения решена. Для этого были применены базовые геометрические принципы, а именно использование теоремы Пифагора и извлечение квадратного корня.

Как найти осевое сечение цилиндра квадрат, диагональ которого равна 10?

Для решения данной задачи необходимо знать, как найти осевое сечение цилиндра. Осевое сечение цилиндра представляет собой пересечение плоскости и цилиндра, которая проходит через его ось.

Для определения осевого сечения цилиндра квадрат, диагональ которого равна 10, необходимо учесть, что диагональ квадрата является линией, соединяющей две противоположные вершины. В данном случае, длина диагонали равна 10, что означает, что сторона квадрата равна 10/√2, поскольку квадрат является прямоугольным треугольником со сторонами 10 и 10.

Таким образом, осевое сечение данного цилиндра будет представлять собой квадрат с диагональю, равной 10 и стороной, равной 10/√2.

Нахождение радиуса цилиндра

Для решения данной задачи, где известна диагональ квадрата, который является осевым сечением цилиндра и равен 10, необходимо использовать геометрические свойства и формулы для нахождения радиуса цилиндра.

Первым шагом следует определить длину стороны квадрата, которая равна диагонали, разделенной на √2. Таким образом, получаем значение стороны квадрата равное 10/√2.

Радиус цилиндра может быть найден как половина длины стороны квадрата. Для этого необходимо разделить значение стороны квадрата на 2: 10/(√2 * 2).

Итак, радиус цилиндра равен 5/√2 или (5√2)/2, что можно упростить до (5√2)/2.

• Известно: диагональ квадрата — 10
• Требуется найти: радиус цилиндра

Шаги решения:

1. Находим длину стороны квадрата: 10/√2
2. Находим радиус цилиндра: (10/√2)/2 = (5√2)/2

Таким образом, радиус цилиндра, основанного на заданном осевом сечении квадрата с диагональю 10, составляет (5√2)/2.

Что такое диагональ цилиндра

Расчет диагонали цилиндра является важным элементом для понимания геометрических свойств этой фигуры и его применения в различных областях. Для расчета диагонали цилиндра используется формула, которая зависит от параметров цилиндра, таких как радиус основания и высота.

Знание диагонали цилиндра может быть полезным при проектировании и строительстве, а также при решении задач, связанных с объемом и площадью поверхности цилиндра.

Изучение диагонали цилиндра поможет лучше понять его геометрические свойства и использовать это знание в решении практических задач, связанных с данной фигурой.

Определение диаметра

Диаметр основания цилиндра является одним из основных параметров фигуры, поскольку он определяет ее размер и объем. Определить диаметр можно по различным формулам в зависимости от известных значений.

Если известен радиус цилиндра, то диаметр можно вычислить по формуле: d = 2r, где d — диаметр, r — радиус. Данную формулу можно использовать, если в задаче дан радиус или длина окружности.

Если известен объем цилиндра и высота, то диаметр можно вычислить по формуле: d = 2√(V/πh), где d — диаметр, V — объем, h — высота. Указанную формулу можно использовать, если в задаче даны объем и высота.

Также есть формула для определения диаметра по площади поверхности цилиндра и высоте: d = 2√(S/πh), где d — диаметр, S — площадь поверхности, h — высота. Эту формулу можно использовать, если в задаче дана площадь поверхности и высота.

• Для вычисления диаметра основания цилиндра необходимо знать либо радиус, либо объем, либо площадь поверхности фигуры.
• Существует несколько формул для вычисления диаметра в зависимости от данных, которые известны.
• Вычисление диаметра основания цилиндра является важным этапом решения задач, связанных с фигурами трехмерного пространства.