Цилиндр, его элементы и виды цилиндров
Наиболее распространенным видом цилиндра в геометрии является прямой круговой цилиндр. Введем его определение.
По определению понятно, почему в некоторых случаях эту фигуру называют цилиндром вращения.
На рисунке выше изображен цилиндр, который является результатом вращения прямоугольника АВСD вокруг оси, обозначенной О1О2. Поворот происходит на 180°. Аналогичный итог получаем, если повернуть ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.
Перечислим ключевые элементы цилиндра:
- Основания цилиндра в виде пары идентичных по габаритам и площади круга с центральными точками, обозначенными за О1 и О2.
- R определяет радиус, который имеют основания геометрической фигуры.
- AD и BC являются диаметрами (d) оснований цилиндра.
- O1O2 представляет собой ось симметрии рассматриваемого цилиндра, а также играет роль его высоты (h).
- l (AB, CD) в виде образующих цилиндра являются сторонами прямоугольника ABCD, которые соответствуют высоте геометрической фигуры.
Представим изображение развертки цилиндра:
Заметим справедливость следующих соотношений:
- рассматриваемый прямоугольник имеет длину, равную длине окружности основания цилиндра ;
- ширина соответствует высоте (образующей) цилиндра.
Геометрическая фигура в виде цилиндра может обладать следующими видами сечений:
1. Осевое сечение имеет прямоугольную форму, сформировано при пересечении цилиндра плоскостью, которая пролегает через ее ось. На примере первого рисунка осевым сечением является АВСD. Определить площадь данного сечения легко, достаточно умножить высоту цилиндра на диаметр его основания.
2. Сечение в виде прямоугольника образуется в том случае, когда секущая плоскость не пересекает ось фигуры, но расположена перпендикулярно по отношению к основаниям цилиндра.
3. Сечение в виде аналогичного основаниям цилиндра круга образовано при условии параллельности секущей плоскости основаниям рассматриваемой фигуры.
4. При пересечении цилиндра плоскостью, которая не является параллельной его основаниям и не пересекается с ними, образуется сечение в виде эллипса.
5. Сечение в виде параболы и гиперболы сформировано путем пересечения секущей плоскости с одним из оснований цилиндра.
Рассмотрим основные виды цилиндров с примерами, которые часто встречаются на уроках в классе. Сначала разберемся с понятием прямого цилиндра.
Данная фигура обладает идентичными основаниями, расположенными симметрично и параллельно, в виде круга или эллипса. Отрезок, соединяющий точки симметрии оснований, является перпендикуляром к этим основаниям, осью симметрии и равен высоте фигуры.
Наклонный цилиндр обладает идентичными основаниями, которые расположены параллельно относительно друг друга. Отрезок, соединяющий точки симметрии, не перпендикулярен к основаниям фигуры.
Косой, или скошенный, цилиндр отличается расположением оснований. В данном случае они расположены не параллельно друг другу.
В круговом цилиндре основания имеют форму кругов.
Существуют также такие разновидности цилиндров:
- эллиптические;
- параболические;
- гиперболические.
Равносторонний цилиндр представляет собой прямой круговой цилиндр с основанием, диаметр которого соответствует высоте фигуры.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.
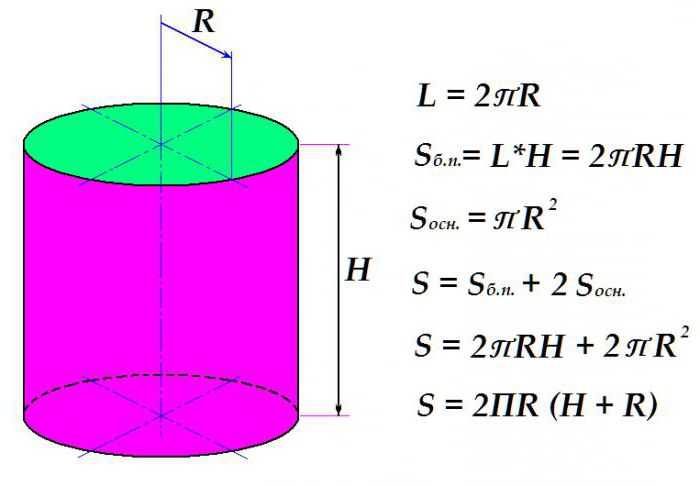
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П
на радиус окружности.
Площадь круга, как известно, равняется произведению П
на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Примеры расчета площади осевого сечения цилиндра
Для вычисления площади осевого сечения цилиндра необходимо знать его радиус и высоту. Вот несколько примеров расчета площади осевого сечения цилиндра:
Пример 1:
Радиус цилиндра: 5 см
Высота цилиндра: 10 см
Формула для расчета площади осевого сечения цилиндра:
S = π * r * r
где S — площадь осевого сечения, π — математическая константа (примерное значение 3.14), r — радиус цилиндра.
Расчет:
- Подставляем значения в формулу: S = 3.14 * 5 * 5 = 78.5 см²
- Площадь осевого сечения цилиндра равна 78.5 см².
Пример 2:
Радиус цилиндра: 8 см
Высота цилиндра: 15 см
Формула для расчета площади осевого сечения цилиндра:
S = π * r * r
где S — площадь осевого сечения, π — математическая константа (примерное значение 3.14), r — радиус цилиндра.
Расчет:
- Подставляем значения в формулу: S = 3.14 * 8 * 8 = 200.96 см²
- Площадь осевого сечения цилиндра равна 200.96 см².
Пример 3:
Радиус цилиндра: 12 см
Высота цилиндра: 20 см
Формула для расчета площади осевого сечения цилиндра:
S = π * r * r
где S — площадь осевого сечения, π — математическая константа (примерное значение 3.14), r — радиус цилиндра.
Расчет:
- Подставляем значения в формулу: S = 3.14 * 12 * 12 = 452.16 см²
- Площадь осевого сечения цилиндра равна 452.16 см².
Таким образом, площадь осевого сечения цилиндра может быть вычислена с использованием формулы S = π * r * r, где S — площадь осевого сечения, π — математическая константа (примерное значение 3.14), r — радиус цилиндра.
«Компоненты» стереометрической фигуры
Цилиндр состоит из нескольких составляющих.
- Цилиндрическая поверхность — это поверхность, которая образуется большим количеством параллельных прямых, проходящих через точки некоторой кривой.
- Основания — это плоские фигуры, которые образованы пересечением ЦП с двумя параллельными плоскостями, ограничивающими цилиндр. Оснований у цилиндра два.
- Боковой поверхностью называют часть ЦП, которая находится между основаниями.
- И, наконец, высота — это отрезок, который высекается плоскостями оснований цилиндра на прямой, перпендикулярной им.
Примечание
Дополнительно можно измерить периметр Sбок. Для этого нужно длину окружности l сложить с высотой h и умножить данную сумму на 2.
Рассмотрим, как различаются типы рассматриваемой геометрической фигуры по форме. Цилиндр может быть:
- Прямой. Его основания имеют центры симметрии, то есть являются кругами или эллипсами. При этом прямая между центрами перпендикулярна плоскостям оснований. Данная прямая называется осью цилиндра.
- Косой. Его основания имеют центры симметрий, однако отрезок между ними не перпендикулярен плоскостям оснований.
- Круговой. Имеет окружность в роли направляющей.
- Прямой круговой. Его можно получить с помощью вращения прямоугольника вокруг одной из его сторон. Тогда эта сторона будет осью цилиндра и осью симметрии.
- Равносторонний. Его диаметр равен высоте.
- Эллиптический, гиперболический и параболический. Образованы соответственно эллипсами, гиперболами и параболами.
- Усеченный. Геометрическое тело, которое отсекается от цилиндра плоскостью, не параллельной основанию.
- Призма. Является разновидностью цилиндра, если имеет основание в виде многоугольника.
Понятие цилиндра
Цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью (боковая поверхность цилиндра) и двумя параллельными плоскостями (основаниями цилиндра).
Основание цилиндра — это круглая плоскость, на которую опирается геометрическая фигура. Таких оснований у цилиндра 2, они абсолютно одинаковы.
Прямая, соединяющая центры оснований, называется осью цилиндра. Плоскость, проходящая через ось будет осевым сечением. Очень часто данное понятие возникает при решении задач ЕГЭ. На рисунке ниже выделено красным пунктиром.
Вся боковая поверхность цилиндра состоит из бесконечного количества прямых, параллельных оси цилиндра. Эти прямые носят название образующих цилиндра. На рисунке выше это AB или KD.
Высотой цилиндра является длина его образующей, а радиус основания — радиусом цилиндра.
Основные формулы для вычисления боковой и полной площади
Кроме рабочих способов, перечисленных выше, рассчитать площадь рассматриваемого тела можно следующими методами:
- Через диаметр и высоту: \( S_{полн.}=D\times\pi\left(h+\frac D2\right); S_{бок.}=D\times\pi\times h.\)
- Через объем: \(S=\frac Vh.\)
- Через длину окружности. Так как \(l=2\times\pi\times R\), то \(S_{бок.}=l\times h\), а \(S_{полн.}=l\times h+2\times\pi\times R^2\).
Приведем примеры расчета.
Задача 1
Радиус основания цилиндра равен 2, высота равна 3. Высчитать площадь боковой поверхности цилиндра.
Решение
\(S_{бок.}=2\times\pi\times R\times h\)
Из этого: \(S_{бок.}=2\times3,14\times2\times3=6,28\times6=37,68.\)
Ответ: \(S_{бок.}=37,68.\)
Задача 2
\(S_{бок.}=24\pi\), а диаметр основания — 3. Узнать высоту цилиндра.
Решение
\(S_{бок.}=2\times\pi\times R\times h\)
Высоту отсюда вычислим так:
\(h=\frac{S_{бок.}}{2\pi R}\)
Радиус равен: \(R=\frac D2. h=\frac{24\pi}{2\pi\times0,5D}=\frac{24\pi}{2\pi\times0,5\times3}=\frac{12}{1,5}=8\)
Решение задач на тему «Цилиндр»
Пример 1 (Ященко 36 вариантов, 2021 год, вариант 10)
В цилиндрическом сосуде уровень жидкости достигает 25 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2,5 раза больше диаметра первого? Ответ дайте в см.
Решение: Раз переливают жидкость, значит это задача на объём.
Но при этом наши объёмы равны, жидкость то одна.
Раз по условию диаметр второго сосуда в 2,5 раза больше, значит и радиус изменяется так же. Но тут нужно учесть «подвох» — радиус в формуле у нас возведён в квадрат. Вспоминая правило пропорции, считаем:
Ответ: 4
Пример 2 (Ященко 36 вариантов, 2021 год, вариант 26)
В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 6. Боковые рёбра призмы равны . Найдите объём цилиндра, описанного около этой призмы.
Решение: для нахождения объёма цилиндра, нам нужен радиус основания и высота. Но боковые рёбра призмы будут равны высоте цилиндра, раз по условию цилиндр описан около этой призмы. Значит, нужно посчитать только радиус основания.
В основании призмы прямоугольный треугольник. А мы знаем, что в таком случае, гипотенуза будет лежать на диаметре окружности. Значит, для нахождения радиуса нужно найти гипотенузу и поделить её на 2.
Воспользуемся теоремой Пифагора. Наши катеты 5 и 6:
Значит, радиус будет равен:
Ну и находим объём цилиндра:
Ответ: 61
Пример 3
Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен R, его высота — Н, а расстояние между прямой АВ и осью цилиндра равно D. Найдите Н, если R=10, D=8, АВ=13.
Решение:
Как найти основание цилиндра
Основание цилиндра является плоскостью, на которую цилиндр опирается и которая образует его верхнюю и нижнюю плоскости. Основание цилиндра представляет собой круг, и его площадь можно рассчитать по формуле:
| Формула для площади основания цилиндра: |
|---|
| S = πr2, |
| где S — площадь основания, r — радиус основания. |
Для подсчета площади основания цилиндра необходимо знать радиус основания. Радиус — это расстояние от центра круга (основания) до любой точки его границы. Если вам известен радиус этого круга, просто возведите его в квадрат и умножьте на число Пи (π) — примерно равное 3,14159.
- Сначала определите радиус основания цилиндра.
- Затем возведите радиус в квадрат.
- Умножьте полученное значение на число Пи.
Теперь у вас есть площадь основания цилиндра!
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.
Примечания
Wikimedia Foundation
.
2010
.
Синонимы
Смотреть что такое «Цилиндр» в других словарях:
— (лат. cylindrus) 1) геометрическое тело, ограниченное с концов двумя кругами, с боков плоскостью, огибающею эти круги. 2) в часовом мастерстве: особого рода рычаг двойного колеса. 3) шляпа, имеющая форму цилиндра. Словарь иностранных слов,… … Словарь иностранных слов русского языка
цилиндр
— а, м. cylindre m., нем. Zylinder <, лат. cylindrus <гр. 1. Геометрическое тело, образуемое вращение прямоугольника вокруг одной из его сторон. Объем цилиндра. БАС 1. Толстота цилиндра равна площади его основанья, помноженной на высоту. Даль … Исторический словарь галлицизмов русского языка
Муж., греч. прямая стопка, вал; облец, обляк; тело, ограниченное с концов двумя кругами, а с боков гнутою по кругам плоскостью. Толстота цилиндра равна площади его основанья, помноженной на высоту, геом. Паровой цилиндр, халява, труба, в которой… … Толковый словарь Даля
— высокая мужская шляпа из шелкового плюша с небольшими твердыми полями … Большой Энциклопедический словарь
ЦИЛИНДР, твердое тело или поверхность, образуемые вращением прямоугольника вокруг одной из его сторон в качестве оси. Объем цилиндра, если обозначить его высоту как h, а радиус основания как r, равен pr2h, а площадь изогнутой поверхности 2prh … Научно-технический энциклопедический словарь
ЦИЛИНДР, цилиндра, муж. (от греч. kylindros). 1. Геометрическое тело, образуемое вращением прямоугольника около одной из его сторон, называемой осью, и имеющее в основаниях круг (мат.). 2. Часть машин (двигателей, насосов, компрессоров и т.д.) в… … Толковый словарь Ушакова
ЦИЛИНДР, а, муж. 1. Геометрическое тело, образованное вращением прямоугольника вокруг одной из его сторон. 2. Колонновидный предмет, напр. часть поршневой машины. 3. Высокая твёрдая шляпа такой формы с небольшими полями. Чёрный ц. | прил.… … Толковый словарь Ожегова
— (Steam cylinder) одна из основных деталей поршневых машин. Выполняется в виде полого круглого Ц., в котором движется поршень. Ц. паровых машин снабжается обычно паровой рубашкой для обогревания его стенок в целях уменьшения конденсации пара.… … Морской словарь
Цилиндр
Опр.
Цилиндром называется тело, которое состоит из двух кругов, совмещаемых
параллельным переносом и всех отрезков, соединяющих соответствующие точки
этих кругов.
Круги называют основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей этих кругов – образующими цилиндра (рис. 1)
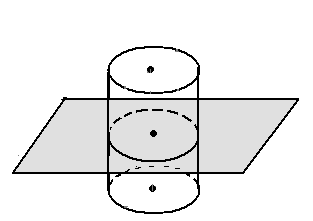
рис. 1 рис. 2 рис. 3 рис. 4
Свойства цилиндра:
1) Основания цилиндра равны и лежат в параллельных плоскостях.
2) Образующие цилиндра равны и параллельны.
Опр.
Радиусом цилиндра называется радиус его основания.
Опр.
Высотой цилиндра называется расстояние между плоскостями его оснований.
Опр.
Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
Осевое сечение цилиндра – прямоугольник со сторонами 2R
и l
(в прямом цилиндре l
= Н) рис. 2
Сечение цилиндра, параллельные его оси, являются прямоугольниками (рис. 3).
Сечение цилиндра плоскостью, параллельной основаниям – круг, равный основаниям (рис. 4)
Площадь поверхности цилиндра.
Боковая поверхность цилиндра составлена из образующих.
Полная поверхность цилиндра состоит из оснований и боковой поверхности.
S
полн
= 2
S
осн
+
S
бок
;
S
осн
=
П
∙
R
2
;
S
бок
= 2
П
∙
R
∙Н
S
полн
= 2П
R
∙(R
+ Н)
Практическая часть:
№1.
Радиус цилиндра равен 3см, а его высота- 5см. Найдите площадь осевого сечения и площадь пол-
ной поверхности цилиндра.
№2.
Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 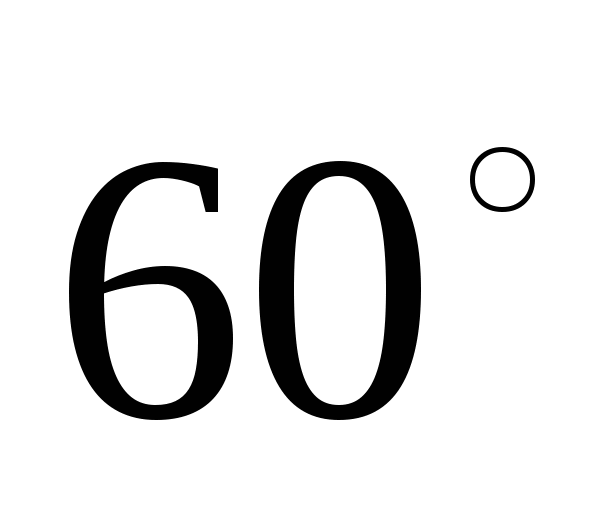 и равна 20 см. Найдите площадь боковой поверхности цилиндра.
и равна 20 см. Найдите площадь боковой поверхности цилиндра.
№3.
Радиус цилиндра равен 2см, а его высота- 3см. Найдите диагональ осевого сечения цилиндра.
№4.
Диагональ осевого сечения цилиндра, равная 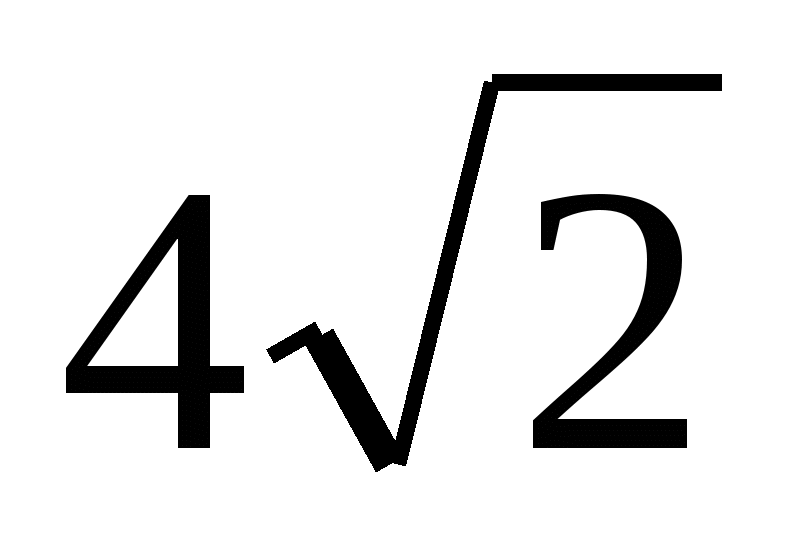 , образует с плоскостью основания угол
, образует с плоскостью основания угол  . Найдите площадь боковой поверхности цилиндра.
. Найдите площадь боковой поверхности цилиндра.
№5.
Площадь боковой поверхности цилиндра равна 15 . Найдите площадь осевого сечения.
. Найдите площадь осевого сечения.
№6.
Найдите высоту цилиндра, если площадь его основания равна 1, а S
бок =  .
.
№7.
Диагональ осевого сечения цилиндра имеет длину 8см и наклонена к плоскости основания под углом 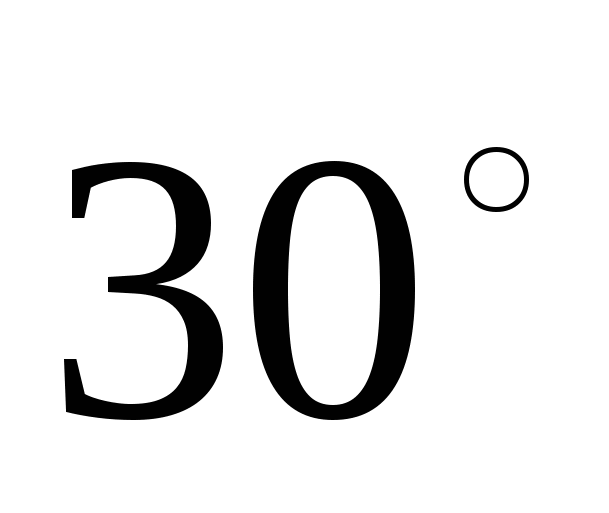 . Найдите полную поверхность цилиндра.
. Найдите полную поверхность цилиндра.
Цилиндрическая дымовая труба с диаметром 65см имеет высоту 18м. Сколько жести нужно для её изготовления, если на заклепку уходит 10% материала?
Связанные определения
Цилиндрическая поверхность
— поверхность, получаемая при движении прямой (образующей), параллельной какой-либо заданной, пересекающей кривую линию (направляющую), лежащую в не параллельной заданной прямой плоскости.
Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями называются основаниями цилиндра
.
Цилиндрическая поверхность между плоскостями оснований называется боковой поверхностью
цилиндра.
В случае параллельности плоскости основания и плоскости направляющей, граница основания будет по форме совпадать с направляющей.
Пример 2: Осевое сечение цилиндра в машиностроении
В машиностроении осевые сечения цилиндра широко используются для создания различных деталей и механизмов. Один из типичных примеров применения осевых сечений цилиндра в машиностроении — это создание поршней для двигателей внутреннего сгорания.
Осевые сечения цилиндра используются для определения формы и размеров поршневой камеры, которая является одной из ключевых частей двигателя. Оптимальная форма поршневой камеры позволяет обеспечить эффективное сжатие топливовоздушной смеси, что в свою очередь улучшает производительность двигателя и снижает выбросы.
Процесс создания поршня с осевым сечением цилиндра включает несколько этапов. Сначала определяют необходимые параметры: диаметр цилиндра и ход поршня. Затем задают требуемый объем поршневой камеры и желаемые характеристики сжатия. На основе этих данных создается модель поршня, включающая осевое сечение цилиндра.
С использованием модернизированных техник и передовых расчетных методов осевое сечение цилиндра может быть оптимизировано для достижения требуемых целей проектирования. Для этого могут применяться различные материалы и нанесение специальных покрытий на поверхность поршня, чтобы улучшить его теплоотвод и износостойкость.
Примеры использования осевых сечений цилиндра в машиностроении также включают создание цилиндрических труб для гидравлических и пневматических систем, а также различных стержней и валов для передачи движения в механизмах.
Использование осевых сечений цилиндра в машиностроении — это важный инструмент для проектирования и изготовления деталей и механизмов с заданными характеристиками и функциональностью. Оптимальная форма и размеры осевых сечений цилиндра позволяют улучшить работу механизмов и обеспечить их долговечность и надежность в эксплуатации.
Пример 1: Осевое сечение цилиндра в строительстве
Осевое сечение цилиндра – это геометрическая фигура, которая получается при пересечении цилиндра плоскостью, проходящей через его ось. Данное понятие широко применяется в строительстве для проектирования и расчета различных конструкций.
Одним из примеров применения осевого сечения цилиндра в строительстве является проектирование и расчет арочных мостов. Цилиндрическая форма арки позволяет обеспечить максимальную прочность конструкции при минимальном использовании материалов. Для этого основание арки делается в виде осевого сечения цилиндра, а плоскость поперечного сечения, в которой заключена арка, параллельна оси цилиндра.
При проектировании арочных мостов необходимо учитывать осевые силы, возникающие в арке. Осевые силы – это силы, направленные вдоль оси цилиндра. Их расчет осуществляется с использованием осевого сечения цилиндра, так как оно позволяет определить форму арки и ее геометрические характеристики, такие как радиус кривизны и высоту.
Осевое сечение цилиндра также находит применение при проектировании баков и резервуаров для хранения жидкостей или газов. Это позволяет определить объем и форму бака, а также рассчитать его прочность и устойчивость.
Как найти радиус цилиндра
Радиус цилиндра является одной из основных характеристик этой геометрической фигуры. Чтобы найти радиус цилиндра, необходимо знать хотя бы одно из следующих значений: площадь осевого сечения, объем или высоту цилиндра. В данном разделе мы рассмотрим способы нахождения радиуса цилиндра при известных значениях площади осевого сечения и объема.
Нахождение радиуса по площади осевого сечения
Если известна площадь осевого сечения цилиндра, то радиус можно найти, используя следующую формулу:
Радиус = √(Площадь / π)
Где π (пи) — математическая константа, приблизительно равная 3,14.
Нахождение радиуса по объему
Если известен объем цилиндра, то радиус можно найти, используя следующую формулу:
Радиус = √(Объем / (π * Высота))
Где π (пи) — математическая константа, приблизительно равная 3,14.
Таким образом, зная площадь осевого сечения или объем цилиндра, а также зная его высоту, можно легко найти радиус. Не забывайте использовать соответствующую формулу в зависимости от известных данных.
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
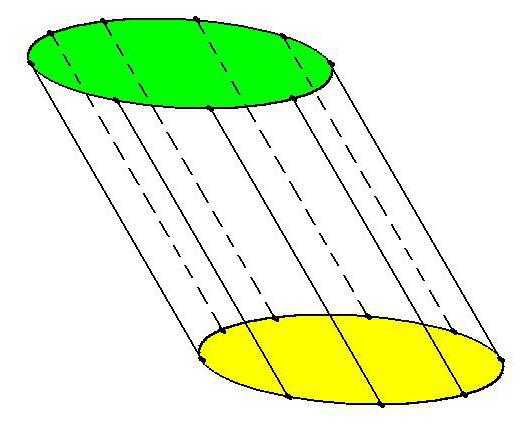
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
Связанные определения
Цилиндрическая поверхность
— поверхность, получаемая при движении прямой (образующей), параллельной какой-либо заданной, пересекающей кривую линию (направляющую), лежащую в не параллельной заданной прямой плоскости.
Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями называются основаниями цилиндра
.
Цилиндрическая поверхность между плоскостями оснований называется боковой поверхностью
цилиндра.
В случае параллельности плоскости основания и плоскости направляющей, граница основания будет по форме совпадать с направляющей.
Как найти площадь осевого сечения цилиндра
Осевое сечение цилиндра — это плоскость, пересекающаяся с цилиндром и разделяющая его на две части. Площадь осевого сечения является одним из важных параметров цилиндра и может быть полезной при решении различных задач.
Для расчета площади осевого сечения цилиндра необходимо знать его радиус и высоту. Существуют два основных типа осевых сечений:
и круглое сечение и овальное сечение.
Круглое сечение
Для круглого осевого сечения цилиндра формула для расчета площади будет:
Площадь = π * r^2
- π — математическая константа, примерное значение которой равно 3.14159.
- r — радиус осевого сечения.
Пример:
Если радиус осевого сечения цилиндра равен 5 см, то его площадь будет:
Площадь = 3.14159 * (5 см)^2 = 78.54 см^2.
Овальное сечение
Для овального осевого сечения цилиндра формула для расчета площади будет более сложной, так как ее форма может варьироваться. В таком случае требуется измерить длину и ширину овального сечения. Площадь осевого сечения цилиндра можно вычислить по формуле:
Площадь = длина * ширина
Пример:
Допустим, что длина овального осевого сечения цилиндра равна 10 см, а ширина — 6 см. Тогда площадь сечения будет:
Площадь = 10 см * 6 см = 60 см^2.
Другие типы осевых сечений
Кроме круглого и овального осевых сечений цилиндра, могут существовать и другие формы сечений, такие как треугольные, прямоугольные, многоугольные и т. д. Для этих типов сечений также вам понадобятся измерения соответствующих сторон и углов для определения их площади.
Важно помнить, что измерения осевого сечения цилиндра должны быть выполнены с достаточным уровнем точности для получения корректных результатов
Площадь цилиндра — как правильно рассчитать
Определение
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.
Перед тем, как начать вычисление площади цилиндра, необходимо учесть, что существует два ее вида:
- Полная площадь поверхности цилиндра. Она равна сумме боковой поверхности цилиндра и двойной площади его основания.
- Площадь боковой поверхности цилиндра. Она равняется произведению высоты цилиндра на длину окружности основания.
Чтобы вычислить общую площадь поверхности цилиндра, нужно применить формулу:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
\(S=2\times\pi\times R\times h+2\times\pi\times R^2=2\times\pi\times R\times\left(h+R\right)\)
Здесь R — радиус окружности, а h — высота.
Чтобы найти площадь боковой поверхности цилиндра, нужно воспользоваться формулой:
\(S=2\times\pi\times R\times h\)






























