Калькулятор объема цилиндра

Круглый прямой цилиндр

Пусть директрисой будет окружность некоторого радиуса. Тогда образованная генератрисой фигура будет называться круглым цилиндром. Тем не менее генератриса относительно плоскости, ограниченной директрисой, может быть направлена произвольным образом. Поэтому в общем случае говорят о наклонном круглом цилиндре. Если же генератриса будет перпендикулярна плоскостям основания, то цилиндр называется прямым. Он показан на рисунке ниже.

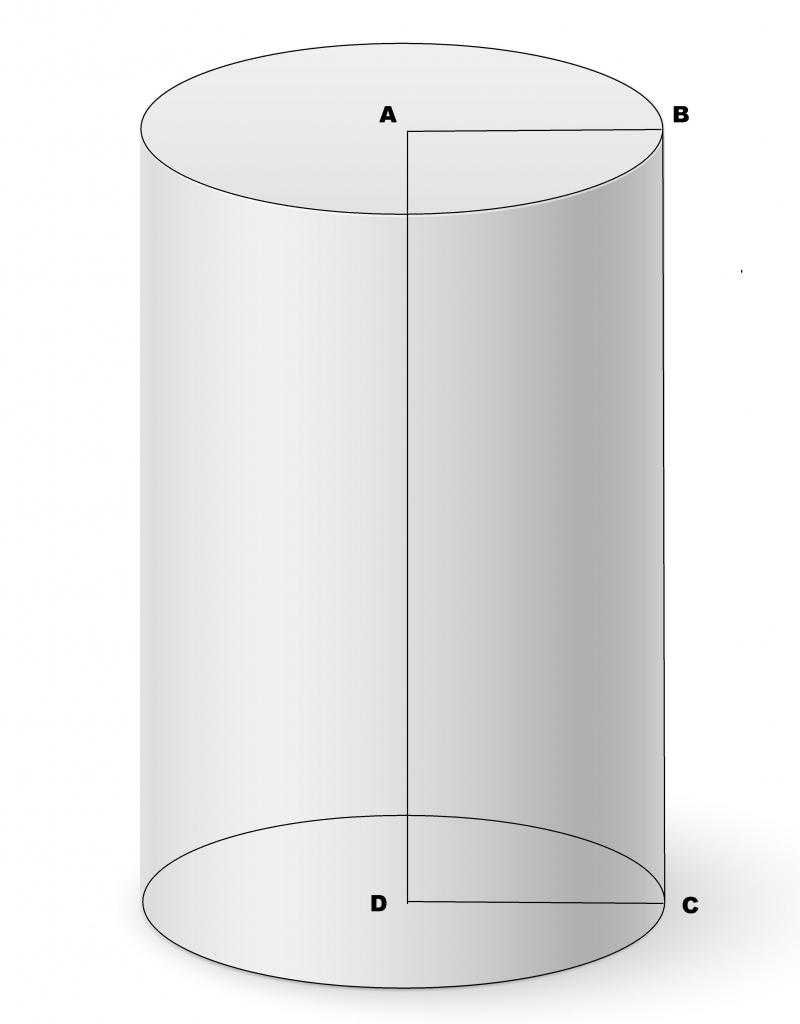
Здесь AB = DC — радиус цилиндра, AD = BC = h — высота фигуры. Для прямого цилиндра высота всегда равна длине образующей. Отрезок AD обозначает ось цилиндра — прямая, соединяющая две центральные точки оснований. От оси цилиндра все точки боковой поверхности лежат на одном расстоянии, равном радиусу фигуры.

Далее в статье будем рассматривать развертку поверхности цилиндра, круглого и прямого.

Объем пирамиды

Для начала рассмотрим треугольную пирамиду. Вершину пирамиды примем за начало координат точку О, а ось Ох проведем перпендикулярно основанию, причем ось будет направлена от вершины пирамиды к основанию.

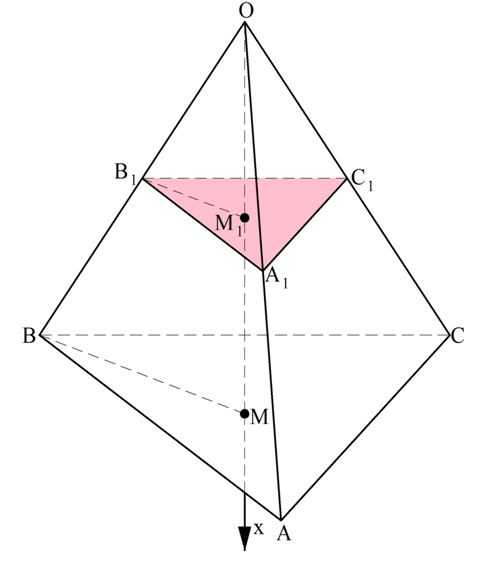
Пусть ось Ох пересечет основание АВС в точке М. Тогда ОМ – это высота, чью длину мы обозначим как h.

Далее построим сечение А₁В₁С₁, параллельное АВС. Это сечение пересечется с ОМ в точке ОМ₁. Тогда ОМ₁ – это координата х, характеризующая расположение сечения А₁В₁С₁.

Осталось составить выражение для площади ∆А₁В₁С₁. Так как АВ||A₁B₁, то ∠АВО и ∠А₁В₁О одинаковы как соответственные углы. Тогда у ∆АВО и ∆А₁В₁О есть два равных угла (ведь ∠АОВ у них общий), а потому эти треугольники подобны по первому признаку подобия. Это означает, что

Надо как-то найти значение коэффициента k, который, очевидно, как-то зависит от переменной х. Рассмотрим теперь ∆ОМВ и ∆ОМ₁В₁. Они прямоугольные, ведь ОМ перпендикулярен плоскостям этих треугольников. Также у них есть общий угол ∠ОВМ. Значит, они подобны, и поэтому

Итак, если пирамида имеет высоту h и площадь основания S, то объем пирамиды равен:

Выведенная нами формула справедлива для треугольной пирамиды. Однако если в основании пирамиды лежит произвольный многоугольник, то, разбив этот многоугольник на треугольники, мы разобьем и пирамиду на несколько треугольных пирамид. У них будет общая высота h и площади оснований S₁, S₂, S₃…, которые в сумме составляют площадь многоугольника S.

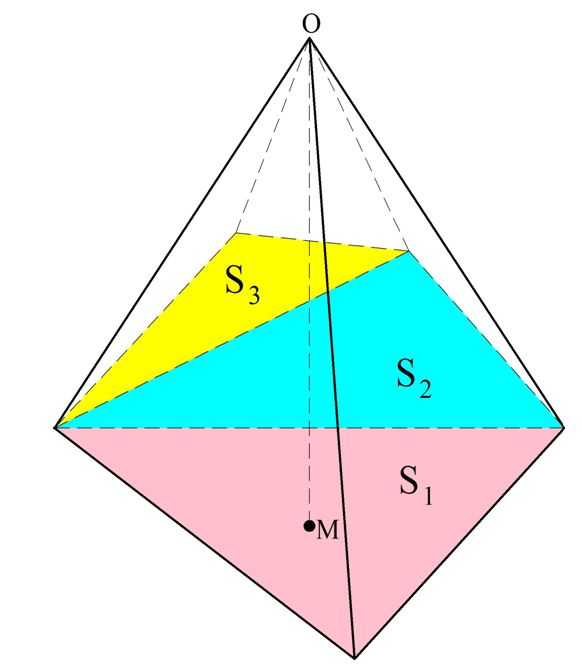
Объем треугольных пирамид рассчитывается по выведенной нами формуле:

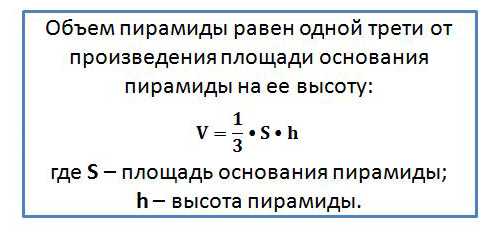
Задание. В основании пирамиды высотой 15 лежит квадрат со стороной 4. Вычислите ее объем.

Решение. Сначала находим площадь основания. Для этого надо сторону квадрата умножить саму на себя:

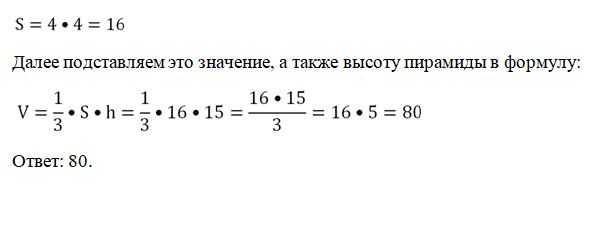
Задание. В кубе АВСDA₁В₁С₁D₁ отмечены точки Е и F – середины ребер ВС и CD соответственно. Во сколько раз объем пирамиды С₁EFC меньше объема куба?

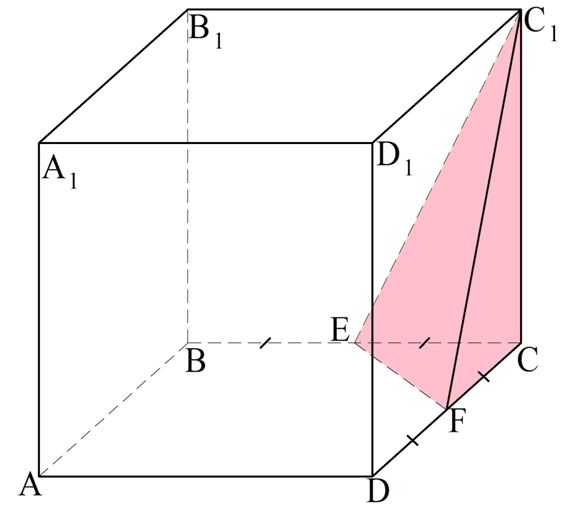
Решение. Обозначим длину ребра куба буквой а. Тогда его объем рассчитывается так:

Задание. Отрезок MN перпендикулярен плоскости пятиугольника АВСDE. Точка K, принадлежащая этой плоскости, делит отрезок MN в отношении 2:1. Во сколько раз объем пирамиды MABCDE больше объема пирамиды NABCDE?

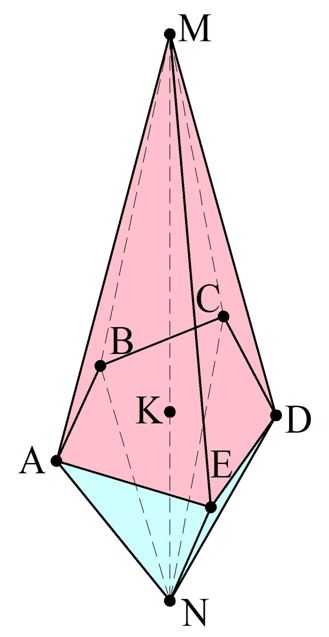
Решение. Запишем формулы для объемов этих пирамид. При этом учтем, что MK – высота для MABCDE, а NK – это высота для NABCDE.

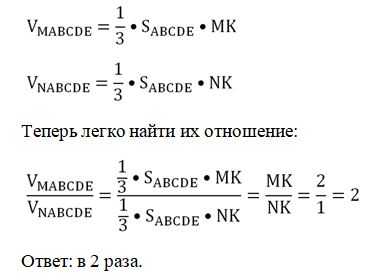
Далее рассмотрим такую фигуру, как усеченная пирамида. Ясно, что ее объем можно вычислить, если из объема исходной пирамиды вычесть объем отсеченной верхушки.

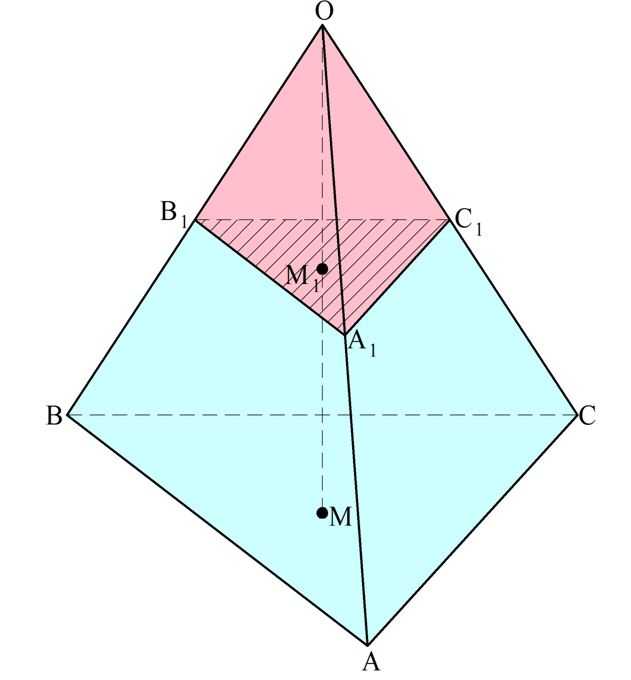
Снова рассмотрим пирамиду ОАВС, через которую проведено сечение А₁В₁С₁, параллельное основанию.

Обозначим площадь нижнего основания пирамиды как S₂, а площадь верхнего основания – как S₁. Далее высоту усеченной пирамиды (отрезок ММ₁) обозначим как h. Мы уже выяснили ранее, что основания АВС и А₁В₁С₁ – это подобные треугольники, причем коэффициент их подобия k равен отношению высот ОМ и ОМ₁. Тогда можно записать:

Далее используем основное свойство пропорции:

Далее числитель дроби мы раскладываем на множители, используя формулу разности кубов:

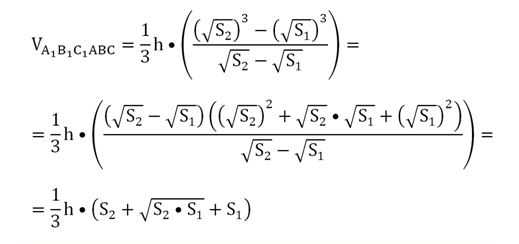
Задание. Основаниями усеченной пирамиды являются квадраты со сторонами 9 см и 5 см, а высота пирамиды составляет 6 см. Найдите ее объем.

Сначала вычислим площади оснований:

Обозначения

• R — радиус основания цилиндра;
• D — диаметр основания цилиндра;
• h — средняя высота усечённого цилиндра;
• h1 — наименьшая высота усечённого цилиндра;
• h2 — наибольшая высота усечённого цилиндра;
• α — угол сечения, град.
• X_{1 .. n} — координаты для построения развёртки по оси X;
• Y_{1 .. n} — координаты для построения развёртки по оси Y;

Числовые значения в таблице заполняются числом (5; 5.16; -3.12), либо математическим выражением (5/7; (1-5)*2.13)

Введите высоты * и (или) угол:

Без макс. и мин. высоты можно посчитать только площади боковой поверхности и основания и объём

Или введите одну из высот и угол сечения (рис.)

Шаровой сегмент

Когда плоскость проходит через шар, она рассекает его на две фигуры, которые именуются шаровым сегментом. Если из центра шара О провести радиус ОА длиной R в направлении плоскости сечения, который перпендикулярен этой плоскости, то он пересечет ее какой-то точке В. Длину отрезка АВ называют высотой шарового сегмента и обозначают буквой h:

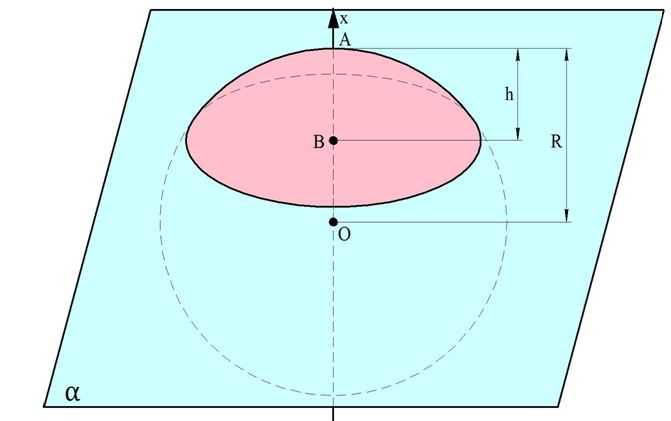
Ясно, что при этом отрезок ОВ – это расстояние от секущей плоскости (или от основания сегмента) до центра шара, причем этот отрезок имеет длину R –h.

Можно считать, что шаровой сегмент, как и шар, получается при вращении дуги окружности вокруг оси Ох. Однако если сам шар при этом ограничен плоскостями x = R и х = – R, то сегмент ограничен другими плоскостями: х = R и х = R – h. Это значит, что его объем можно вычислить с помощью интеграла также, как и объем шара, отличаться будет лишь нижний предел интегрирования:

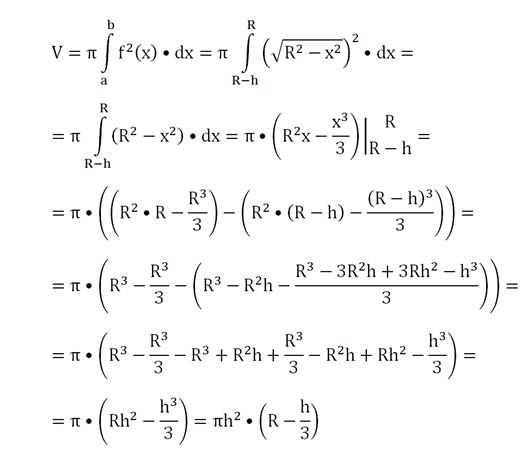
Заметим, что шар можно рассматривать как шаровой сегмент, чья высота вдвое больше его радиуса. И действительно, если в выведенную формулу мы подставим значение h = 2R, то получим уже известную нам формулу объема шара.

Задание. Найдите объем шарового сегмента высотой 6, если он отсечен от шара радиусом 15.

Решение. Используем выведенную формулу:

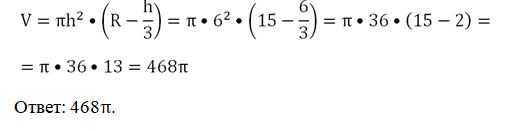
Задание. Диаметр шара разделили на три равных отрезка. Через концы этих отрезков провели секущие плоскости, перпендикулярные диаметру. Чему равен объем тела, заключенного между этими двумя плоскостями (оно называется шаровым слоем), если радиус шара обозначен буквой R?

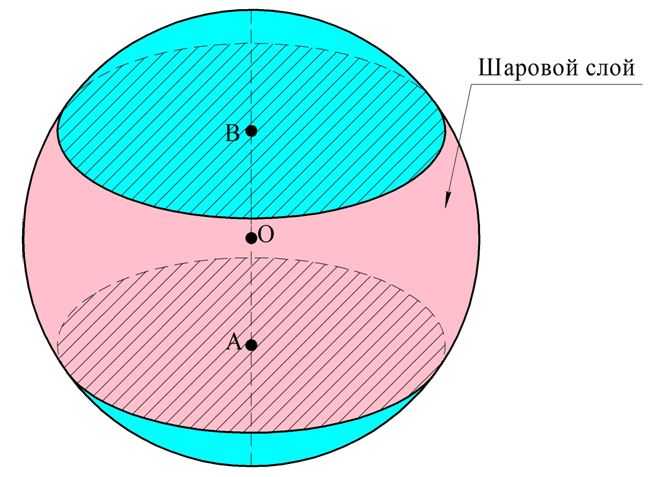
Решение. Ясно, что для вычисления объема шарового слоя достаточно вычесть из объема шара объемы двух шаровых сегментов, образующихся при проведении секущих плоскостей. Так как они разделили диаметр на три одинаковых отрезка, то высота этих сегментов будет в три раза меньше диаметра шара:

Площадь развертки цилиндра

Выше мы показали, как можно получить развертку фигуры. Чтобы рассчитать ее площадь, необходимо сложить площади для всех ее частей, то есть для двух круглых оснований и одного прямоугольника.

Обозначим радиус основания буквой r, а высоту фигуры — буквой h. Площадь одного основания равна площади круга, то есть:

S_o = pi*r2

Здесь pi — число Пи, приблизительно равное 3,14.

Чтобы вычислить площадь прямоугольника, представляющего боковую поверхность фигуры в развернутом виде, необходимо знать две его стороны. Одна из них равна высоте h. Вторая, как можно догадаться, соответствует длине директрисы, то есть длине окружности. Обозначим ее l. Тогда можно записать следующие равенства:

l = 2*pi*r;

S_b = l*h = 2*pi*r*h

Здесь S_b — площадь прямоугольника, равная площади цилиндрической поверхности.

Учитывая, что фигура имеет два основания, складываем рассчитанные величины, получаем общую площадь развертки цилиндра:

S = 2*S_o + S_b = 2*pi*r2 + 2*pi*r*h = 2*pi*r*(r + h)

Площадь S фигуры однозначно определяется через ее радиус и высоту.

Покажем, как использовать это равенство для решения геометрической задачи.

Что такое усеченный цилиндр?

Усеченный круговой цилиндр, также известный как цилиндрический сегмент, представляет собой твердое тело, образованное пропусканием непараллельной плоскости через круговой цилиндр. Некруглое верхнее основание наклонено к круглому сечению. Если круговой цилиндр является правильным цилиндром, то каждая правая часть представляет собой круг, имеющий такую ​​же площадь, что и основание.

Пусть K — площадь правого сечения, а h ₁ и h _{2 —} самый короткий и самый длинный элемент усеченного цилиндра соответственно. Объем усеченного кругового цилиндра определяется формулой, приведенной ниже. Если усеченный цилиндр представляет собой правильный круговой цилиндр радиуса r, объем можно выразить через радиус.

V = K

V = πr 2

Усеченные цилиндры

Джон Рэй Куэвас

Вычисление объёма

Довольно часто для работы с цилиндрами требуется вычислить его объём. Это процедура в последнее время производится с применением вычислительной техники. Однако, чтобы провести такую процедуру необязательно использовать калькулятор и другие дополнительные методы решения поставленной задачи.

Сейчас существует несколько основных методов, которые позволяют произвести вычисление данного параметра. Это, по сути, универсальные формулы. Каждая из таких формул имеет свои входные параметры, отталкиваясь от которых и можно найти требуемое значение объёма. Это позволяет достигнуть ряда положительных моментов в расчётах.

1. Значительно сокращается время для осуществления операций подсчёта объёма.
2. Уменьшается вероятность того что может быть совершена ошибка в расчётах
3. Требуется для вычисления ограниченное число параметров, знание которых и даёт возможность достигать результата.

Методы расчёта

Существует два основных метода, которые позволяют производить вычисление такого параметра.

1. Метод вычисления объёма цилиндра на основе высоты геометрической фигуры. Этот метод является универсальным средством и может быть использован для фигур любого типа как прямоугольных, так и наклонных цилиндров. Дополнительно к значению высоты в данном способе следует знать и площадь основания. Если остановиться подробнее на данном параметре, то надо отметить что основанием является круг. Поэтому вычисление площади круга происходит на основе радиуса. Таким образом, вторым параметром в данном методе должен выступать радиус основания цилиндра. Тогда площадь определяется согласно стандартной формуле.

S= П *R^2

В данной формуле принято следующее обозначение при помощи переменных:

• П – это параметр, обозначающий соотношение между длиной и радиусом окружности, равный 3,1415928.
• R – Радиус окружности, лежащий в основании цилиндра.
• S — Площадь основания фигуры.

Вычисление непосредственно объёма цилиндра производится на основе стандартной формулы.

V=S*h

В данной формуле принято следующее обозначение при помощи переменных:

• S – Площадь основания цилиндра, имеющего форму круга.
• h – Высота геометрической фигуры.
• V – объём цилиндра.

1. Вторым методом, позволяющим произвести вычисление объёма данной фигуры, является соотношение таких параметров, как высота цилиндра и радиуса его основания. По сути, данная формула является преобразованной формулой первого метода. В ней нет разделения на промежуточные этапы подсчёта параметров. Сразу же включены все математические операции.

Таким образом, в ней одновременно производится подсчёт площади круга и объёма цилиндра.

Приведём формулу расчёта объёма цилиндра для данного метода.

V= П *R^2*h

В данной формуле принято следующее обозначение при помощи переменных:

• П – это параметр, обозначающий соотношение между длиной и радиусом окружности, равный 3,1415928.
• R – Радиус окружности, лежащий в основании цилиндра.
• h – Высота геометрической фигуры.
• V – Объём цилиндра.

Как работает онлайн-калькулятор объема цилиндра

Сегодня многие задачи можно решить с помощью интернет-сервисов, и онлайн-калькулятор объема цилиндра – отличный пример. Чтобы правильно вычислить объем цилиндра, используется простая формула: V = π * r^2 * h, где π (пи) — математическая константа, приблизительно равная 3,14, r — радиус основания цилиндра, а h — его высота.

1. Ввод данных: В первую очередь, пользователь должен внести необходимые параметры: диаметр (или радиус) и высоту цилиндра. Эти параметры могут быть представлены в различных единицах измерения: метрах, сантиметрах или миллиметрах.
2. Обработка информации: Как только данные введены, калькулятор автоматически применяет формулу для вычисления объема. Этот процесс занимает считанные миллисекунды.
3. Результат: Пользователь получает ответ в кубометрах, кубических сантиметрах или других единицах, в зависимости от исходных данных.

Преимущества использования онлайн-калькулятора

• Точность расчетов. Шанс ошибиться при ручном расчете гораздо выше, чем при использовании автоматизированной системы, особенно для тех, кто редко сталкивается с подобными вычислениями.
• Быстрота. Время, потраченное на ввод параметров и получение результата, составляет всего несколько секунд, в то время как ручной расчет может занять гораздо больше времени.
• Доступность. Необходимость рассчитать объем цилиндра может возникнуть в любом месте и в любое время. Благодаря онлайн-калькулятору это возможно даже через смартфон.
• Многозадачность. Большинство современных калькуляторов также предоставляют дополнительные функции, такие как вычисление площади поверхности цилиндра или его боковой поверхности.
• Образовательный аспект. Использование онлайн-калькулятора может быть полезным инструментом для студентов и школьников, изучающих математику, так как многие калькуляторы показывают детальные шаги расчета, помогая понять, как получен конечный результат.

Объем цилиндрической полости

Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.

На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.

Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.

Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник

Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.

Радиус основания цилиндра, является радиусом цилиндра.

Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.

Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

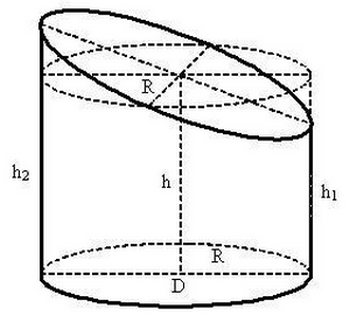
Формула для вычисления объема усеченного цилиндра

Усеченным называется цилиндр, часть которого отрезана плоскостью, пролегающей не параллельно нижней плоскости.

Формула объема усеченного цилиндра следующая:

здесь h₁ b h₂ – наименьшая и наибольшая высоты геометрического тела.

После подстановки значений получится выражение:

Первый: воспользуемся формулой V= \pi r^2 *\frac . Для этого определим радиус нижней плоскости.

r = \frac d= \frac 10=5 см. V=\pi r^2 *\frac = \pi *5^2* \frac = 25 \pi * 20 = 500 \pi \approx 1570,75 см 3 .

Второе решение – подставим диаметр в формулу:

V = \pi \frac * \frac = \pi *\frac * \frac = \pi * \frac * \frac = 500 \pi \approx 1570,75 см 3 .

Зная высоту и радиус или диаметр основания тела, его вместительность высчитывается в несколько действий.

Объем цилиндра по высоте и радиусу

Узнать объем полой фигуры можно моментально, воспользовавшись удобной онлайн-программой. Сервис позволяет за секунды вычислить параметры тела и получить результаты в кубических сантиметрах, метрах, литрах. Расчет производится по двум математическим формулам:

1. По высоте и радиусу: V = S х h.

Где V — объем, S — площадь, h — высота. Чтобы рассчитать объем необходимо площадь основания тела умножить на h. Следовательно, для этого необходимо знать две переменные.

Объём по площади основания и высоте: V = ∏ х R 2 х h

R – радиус, возведенный в квадрат. От первой формулы, расчет отличается тем, что сначала необходимо найти значение радиуса. Для этого диаметр делится на 2 или применяется формула S/2 х ∏ х H. ∏ — константа 3,14 (отношение длины окружности к диаметру).

Задача на нахождение радиуса фигуры

Известно, что общая поверхность круглого прямого цилиндра составляет 60 см2. Чему равен радиус основания цилиндра, если его высота равна 7 см, а фигура имеет лишь одно основание.

Описанный в условии задачи цилиндр представляет собой бочку без крышки, поэтому площадь его поверхности образована не двумя, а одним основанием.

Если учесть названный факт, тогда формула для площади фигуры запишется в следующем виде:

S = pi*r2 + 2*pi*r*h

Подставим все известные из условия величины в это равенство, получим:

60 = 3,14*r2 + 43,96*r =>

3,14*r2 + 43,96*r — 60 = 0

Мы получили классическое полное квадратное уравнение. Его решение даст искомое значение радиуса r. Решаем через дискриминант:

D = 43,962 — 4*3,14*(- 60) ≈ 2686,08;

r = (-43,96±√2686,08)/(2*3,14) = 1,25 см

При решении уравнения отрицательный корень был отброшен, в виду его нефизического значения.

Таким образом, параметры открытого цилиндра из условия задачи составляют 7 см в высоту и 2,5 см в диаметре.

Просмотры: 28

Способ расчета радиуса цилиндра:

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности. Формула радиуса цилиндра: где V – объем цилиндра, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности. Формула радиуса цилиндра: где Sb – площадь боковой поверхности, h – высота

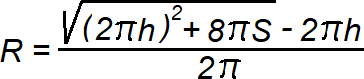
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности. Формула радиуса цилиндра: где S – площадь полной поверхности, h – высота

S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr2=πr (2h+r)

R = √V / πh

где V — объем цилиндра, h — высота.Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:

Формула вычисления объема цилиндра

1. Через площадь основания и высоту

Объем (V) цилиндра равняется произведению его высоты и площади основания.

2. Через радиус основания и высоту

Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:

V = π ⋅ R 2 ⋅ H

Примечание: в расчетах значение числа π округляется до 3,14.

3. Через диаметр основания и высоту

Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:

V = π ⋅ (d/2) 2 ⋅ H

Нет сомнений, что все мы со школьных лет помним, как найти высоту цилиндра, формула выглядит так: H=V/πR^2 или 4V/D^2.

Расшифровать формулу просто:

• V – объем цилиндра;
• π – 3,14;
• R – радиус цилиндра;
• D – диаметр.

То есть получается, что, если разделить объем на площадь основания, получится высота цилиндра.

Можно поступить проще. Для этого нам придется вычислить площадь боковой поверхности искомого цилиндра. Это легко сделать по формуле: S=2πRH. Слегка изменив формулу, получаем: H=S/2πR.

Таким образом, есть уже два способа, которые помогли вспомнить, как найти высоту цилиндра. Это нетрудно, когда перед глазами стройные формулы.

Математические Основы

Цилиндр, как и любая другая геометрическая фигура, имеет свои уникальные формулы для расчета объема

Важно понимать, как эти формулы выводятся и применяются для вычисления объема цилиндра

Формула Объема Цилиндра

Объем (V) цилиндра вычисляется по формуле:

\

где:

• r — радиус основания цилиндра,
• h — высота цилиндра,
• \(\pi\) — математическая константа, приблизительно равная 3.14159.

Принципы Расчета

• Радиус: Чтобы найти объем, необходимо знать радиус основания. Радиус — это расстояние от центра круглого основания до его края.
• Высота: Высота цилиндра измеряется как перпендикулярное расстояние между двумя основаниями.
• Использование \(\pi\): Константа \(\pi\) используется для вычисления площади круга, которая затем умножается на высоту для получения объема.

Примеры Расчета

1. Цилиндр с радиусом 3 м и высотой 5 м:

\

2. Цилиндр с радиусом 2 м и высотой 10 м:

\

Эти примеры иллюстрируют базовый принцип расчета объема цилиндра и демонстрируют, как изменение радиуса и высоты влияет на объем

Важно понимать эти математические принципы для корректного вычисления объемов в различных практических задачах

Похожие калькуляторы

Вам могут пригодиться следующие калькуляторы на эту же тему:

• Калькулятор перевода миллиметров в дюймы. Введите длину в миллиметрах для перевода в дюймы.
• Калькулятор перевода дюймов в миллиметры. Введите длину в дюймах для перевода в миллиметры.
• Калькулятор перевода сантиметров в дюймы. Введите длину в сантиметрах для перевода в дюймы.
• Калькулятор перевода дюймов в сантиметры. Введите длину в дюймах для перевода в сантиметры.
• Калькулятор площади поверхности шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы) с помощью нашего онлайн-калькулятора.
• Калькулятор площади правильного шестиугольника. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью нашего онлайн-калькулятора.
• Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
• Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
• Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
• Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).

Объём цилиндра через площадь основания и высоту

Программа позволяет определить объем тела по обеим формулам. Для этого необходимо только подставить цифры в соответствующие строки и нажать кнопку рассчитать. Пошаговая инструкция вычисления базовых показателей фигуры на калькуляторе по высоте и радиусу:

• в графе «h» ввести длину заданной фигуры, рядом выбрать метрику – в миллиметрах, сантиметрах, метрах;
• в строке «r» ввести радиус тела и выбрать меру длины (мм, см, м);
• в графе «Результат» определить, в чем будет выведен V – кубах, литрах.

Например, длина фигуры составляет 1,6 метра, радиус 25 сантиметров. Объем равен 314.2 литров, 314200 куб. см или 0.314 куб. м. Результат выводится моментально, с точностью до тысячной. Правильность вычисления зависит только от достоверности исходных данных.

Где применяется программа

Сервис разработана для всех пользователей, чья профессиональная деятельность предполагает решение математических задач. Калькулятор будет полезен школьникам 5-9 классов, учащимся 11 классов в подготовительном процессе к ЕГЭ и контрольным срезам, а также родителям для проверки правильности решения задач.

С помощью сервиса можно решить типичные тестовые задания школьной программы, подставляя известные значения и не забывая выставлять метрические параметры (в кубических сантиметрах, кубометрах, миллиметрах, литрах). Например:

1. Дан цилиндр, с площадью основания 58,3 см 2 и высотой 7 см. Чтобы посчитать V следует воспользоваться расчетом через площадь и высоту.

Решение: V = 58,3 см 2 х 7 см = 408.1 см³ или 0.408 л.

Вычисление: перед использованием программы следует определить радиус основания – 16см/2 = 8 см. Затем значения подставить в нужные поля. Расчет производится на основании формулы V = 3,14 х 8 2 х 11 см = 2211.968 см³.

Объем конуса

Рассмотрим конус с высотой h и радиусом основания R. Совместим начало координат с вершиной конуса и направим ось Ох в сторону основания конуса. Тогда она пересечет основание в какой-то точке М c координатой h. Далее через точку М₁ на оси Ох, имеющей координату х, проведем сечение, перпендикулярное оси Ох. Это сечение будет окружностью.

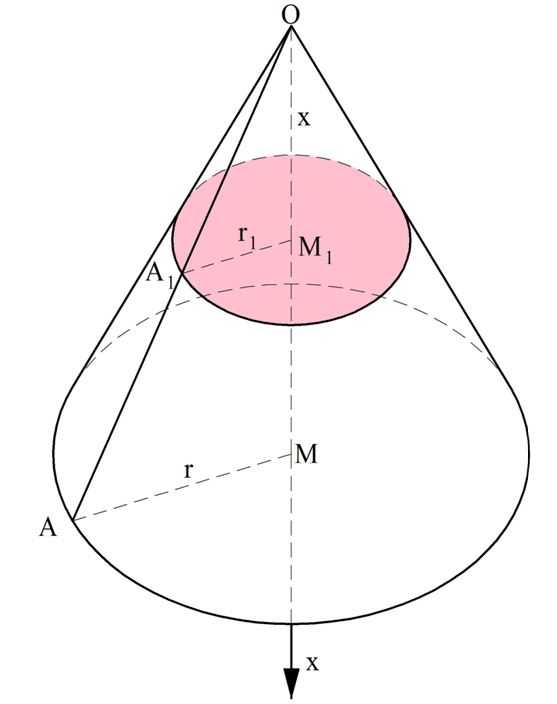
Также построим образующую ОА, которая будет проходить через сечение в точке А₁. Теперь сравним ∆ОАМ и ∆ОА₁М₁. Они прямоугольные, и у них есть общий угол ∠АОМ. Это значит, что они подобны, и поэтому справедливо отношение:

Полученную формулу можно переписать в другом виде так, чтобы она содержала площадь основания, причем она будет похожа на аналогичную формулу для пирамиды:

Задание. Радиус конуса – 8 см, а его высота составляет 12 см. Определите его объем.

Решение. Здесь надо просто применить выведенную формулу:

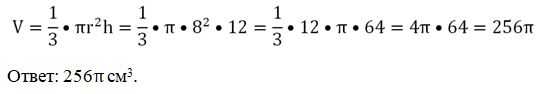
Задание. В сосуде, имеющем форму перевернутого конуса, вода доходит до уровня, соответствующего 2/3 высоты сосуда. При этом ее объем составляет 192 мл. Каков объем всего сосуда?

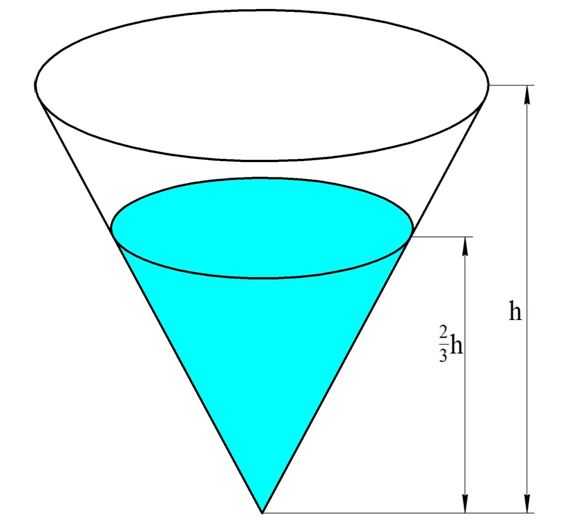
Решение. В задаче фигурируют два конуса. Один из них – это сам сосуд, а второй – его часть, заполненная водой. При выведении формулы объема мы уже выяснили, что радиусы таких конусов пропорциональны их высотам:

Мы уже заметили, что формулы для объема пирамида и конуса идентичны. По сути, конус можно рассматривать как особый случай пирамиды, у которой в основании лежит не многоугольник, а окружность. Аналогично и усеченный конус можно считать особым случаем усеченной пирамиды, а поэтому для расчета его объема можно применять такую же формулу:

Задание. Вычислите объем усеченного конуса с высотой 9 и радиусами оснований 7 и 4.

Решение. Сначала находим площади оснований:

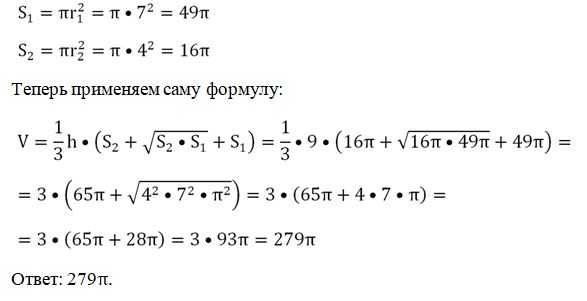
Вычисление объема тел вращения

Телом вращения называют тело, которое может быть получено вращением какой-то плоской фигуры относительно некоторой оси вращения. Например, цилиндр получают вращением прямоугольника вокруг одной из его сторон, а усеченный конус – вращением прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.

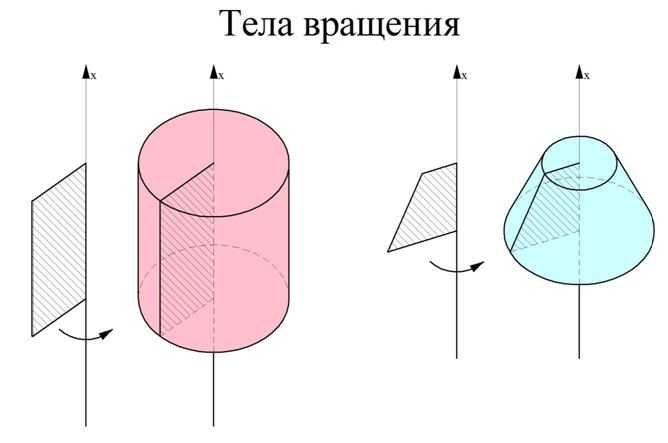
В задачах на вычисление объемов таких тел ось координат Ох уже задана естественным образом – это ось вращения тела. Ясно, что каждое сечение тела, перпендикулярное оси вращения, будет являться кругом.

Рассмотрим случай, когда вокруг оси Ох поворачивают график некоторой функции у = f(x), ограниченный прямыми х = а и у = b. Тогда получится тело, сечениями которого являются круги, причем их радиусы будут равны величине f(x). Напомним, что площадь круга вычисляют по формуле:

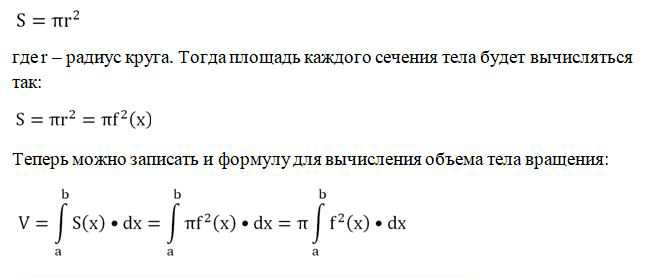
Рассмотрим, как на практике используется эта формула.

Задание. Объемное тело получено вращением ветви параболы

вокруг оси Ох. Оно ограничено плоскостями х = 0 и х = 4. Каков объем такой фигуры?

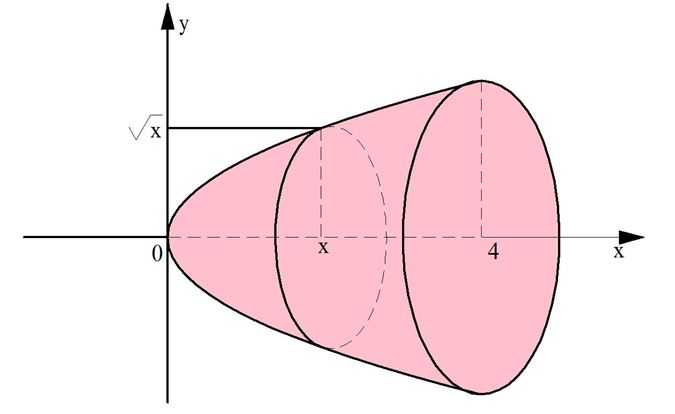
Решение. Здесь пределами интегрирования, то есть числами а и b, будут 0 и 4. Используем формулу для тела вращения:

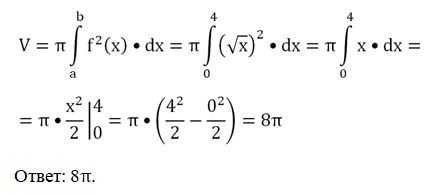
Что такое цилиндр в геометрии

Определения

Цилиндр — это трехмерное геометрическое тело, которое ограничено цилиндрической поверхностью и двумя параллельными плоскостями.

Цилиндрическая поверхность — это поверхность, которая образуется за счет движения в пространстве прямой (образующей) параллельно самой себе, пересекающей данную линию (направляющую).

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Основания — это одинаковые круги, которые ограничивают цилиндр и находятся параллельно друг другу.

Образующая — отрезок, который соединяет точки окружностей оснований цилиндра и перпендикулярный плоскостям этих оснований. Она равна высоте цилиндра или расстоянию от одного его основания до другого.

Объем цилиндрической полости

Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.

На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.

Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.

Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник

Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.

Радиус основания цилиндра, является радиусом цилиндра.

Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.

Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

Заключение

Цилиндр, как геометрическая фигура, играет важную роль в различных областях нашей жизни. Понимание того, как рассчитать его объем, является ключевым навыком во многих профессиональных и академических областях. Этот расчет не только улучшает наше понимание геометрии, но и обеспечивает практическую пользу в инженерии, строительстве, промышленности и многих других сферах. Таким образом, знание и умение применять математические формулы для расчета объема цилиндра открывает двери для решения сложных практических задач и способствует развитию технологических и научных инноваций.

Последние вычисления