Задача огэ по математике про шину 2021 шины

Полезные советы по подготовке

Подготовка к задачам по шинам ОГЭ может быть вызывающей и сложной задачей, но с правильным подходом вы сможете успешно справиться с ней. Вот несколько полезных советов, которые помогут вам в этом процессе:

1. Разберитесь с теорией. Перед тем, как приступить к решению задач, вам нужно хорошо понимать теоретические основы каждого типа задач. Уделите время изучению раздела о шинах в учебнике или других специализированных источниках.
2. Проведите практические тренировки. Решайте множество задач для закрепления полученных знаний. Ищите задачи различной сложности, чтобы укрепить свои навыки и научиться применять изученные концепции в разных ситуациях.
3. Используйте схемы и таблицы. Для упрощения процесса решения задач создавайте схемы и таблицы. Они помогут вам организовать информацию и лучше понять задачу. Также они станут полезным инструментом во время экзамена, когда вы сможете быстро обратиться к ним, чтобы узнать необходимые данные.
4. Прорабатывайте разные типы задач. Шины могут представлять различные типы задач, такие как задачи на расположение объектов на шине, задачи на количественную характеристику распределения объектов и задачи на объем шины. Попробуйте решить каждый тип задачи и изучите его особенности.
5. Сотрудничайте с другими. Попросите своих одноклассников или учителя помочь вам в процессе подготовки и решения задач. Обсуждение задач и способов их решения может помочь вам углубить свое понимание и найти новые подходы к решению.

Следуя этим советам и постоянно тренируясь, вы сможете подготовиться к задачам по шинам ОГЭ и успешно справиться с ними на экзамене. Удачи!

Примеры задач с использованием законов физики и математики

Ниже приведены несколько примеров задач, которые требуют применения законов физики и математики для их решения.

1. Задача о движении тела

Тело начинает движение с постоянным ускорением 3 м/с^2. Найти скорость тела через 5 секунд.

Решение:

1. Используем формулу для скорости в равноускоренном движении: v = u + at, где v — конечная скорость, u — начальная скорость, a — ускорение, t — время.
2. Подставляем известные значения в формулу: v = 0 + 3 * 5 = 15 м/с.

2. Задача о силе тяжести

Найти силу тяжести, действующую на тело массой 10 кг.

Решение:

1. Используем формулу для силы тяжести: F = m * g, где F — сила тяжести, m — масса тела, g — ускорение свободного падения.
2. Подставляем известные значения в формулу: F = 10 * 9.8 = 98 Н.

3. Задача о плотности вещества

Найти плотность вещества, если масса 50 г, а объем 100 см^3.

Решение:

1. Используем формулу для плотности вещества: р = m / V, где р — плотность, m — масса, V — объем.
2. Подставляем известные значения в формулу: р = 50 / 100 = 0.5 г/см^3.

4. Задача о пропорциональности

Сколько стоит 3 кг яблок, если 1 кг стоит 100 рублей?

Решение:

1. Находим соотношение между ценой и массой: p = m * c, где p — цена, m — масса, c — цена за 1 кг.
2. Подставляем известные значения и находим цену: p = 3 * 100 = 300 рублей.

5. Задача о теплопроводности

Какое количество тепла передается через стальную пластину толщиной 5 см, если ее площадь 2 квадратных метра, а теплопроводность 50 Вт/(м·°C)? Разность температур по обоим сторонам пластины равна 20 °C.

Решение:

1. Используем формулу для количества тепла, прошедшего через пластину: Q = (k * A * Δt) / d, где Q — количество тепла, k — коэффициент теплопроводности, A — площадь пластины, Δt — разность температур, d — толщина пластины.
2. Подставляем известные значения в формулу: Q = (50 * 2 * 20) / 0.05 = 40000 Дж.

Решение практико-ориентированных задач ОГЭ 2021г. Задачи про шины

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Решение практикоориентированных задачОГЭ 2021г.Задачи про шиныДля маркировки автомобильных шин применяется единая система обозначений(см. рис. 1). Первое число означает ширину В шины (ширину протектора) вмиллиметрах (см. рис.2). Второе число — высота боковины Н в процентах кширине шины.

English     Русский Правила

Раздел 2: Задачи на анализ данных

Задача 1

Условие:

В таблице указаны данные о количестве пассажиров, проехавших на троллейбусе в разные дни недели в течение месяца:

День недели	Количество пассажиров
Понедельник	25
Вторник	32
Среда	18
Четверг	20
Пятница	40
Суббота	45
Воскресенье	30

Необходимо:

1. Вычислить среднее количество пассажиров, проехавших на троллейбусе в течение месяца.
2. Определить день недели, в который было наибольшее количество пассажиров.
3. Найти день недели с наименьшим количеством пассажиров.

Решение:

1. Чтобы найти среднее количество пассажиров, нужно сложить все числа и разделить их на количество дней:

(25 + 32 + 18 + 20 + 40 + 45 + 30) / 7 = 210 / 7 = 30

Среднее количество пассажиров в течение месяца составляет 30 человек.

2. Чтобы определить день недели с наибольшим количеством пассажиров, нужно найти максимальное значение в столбце «Количество пассажиров» и определить соответствующий день недели:

Наибольшее количество пассажиров — 45, троллейбусом было перевезено в субботу.

3. Чтобы найти день недели с наименьшим количеством пассажиров, нужно найти минимальное значение в столбце «Количество пассажиров» и определить соответствующий день недели:

Наименьшее количество пассажиров — 18, троллейбусом было перевезено в среду.

Задача 2

Условие:

В таблице указаны данные о росте учеников в классе:

Ученик	Рост, см
Иванов	160
Петров	155
Сидоров	162
Козлов	170
Смирнов	150
Новикова	165
Лебедева	168

Необходимо:

1. Вычислить средний рост учеников в классе.
2. Определить ученика с самым большим ростом и его рост.
3. Найти ученика с наименьшим ростом и его рост.

Решение:

1. Чтобы найти средний рост учеников в классе, нужно сложить все значения в столбце «Рост» и разделить их на количество учеников:

(160 + 155 + 162 + 170 + 150 + 165 + 168) / 7 = 1130 / 7 ≈ 161.43

Средний рост учеников в классе составляет приблизительно 161.43 см.

2. Чтобы определить ученика с самым большим ростом и его рост, нужно найти максимальное значение в столбце «Рост» и определить соответствующего ученика:

Ученик Козлов имеет самый большой рост — 170 см.

3. Чтобы найти ученика с наименьшим ростом и его рост, нужно найти минимальное значение в столбце «Рост» и определить соответствующего ученика:

Ученик Смирнов имеет наименьший рост — 150 см.

ОГЭ 2020 Математика. Разбор заданий 1-5 «Маркировка автомобильных шин”

Для маркировки автомобильных шин применяется единая система обозначений (см. таблицу).

Первое число означает ширину В шины (ширину протектора) в миллиметрах (см. рисунок).

Второе число — отношение высоты боковины Н к ширине шины В в процентах.

Последующая буква указывает конструкцию шины.

1. Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 16 дюймам? Ответ дайте в миллиметрах.

1. Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 16 дюймам? Ответ дайте в миллиметрах.

Воспользуемся таблицей разрешенных размеров шин. Для 16 дюймов подходят 185/50, 195/45, 205/45. Нам нужна наименьшая ширина, это 185.

2. На сколько миллиметров радиус колеса с маркировкой 195/60 R14 больше, чем радиус колеса с маркировкой 165/70 R14?

Ширина первой шины равна 195 мм, а отношение высоты боковины к ширине равно H/B = 60% = 0,6.

Найдем эту самую высоту боковины: Н = 0,6В = 0,6 · 195 = 117мм.

Далее нам известен диаметр внутреннего отверстия шины: d = 14 дюймов. Переведём их в миллиметры. По условию задачи 1 дюйм равен 25,4 мм. 14 · 25,4 = 355,6 мм.

D = 2Н + d = 2 · 117 + 355,6 = 589,6мм;

То же самое проделываем со второй шиной и находим R2.

Ширина шины B равна 165; Н/В = 70% = 0,7.

d = 14 дюймов = 14 · 25,4 = 355,6 мм.

D = 2Н + d = 2 · 115,5 + 355,6 = 586,6мм;

И, наконец, найдем разницу между радиусами этих двух шин:

3.Найдите диаметр D колеса автомобиля, выходящего с завода. Ответ дайте в сантиметрах.

Очень внимательно читаем задание. По условию задачи завод производит колеса с маркировкой 175/60 R15, хотя на рисунке указаны совсем другие значения. Будьте внимательнее, некоторые рисунки даны для лучшего представления задачи.

Как найти D мы уже знаем из предыдущей задачи.

Из маркировки становится понятно, что ширина шины В равна 175 мм, отношение Н к В равно 60% = 0,6, откуда Н = 0,6 · 175 = 105, и диаметр d равен 15 дюймам или 15 · 25,4 = 381 мм.

D = 2Н + d = 2 · 105 + 381 = 591 мм.

Но ответ нам надо дать в сантиметрах, поэтому результат делим на 10.

4. На сколько миллиметров уменьшится диаметр D колеса, если заменить шины, установленные на заводе, шинами с маркировкой 195/45 R16?

Диаметр D исходной заводской шины мы уже находили, он равен 591 мм. Найдем диаметр D шины с маркировкой 195/45 R16 (аналогично предыдущим задачам).

Высота боковины Н = 0,45 · 195 = 87,75.

Диаметр внутреннего отверстия d = 16 дюймов = 16 · 25,4 = 406,4 мм.

D = 2Н + d = 2 · 87,75 + 406,4 = 581,9 мм.

Посчитаем на сколько уменьшится диаметр, если шины заменить.

5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить шины, установленные на заводе, шинами с маркировкой 195/55 R15? Округлите результат до десятых.

При одном обороте колеса шина проходит расстояние, равное длине его окружности. Чтобы найти длину окружности надо воспользоваться формулой L = 2πR (формула есть в справочном материале)

Так как 2R=D, то формулу можно преобразовать L = πD.

Диаметр D исходной заводской шины мы уже находили, он равен 591 мм.

Найдем диаметр D шины с маркировкой 195/55 R15

D = 2 · 0,55 · 195 + 15 · 25,4 = 214,5 + 381 = 595,5мм.

Найдем длины окружностей шин.

Перемножу сразу крест накрест, чтобы дроби не писать. Что же получится?

Обе части уравнения можно разделить на π

Если изначально пробег был 100%, то получается что увеличение составило 100,76%-100%=0,76%. Округлим до десятых.

Источник

Решение Ященко ОГЭ 2023 Вариант №4 (10 вариантов) Математика

Решение заданий варианта №4 из сборника ОГЭ 2023 по математике И.В. Ященко 10 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.

ЧАСТЬ 1

Задание 1-5.Автомобильное колесо, как правило, представляет из себя металлический диск, с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.

Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65R15 (см. рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр В на рисунке 2). Второе число (число 65 в приведённом примере) – процентное отношение высоты боковины (параметр Н на рисунке 9) к ширине шины, то есть 100\cdot \frac{H}{B}.

Задание 6.Найдите значение выражения \frac{5}{12}+\frac{7}{12}\cdot 1\frac{3}{7}.

Задание 7.На координатной прямой точки A, B, C и D соответствуют числам –0,74; –0,047; 0,07; –0,407.

Какой точке соответствует число –0,047? 1) А 2) В 3) С 4) D

Задание 8. {4}}} при а = 7 и b = 9.

Задание 9.Найдите корень уравнения x+\frac{x}{9}=-\frac{10}{3}.

Задание 10.В сборнике билетов по математике всего 40 билетов, в 18 из них встречается вопрос по теме «Неравенства». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос по теме «Неравенства».

Задание 11.На рисунках изображены графики функций вида у = kх + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.КОЭФФИЦИЕНТЫ

1) k < 0, b < 02) k < 0, b > 03) k > 0, b > 0

ГРАФИКИ

В таблице под каждой буквой укажите соответствующий номер.

Задание 12.В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C = 8500 + 6800n, где n – число колец, установленных в колодце.

Задание 13.Укажите решение системы неравенств \begin{cases} x+3,2\le 0, \\ x+1\le -1. \end{cases}

Задание 14.На клетчатой бумаге с размером клетки 1×1 нарисована «змейка», представляющая из себя ломаную, состоящую из чётного числа звеньев, идущих по линиям сетки. На рисунке изображён случай, когда последнее звено имеет длину 10. Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину 190.

Задание 15.На стороне АС треугольника ABC отмечена точка D так, что AD = 6, DC = 8. Площадь треугольника ABC равна 42. Найдите площадь треугольника ABD.

Задание 16.Угол А четырёхугольника ABCD, вписанного в окружность, равен 37°. Найдите угол С этого четырёхугольника.

mm

Задание 23.Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 16, а одна из диагоналей ромба равна 64. Найдите углы ромба.

Задание 24.Внутри параллелограмма ABCD выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади параллелограмма.

Задание 25.В трапеции ABCD боковая сторона АВ перпендикулярна основанию ВС. Окружность проходит через точки С и D и касается прямой АВ в точке Е. Найдите расстояние от точки Е до прямой CD, если AD = 8, ВС = 7.

Источник варианта: Сборник ОГЭ 2023 по математике. Типовые экзаменационные варианты. 10 вариантов. Под редакцией И.В. Ященко.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 0 / 5.

Как выбрать правильный диаметр для своего автомобиля

Правильный диаметр автомобильной резины играет важную роль в безопасности и комфорте вождения. Неправильный диаметр может повлиять на управляемость автомобиля и привести к поломке шины или подвески.

Определение правильного диаметра шины осуществляется на основе трех параметров:

1. Ширина профиля: ширина резины измеряется в миллиметрах и указывается на боковой стенке шины. Чтобы выбрать правильную ширину профиля, необходимо учитывать рекомендации производителя автомобиля и общие параметры автомобиля.
2. Высота профиля: высота профиля также измеряется в миллиметрах и указывается на боковой стенке шины. Высота профиля влияет на амортизацию и комфортность езды. Как правило, более высокий профиль обеспечивает лучшую амортизацию, но менее точное управление.
3. Диаметр диска: диаметр диска измеряется в дюймах и указывается на боковой стенке диска. Для выбора правильного диаметра диска необходимо учитывать не только размеры текущей резины, но и рекомендации производителя автомобиля.

При выборе новой резины важно соблюдать все указанные параметры. Неправильный диаметр может повлиять на показатели общей динамики автомобиля, подвески и безопасности

Если вы не уверены, какой диаметр выбрать, лучше проконсультироваться с автомехаником или обратиться к рекомендациям производителя автомобиля. Они помогут вам выбрать правильный диаметр для вашего автомобиля и обеспечить безопасность и комфортность вождения.

Маркировка шин в ОГЭ 1-5 задания.

Маркировка шин в ОГЭ 1-5 задания.

Просмотр содержимого документа «Маркировка шин в ОГЭ 1-5 задания.»

Маркировка шин в ОГЭ 1-5 задания.

Приветствую вас школьники на своем канале. В этом выпуске разберем задание на «Маркировку шин» 1-5 задание.

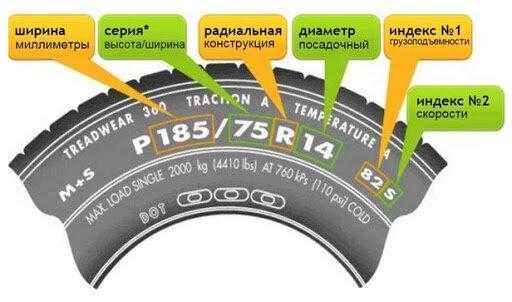
В этом тексте задачи, необходимо обратить внимание на следующие данные:

1) Первое число в маркировки — это ширина шины, которая нужна при ответе на первый вопрос.

2) Второе число — это число взятое в процентах от первого числа, т.е. второе число делите на 100 и умножаете на первое число.

4) По рисунку 2 нужно составить формулу для вычисления диаметра колеса, который понадобится для задания со 2 по 5 включительно.

Задания на шины легкие, расчеты все делаются по одной формуле, только нужна внимательность при вычислениях.

После основного текста задачи, идет следующий текст и таблица:

Из текста жирным шрифтом, нам нужна будет заводская маркировка шины. В нашем случае это 185/70 R14.

Таблица приведена для первого вопроса.

Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 16 дюймов?

Ответ на этот вопрос приведен в картинке ниже.

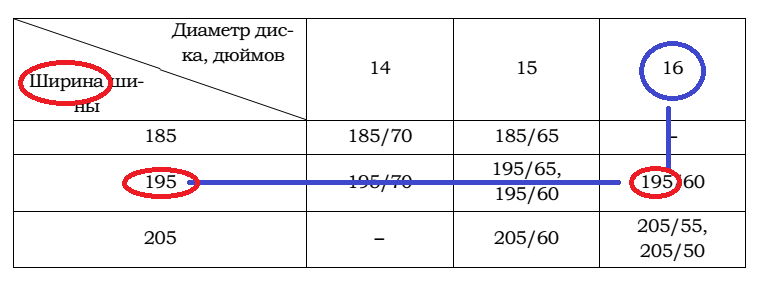
Ответ на первый вопрос: 195

Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.

Заводская маркировка шины в нашем случае это 185/70 R14.

По рисунку 2, составим формулу для нахождения диаметра колеса.

а) Найдем значение высоту боковины шины — Н. Это второе число в маркировке выраженное в % от 185. Т.е. нужно найти 70% от 185.

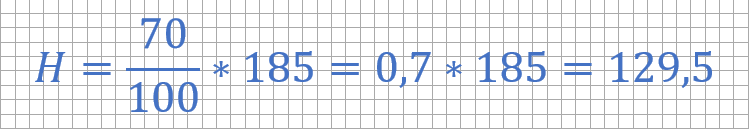
б) Найдем диаметр диска колеса. В маркировке это число 14, выраженное в дюймах. Нам нужно это число перевести в мм.

Подставим все значения в нашу формулу, и найдем диаметр колеса.

На сколько миллиметров увеличится диаметр колеса, если заменить шины, установленные на заводе на шины 195/70 R14?

Для ответа на этот вопрос, диаметр колеса установленного на заводе, нашли во втором задании, оно равно 614,6

Найдем диаметр колеса с маркировкой 195/70 R14 Обратите внимание, что это маркировка отличается от заводской, только первым числом, шириной шины. Все вычисления одинаковые

Все вычисления одинаковые.

Теперь ответим на вопрос, найдем на сколько увеличился диаметр колеса

На сколько метров увеличится путь, пройденный автомобилем, когда колесо сделает 1000 оборотов, если заменить шины установленные на заводе шинами с маркировкой 195/70 R14? Округлите результат до целых.

Ответить на вопрос можно очень быстро, если правильно разобраться с текстом вопроса.

Что означает один оборото колеса? Если у автомобиля колесо сделает один оборот, то машина проедет расстояние равное длине окружности.

Как связан между собой диаметр колеса (D) и длина окружности (С)?

Из формулы видно, что путь пройденный автомобилем зависит от его диаметра колеса.

Но тогда зачем в задании дано 1000 оборотов? Показываю два варианта решение, а там выбирайте, что легче.

Найдем сколько метров проедет колесо за 1000 оборотов, выпушенное с завода:

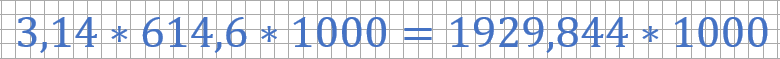
Заводское колесо при умножении на 1000 оборотов, проедет 1929844 мм. В задании нужно ответ дать в метрах, значит нужно будет поделить на 1000, и получится 1929,844 метра.

б) Найдем сколько метров проедет колесо за 1000 оборотов с маркировкой 195/70 R14.

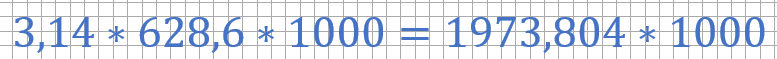
Здесь не стали умножать на 1000, поскольку 1973,804 это и есть метры, как и в заводском колесе.

Ответим на вопрос задания: На сколько метров увеличится путь?

Так как диаметр колеса связан с длиной окружности следующей формулой:

Значит для того, чтобы узнать на сколько метров увеличится путь, можно выполнить следующее:

Как видите, достаточно умножить число «пи» на разницу между диаметрами колес.

Спидометр автомобиля, собранного на заводе, показывает скорость точно. На сколько процентов показания спидометра будут меньше скорости автомобиля, если заменить шины, установленные на заводе шинами с маркировкой 195/70 R14? Округлите результат до десятых.

В этом вопросе, нам нужны только диаметры колес, поскольку показание спидометра зависит от диаметра колеса.

Спидометр, при диаметре колеса, которое поставили на заводе (D=614,6) показывает точно, значит это значение возьмем за 100%

Диаметр колеса с маркировкой 195/70 R14 возьмем за Х.

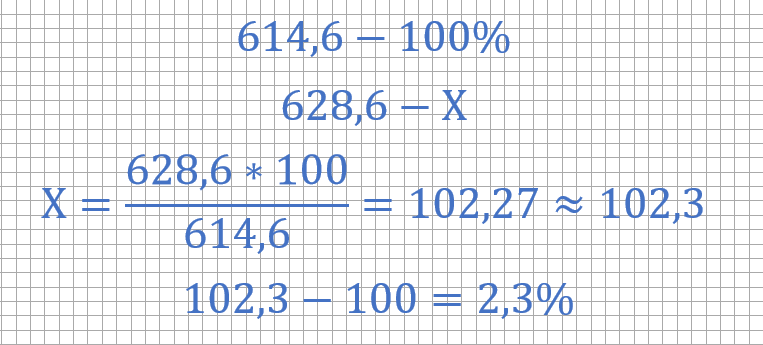
Как видите, нужно поделить диаметры колес и умножить на 100%.

И не забывайте потом из результата вычесть 100%.

• Свежие записи
  • Нужно ли менять пружины при замене амортизаторов
  • Скрипят амортизаторы на машине что делать
  • Из чего состоит стойка амортизатора передняя
  • Чем стянуть пружину амортизатора без стяжек
  • Для чего нужны амортизаторы в автомобиле

презентация по подготовке к ОГЭ | Презентация к уроку по алгебре (9 класс):

Слайд 1

Решение практико-ориентированных задач Задачи про шины

Слайд 2

Для маркировки автомобильных шин применяется единая система обозначений (см. рис. 1 ). Первое число означает ширину В шины (ширину протектора ) в миллиметрах (см. рис.2). Второе число — высота боковины Н в процентах к ширине шины . Последующая буква означает конструкцию шины. Например, буква R значит, что шина радиальная , то есть нити каркаса в боковине шины расположены Вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса в дюймах ( в одном дюйме 25,4 мм ). По сути, это диаметр d внутреннего отверстия в шине. Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Последний символ в маркировке — индекс скорости .

Слайд 3

Диаметр диска (дюймы) Ширина шины(мм) 17 18 19 20 215 215/65 215/60 Не разр . Не разр . 225 225/60 225/55, 225/60 225/50 Не разр . 235 Не разр . 235/55 235/50 235/45 3

Слайд 4

1. Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 19 дюймам ? Ответ дайте в миллиметрах. Диаметр диска (дюймы) Ширина шины(мм) 17 18 19 20 215 215/65 215/60 Не разр . Не разр . 225 225/60 225/55, 225/60 225/50 Не разр . 235 Не разр . 235/55 235/50 235/45 Ответ : 225 4

Слайд 5

2. На сколько миллиметров радиус колеса с маркировкой 215/60 R18 меньше , чем радиус колеса с маркировкой 235/55 R18 ? 1) 215/60 R18 D=d+2H H=215*0,6=129 d=25,4*18=457,2 мм D=457,2+2*129=715,2 мм R=D :2=715,2:2=357,6мм 2) 235/55 R18 D=d+2H H=235*0,55=129,25 d=25,4*18=457,2 мм D=457,2+2*129,25=715,7 мм R=D :2=715,7:2=357,85мм 357,85-357,6=0,25 мм

Слайд 6

3.

Слайд 7

4. На сколько миллиметров уменьшится диаметр D колеса, если заменить шины, установленные на заводе, шинами с маркировкой 235/45 R20? Решение. Диаметр колеса автомобиля, выходящего с завода D1= 727,2 мм Диаметр колеса с шинами с маркировкой 235/45 R20 D 2 = d + 2H= 20∙ 25,4 + 2∙ 0,45∙ 235 = 508 + 211,5 = 719,5мм D 1 – D 2 = 727,2 – 719,5 = 7,7 мм Ответ : 7, 7

Слайд 8

5. На сколько процентов уменьшится пробег автомобиля при одном обороте колеса , если заменить шины, установленные на заводе, шинами с маркировкой 235/45 R20 ? Округлите результат до десятых. Решение. Диаметр колеса автомобиля, выходящего с завода D1= 727,2 мм, 1 оборот = С = П D 1 = 727,2 П мм Диаметр колеса с шинами с маркировкой 235/45 R20 D 2 = 719,5мм, радиус 1 оборот = С = П D 2 = 7 19 , 5 П мм Пусть 727,2 П – 100% 7 19 , 5 П – х% х% = 7 19 , 5 П ∙ 100% : 727,2 П ≈ 98,9% 100% — 98,9% = 1,1% Ответ : 1,1 8

Слайд 9

Попробуйте решить самостоятельно

Раздел 3: Задачи на применение знаний о материалах

Задача 1

В таблице приведены свойства трех материалов: алюминия, стали и пластика. Используя эти данные, ответьте на следующие вопросы:

Материал	Плотность, г/см³	Теплопроводность, Вт/(м·К)	Теплоемкость, Дж/(г·К)
Алюминий	2.7	205	0.9
Сталь	7.8	50	0.46
Пластик	1.2	0.19	1.9

1. Какой материал имеет наибольшую плотность?
2. Какой материал обладает наибольшей теплопроводностью?
3. Какой материал обладает наибольшей теплоемкостью?

Задача 2

Изучая свойства различных материалов, ученик сделал следующие выводы:

1. Материал с высокой плотностью имеет малую теплопроводность.
2. Материал с большой теплопроводностью имеет невысокую теплоемкость.
3. Материал с невысокой теплоемкостью обладает малой плотностью.

Определите, какие из этих выводов являются верными, и объясните свой ответ.

Задача 3

Изготавливая предметы из металлического сплава, необходимо знать его температурный коэффициент линейного расширения. В таблице приведены данные для нескольких сплавов:

Сплав	Температурный коэффициент линейного расширения, 1/°C
Сплав А	12 × 10-6
Сплав Б	15 × 10-6
Сплав В	9 × 10-6

Укажите сплавы, которые будут лучше всего подходить для изготовления предметов, которые будут использоваться при значительных изменениях температуры (например, в авиации).

Подробное объяснение основных понятий

Для успешного решения задач по шинам в ОГЭ необходимо освоить основные понятия, используемые в заданиях. Рассмотрим их подробнее:

Массив

Массив — это упорядоченная совокупность элементов одного типа, расположенных в памяти компьютера. Каждый элемент массива имеет уникальный индекс, который позволяет обращаться к нему по отдельности. Например, массив целых чисел имеет пять элементов, а индексы элементов массива начинаются с 0 и заканчиваются на 4.

Индекс

Индекс — это числовое значение, используемое для обращения к элементу массива. Индексы в массивах начинаются с 0. Например, для массива индексы элементов будут следующими: 0 — для числа 1, 1 — для числа 2, 2 — для числа 3 и так далее.

Оператор присваивания

Оператор присваивания — это оператор, который используется для присваивания значения одной переменной или выражения другой переменной. Обычно выглядит так: =. Например, в выражении x = 5; значение 5 присваивается переменной x.

Декремент

Декремент — это операция уменьшения значения переменной на 1. Обозначается символом —. Например, x—; уменьшит значение переменной x на 1.

Условный оператор

Условный оператор — это оператор, который позволяет выполнять определенный блок кода только при выполнении определенного условия. В языке программирования JavaScript условный оператор выглядит следующим образом: if (условие) { выполняемый блок кода }. Например, если x больше 0, то выполнится блок кода внутри фигурных скобок.

Цикл

Цикл — это управляющая структура, которая позволяет выполнять определенный блок кода несколько раз. В языке программирования JavaScript применяются различные типы циклов, такие как цикл for, цикл while и цикл do while.

Функция

Функция — это набор инструкций, который выполняет определенную задачу и может быть вызван при необходимости. Функция может иметь параметры (входные данные) и возвращать результат. В языке программирования JavaScript функции объявляются с помощью ключевого слова function. Например, функция для вычисления суммы двух чисел может выглядеть следующим образом: function sum(a, b) { return a + b; }.

Операция деления по модулю

Операция деления по модулю — это операция, которая возвращает остаток от деления одного числа на другое. В языке программирования JavaScript операция деления по модулю обозначается символом %. Например, результат операции 7 % 3; будет равен 1, так как при делении 7 на 3 остатком будет 1.

Условный оператор switch

Условный оператор switch используется для выполнения различных действий в зависимости от значения переменной или выражения. Он действует по принципу переключателя и позволяет проверить различные варианты значений. В языке программирования JavaScript оператор switch выглядит следующим образом:

switch (выражение) {	// код, который будет выполняться при совпадении значения выражения со значением case	case значение1:	код;	break;	case значение2:	код;	break;	default:	код;	break;	}
Выражение сравнивается с каждым значением case, и если значение совпадает, выполняется соответствующий код. Если совпадение не найдено, выполняется код в блоке default.

Почему важно знать задачи про шины ОГЭ 2023

Задачи про шины являются одним из ключевых элементов заданий по ОГЭ 2023 года. Они проверяют не только знания и навыки учащихся в области математики, но и развивают логическое мышление, аналитические способности и умение применять полученные знания на практике.

Знание задач про шины ОГЭ 2023 позволит учащимся быть готовыми к решению заданий финального экзамена. Они помогут понять основные принципы, которые лежат в основе данных задач, а также научат структурировать информацию и работать с большими объемами данных.

Опыт решения задач про шины также поможет учащимся научиться находить решения в нестандартных ситуациях, что в дальнейшем пригодится им как в учебе, так и в реальной жизни. Они могут столкнуться с задачами, где требуется анализировать сложные ситуации, применять математические модели и строить графики или таблицы для удобства решения.

Примеры задач про шины ОГЭ 2023

1. В автомобильном магазине есть шины разных компаний: A, B, C, D. Цены на шины следующие:

• Шины A стоят 3000 рублей за штуку.
• Шины B стоят 3200 рублей за штуку.
• Шины C стоят 3500 рублей за штуку.
• Шины D стоят 4000 рублей за штуку.

Какую самую дешевую комбинацию шин можно купить для автомобиля, состоящего из четырех шин?

Ответ: Самая дешевая комбинация шин будет состоять из шин A, так как они стоят 3000 рублей за штуку. Следовательно, самая дешевая комбинация будет стоить 4 * 3000 = 12000 рублей.

2. В автосервисе имеется 10 шин разных марок. Известно, что 7 из них соответствуют нормам качества и могут быть использованы при дальнейшем обслуживании автомобилей. Какова вероятность, что при случайном выборе двух шин хотя бы одна окажется качественной?

Ответ: Чтобы рассчитать вероятность выбора как минимум одной качественной шины, необходимо вычислить вероятность выбора двух не качественных шин и отнять ее от 1. Вероятность выбора двух не качественных шин равна (3/10) * (2/9) = 6/90. Следовательно, вероятность выбора хотя бы одной качественной шины равна 1 — 6/90 = 84/90 = 14/15.

Это лишь два примера задач про шины ОГЭ 2023, которые могут встретиться на экзамене. Решение подобных задач поможет учащимся развить уверенность в себе, приобрести привычку к анализу информации и применению математических методов в решении практических задач.

Примеры задач с шинами с разбором и объяснением решения

1. Задача: Вагончик отходит от станции с равномерной скоростью 60 км/ч в сторону противоположного пути. Через 10 минут после отхода вагончика от станции с этой же станции в сторону вагона отправляется велосипедист с постоянной скоростью 20 км/ч. Через какое время велосипедист догонит вагончик?

Решение: Чтобы решить эту задачу, нужно выразить расстояние, которое проходит вагончик, как функцию от времени, а затем приравнять его расстоянию, которое прошел велосипедист. Величина расстояния равна произведению скорости на время.

Пусть время вагончика будет x, тогда расстояние, которое он прошел, будет равно 60x.

Велосипедист движется на 10 минут медленнее, поэтому его время будет x — 10/60 (переводим велосипедиста в часы). Расстояние, которое прошел велосипедист, будет равно 20(x — 1/6).

Итак, уравнение будет выглядеть так: 60x = 20(x — 1/6).

Решая это уравнение, мы найдем, что x = 1/2.

Ответ: Велосипедист догонит вагончик через 30 минут после его отхода от станции.

2. Задача: Два шиномонтажных цеха работают с разной скоростью. Первый цех меняет все шины на машине за 4 часа, а второй цех меняет все шины за 3 часа. Сколько времени потребуется обоим цехам вместе, чтобы поменять шины на двух машинах?

Решение: Чтобы решить эту задачу, нужно выразить работу каждого цеха в терминах времени. Работа равна произведению скорости на время.

Первый цех меняет все шины за 4 часа, поэтому его скорость будут равна 1/4 шины в час.

Второй цех меняет все шины за 3 часа, поэтому его скорость будет равна 1/3 шины в час.

Оба цеха работают одновременно на двух машинах. Общая скорость работы будет сложением скоростей каждого цеха. То есть, скорость общей работы будет равна (1/4 + 1/3) шины в час.

Чтобы узнать, сколько времени потребуется обоим цехам вместе, чтобы поменять шины на двух машинах, нужно разделить работу на общую скорость работы.

Работа про две машины будет равна 2 шины.

Общая скорость работы будет равна (1/4 + 1/3) шины в час.

Итак, всего времени потребуется равно 2 / (1/4 + 1/3) = 24/7 часов.

Ответ: Обоим цехам потребуется около 3 часов и 26 минут, чтобы поменять шины на двух машинах.

3. Задача: Велосипедист и мотоциклист отправились из одного города в другой, примерно находящихся на расстоянии 75 км друг от друга. Если велосипедист движется со скоростью 15 км/ч, а мотоциклист — со скоростью 30 км/ч, через какое время они встретятся?

Решение: Чтобы решить эту задачу, нужно выразить расстояние, которое проходит каждый из них, как функцию от времени, и приравнять эти расстояния.

Пусть время, в которое встретятся велосипедист и мотоциклист, будет t.

Велосипедист проходит 15t км.

Мотоциклист проходит 30t км.

Расстояние между городами составляет 75 км.

Итак, уравнение будет выглядеть так: 15t + 30t = 75.

Решая это уравнение, мы найдем, что t = 2.

Ответ: Велосипедист и мотоциклист встретятся через 2 часа.