Цилиндр. виды, объём цилиндра, площадь поверхности

Ответ нейросети Pifagor.AI

Для решения данной задачи воспользуемся теоремой Гаусса. Согласно теореме Гаусса, поток вектора напряженности электрического поля через закрытую поверхность равен алгебраической сумме зарядов, содержащихся внутри этой поверхности, деленной на диэлектрическую проницаемость среды.

Для начала найдем алгебраическую сумму зарядов, содержащихся внутри закрытой поверхности. В данной задаче имеем два коаксиальных цилиндра с поверхностными плотностями заряда σ1 и σ2. Поскольку заряд равномерно распределен по поверхности цилиндров, сумма зарядов равна произведению плотности заряда на площадь поверхности цилиндра.

Площадь поверхности цилиндра можно найти по формуле \(S=2\pi RL\), где R — радиус цилиндра, L — длина цилиндра. В нашем случае L не задано, поэтому предположим, что длина цилиндров достаточно большая, чтобы поверхностная плотность заряда была равномерной по всей поверхности.

Таким образом, сумма зарядов внутри поверхности равна \(Q_1 = \sigma_1 S_1\) и \(Q_2 = \sigma_2 S_2\).

Подставим известные значения и вычислим сумму зарядов:
\(Q_1 = \sigma_1 \cdot 2\pi R_1 L\) и \(Q_2 = \sigma_2 \cdot 2\pi R_2 L\).

Теперь, применив теорему Гаусса, можно найти напряженность электрического поля в зависимости от расстояния до оси цилиндров.

Так как цилиндрическая симметрия, и поле направлено радиально от центра, воспользуемся гауссовой поверхностью в виде цилиндра радиусом r и высотой h. Интеграл по поверхности можно свести к интегралу по боковой поверхности и основаниям.

Интеграл по боковой поверхности равен \(\int E \cdot ds\), где ds — элемент длины поверхности, равный 2πrh, r — расстояние от оси цилиндров до гауссовой поверхности.

Интеграл по основаниям равен \(E \cdot 2\pi rL\), так как поверхностная плотность заряда равномерна по всей поверхности и поле параллельно оси.

Из теоремы Гаусса следует, что поток вектора напряженности электрического поля через закрытую поверхность равен зарядам, содержащимся внутри этой поверхности, деленному на диэлектрическую проницаемость среды, т.е.
\(\Phi = \frac{{Q_1 + Q_2}}{{\varepsilon_0}} = E \cdot (2\pi rL + 2\pi rL) = E \cdot 4\pi rL\).

Также, заряды внутри поверхности равны \(Q_1 = \sigma_1 \cdot 2\pi R_1 L\) и \(Q_2 = \sigma_2 \cdot 2\pi R_2 L\), поэтому
\(E \cdot 4\pi rL = \frac{{\sigma_1 \cdot 2\pi R_1 L + \sigma_2 \cdot 2\pi R_2 L}}{{\varepsilon_0}}\).

Упростим выражение, деля все на \(2\pi L\):
\(E \cdot 2r = \frac{{\sigma_1 \cdot R_1 + \sigma_2 \cdot R_2}}{{\varepsilon_0}}\).

Теперь подставим значения \(\sigma_1 = 4\sigma\) и \(\sigma_2 = -\sigma\), а также значения радиусов и плотности заряда:
\(E \cdot 2r = \frac{{4\sigma \cdot R_1 — \sigma \cdot R_2}}{{\varepsilon_0}} = \frac{{4 \cdot 50 \cdot 10^{-9} \cdot 10^{-1} — 50 \cdot 10^{-9} \cdot 4 \cdot 10^{-1}}}{{8.854 \cdot 10^{-12}}}\).

Остается найти напряженность электрического поля E(r), деля полученное выражение на 2r:

\(E(r) = \frac{{4 \cdot 50 \cdot 10^{-9} \cdot 10^{-1} — 50 \cdot 10^{-9} \cdot 4 \cdot 10^{-1}}}{{8.854 \cdot 10^{-12} \cdot 2 \cdot 10^{-1}}}\).

Теперь можно подставить числовые значения и вычислить \(E(r)\):

\[
E(r) \approx 677.77 \cdot 10^{-8} \, \text{Н/Кл}
\]

График зависимости напряженности электрического поля E(r) будет иметь вид прямой линии, так как E(r) не зависит от r. То есть, E(r) будет постоянной величиной и равной \(677.77 \cdot 10^{-8}\, \text{Н/Кл}\).

Ответ помог?

II.2.2. Расчет угловых коэффициентов

Угловой коэффициент является основной расчетной величиной. Он может быть найден аналитическим, графоаналитическим методами. Методом поточной алгебры и численно при помощи ЭВМ. Первые три метода изложены в . Рассмотрим подробно аналитический метод определения угловых коэффициентов.

Аналитический метод основан на непосредственном интегрировании математического выражения для элементарного углового коэффициента. Рассмотрим в качестве примера систему, приведенную на рис. 2.1, если тела имеют диффузное отражение.

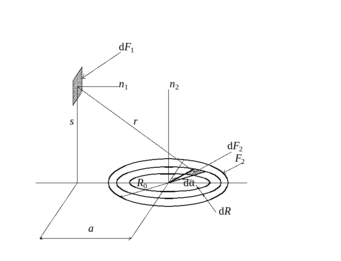
Рис. 2.1. Элемент плоскости и перпендикулярный ему круглый диск

Найдем значения величин, входящих в зависимость . Эти величины, входящие в это выражение, определяются следующим образом:

При

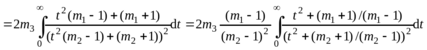
Далее обозначим первый интеграл последнего выражения через I₁, а второй через I₂. Для вычисления интеграла I₂ воспользуемся рекуррентной формулой . Получим

С учетом полученных соотношений продолжим вычисления:

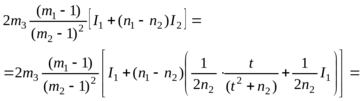
После преобразования будем иметь

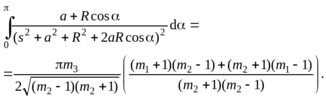
Обозначив через V₁ и V₂ соответственные члены последнего выражения , проведем вычисления далее:

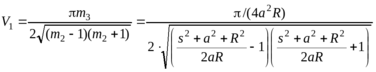
Теперь вычислим второй интеграл:

Подставив в это выражение

Обозначив интегралы последнего выражения соответственно через A₁ и A₂, преобразуем их (первый при

Пусть

Так как при интегрировании по  мы взяли интеграл на участке от 0 до , а реально необходимо интегрировать от 0 до 2, то полученное выражение необходимо умножить на 2.

Теперь рассмотрим пример расчета углового коэффициента для системы, состоящей из двух соосных круглых дисков (рис. 2.2).

Рис. 2.2. Два параллельных соосных диска

Определим все величины, входящие в зависимость

Первоначально вычислим

RF₁rsaRaR₁₂srF₂RRd

Рис. II.3. Круглый диск и параллельный ему элемент плоскости

Этот интеграл вычисляется аналогично интегралу (2.6).

Далее вычислим

aR₁RR₂₀

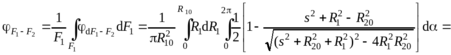
При последнее выражение будет иметь вид

В итоге получим, что для двух соосных параллельных дисков радиусами R₁ и R₂ угловой коэффициент

Далее в табл. 2.1 приведем формулы для определения угловых коэффициентов для наиболее часто встречающихся комбинаций поверхностей.

Таблица 2.1. Расчетные формулы угловых коэффициентов.

Геометрическое положение плоскостей (фигура)

Комбинация поверхностей; расчетная формула

Два бесконечно малых произвольно ориентированных элемента;

Две бесконечные пластины, имеющие одну общую сторону;

Две бесконечные пластины, параллельные друг другу;

Два бесконечно длинных параллельных цилиндра с одинаковым радиусом;

Внутренняя поверхность и торцы усеченного конуса;

Два параллельных соосных диска;

Полоса и цилиндр бесконечной длины;

1.5. Объем цилиндра

Если геометрическое тело простое, то есть допускает разбиение на конечное число треугольных пирамид, то его объем равен сумме объемов этих пирамид. Для произвольного тела объем определяется следующим образом.

Данное тело имеет объем V, если существует содержащие его простые тела и содержащиеся в нем простые тела с объемами, сколько угодно мало отличающимися от V.

Применим это определение к нахождению объема цилиндра с радиусом основания R и высотой Н.

При выводе формулы для площади круга были построены такие два n-угольника (один − содержащий круг, другой − содержащийся в круге), что их площади при неограниченном увеличении n неограниченно приближались к площади круга. Построим такие многоугольники для круга в основании цилиндра. Пусть Р − многоугольник, содержащий круг, а Р’ − многоугольник, содержащийся в круге (рис. 6).

Рис. 7 − Цилиндр с описанной и вписанной в него призмой

Построим две прямые призмы с основаниями Р и Р’ и высотой Н, равной высоте цилиндра. Первая призма содержит цилиндр, а вторая призма содержится в цилиндре. Так как при неограниченном увеличении n площади оснований призм неограниченно приближаются к площади основания цилиндра S, то их объемы неограниченно приближаются к SН. Согласно определению объем цилиндра

Итак, объем цилиндра равен произведению площади основания на высоту.

Как нарисовать лежачий цилиндр

1 этап – построение цилиндра

Сначала обозначаем ось симметрии цилиндра, которая будет находиться под наклоном. Далее обозначаем центральную часть эллипсов – переднего и заднего. При рисовании эллипса нужно учитывать, что передний эллипс больше по своему размеру, чем дальний. Так, каждый эллипс мы делим пополам, и немного смещаем эту половинку, для того, чтобы правая часть эллипса была чуть больше, чем левая. Это нужно для того, чтобы передать перспективное сокращение.

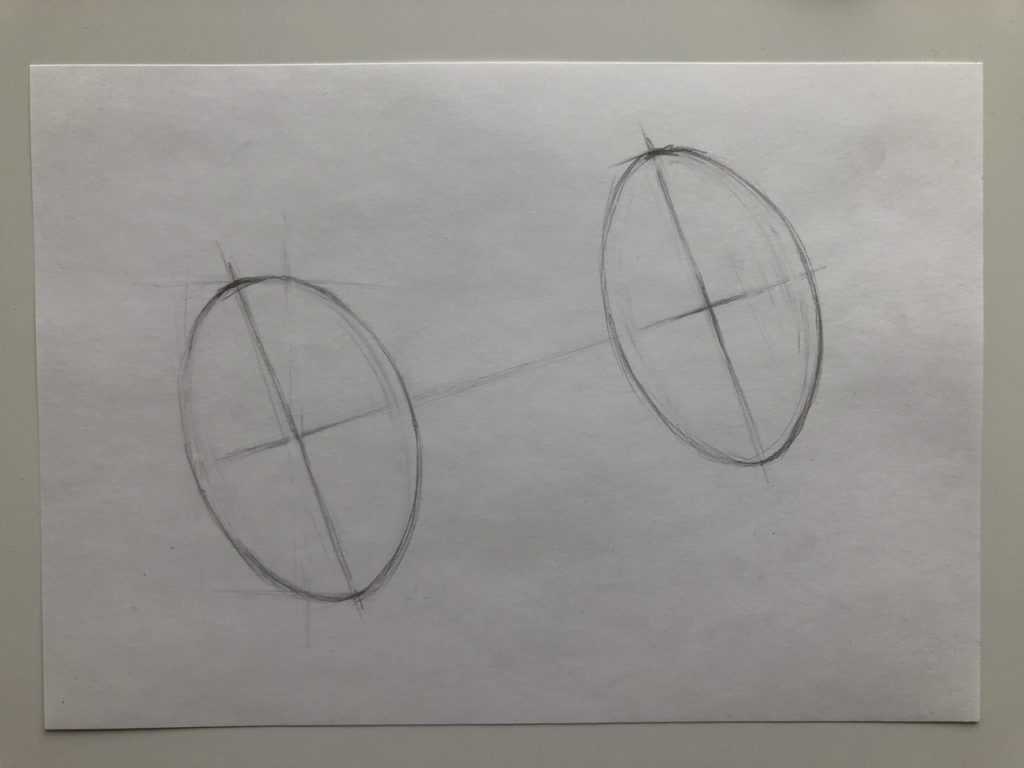
Рисуем эллипсы, стараемся их делать более закругленными и широкими, чтобы ширина эллипсов была не сильно меньше, чем высота, чтобы эллипсы не были сильно узкими, и наш цилиндр не находился в очень сильном повороте.

3 этап – уточнение формы цилиндра

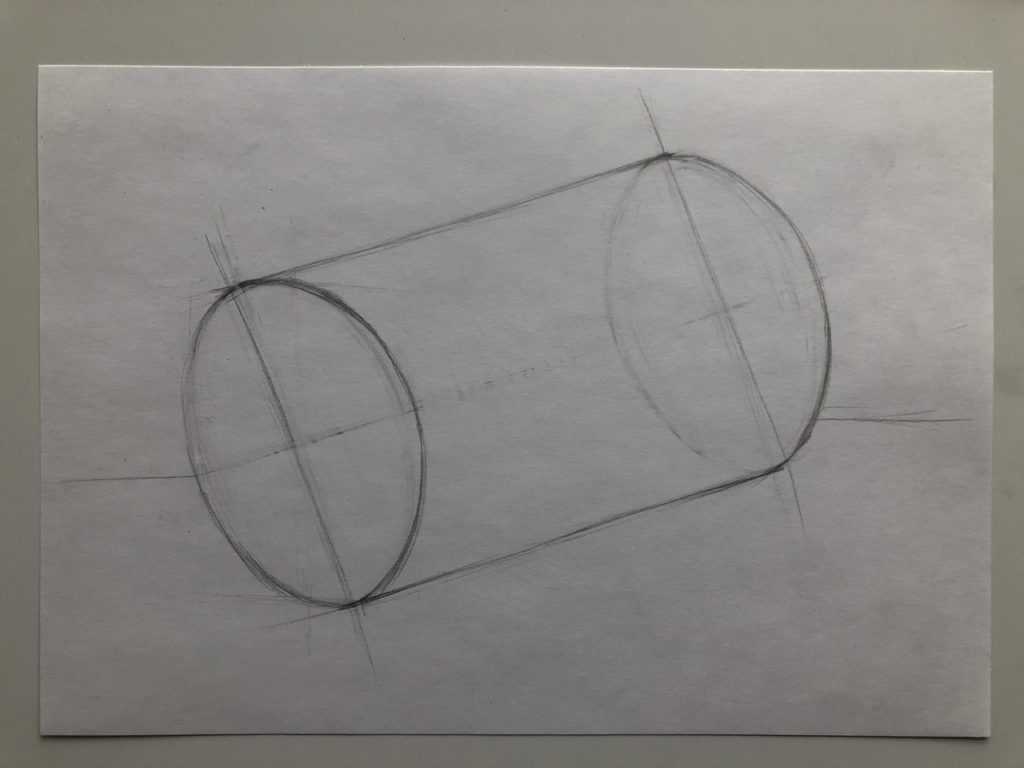
Соединяем края наших эллипсов и стираем все лишние детали ластиком. Выравниваем те части рисунка, которые у нас получились кривыми, уточняем форму нашего цилиндра.

4 этап – штриховка и наложение теней

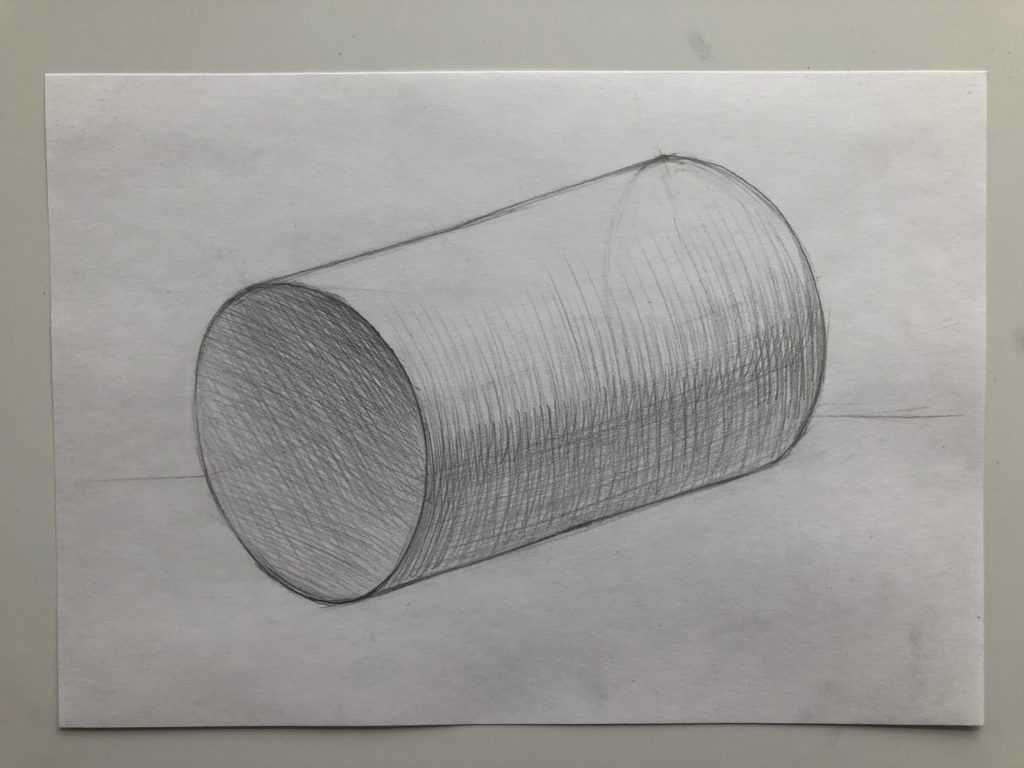
На последнем этапе, не меняя карандаш, продолжая рисовать карандашом НВ, мы начинаем штриховку цилиндра. Заштриховываем переднюю часть эллипса, сверху делая рисунок темнее, снизу чуть-чуть высветляя. Штрихи накладываем диагонально сначала в одном направлении, потом немного меняем градус – наклон нашего штриха, и немного утемняем сверху, делая легкую растяжку сверху вниз.

Далее начинаем штриховать боковую, округлую часть эллипса. Штрихуем ее полукруглыми штрихами, учитывая границы собственной тени. Эту границу мы точно также делаем полукруглыми штрихами, просто немного меняем наклон штриховки. В самом конце, можно немного диагональными штрихами по направлению цилиндра показать утемнение и границу собственной тени.

Теперь вы знаете, как сделать рисунок цилиндра простым карандашом, и сможете научиться рисовать более сложные предметы, в основе которых лежит эта геометрическая фигура.

Задача 5.

В цилиндр наклонно
вписан квадрат так, что все его вершины лежат на окружностях основания. Найдите
сторону квадрата, если высота цилиндра равна 2см, а радиус основания равен 7см.

Дано: цилиндр, h = 2см, R – 7см, АВСD − наклонно
вписанный квадрат.

В₁

D₁

А₁

Решение:

Достроим квадрат
АВСD до прямого прямоугольного параллелограмма АВС₁D₁А₁В₁СD
с диагональным сечением АВСD.

Угол АВС₁
= 90°. Так как вписанный в окружность угол, стороны которого проходят через две
данные точки окружности, равен половине угла между радиусами, проходившими в
эти точки, или дополняет половину этого угла до 180°, то АС₁ есть
диаметр окружности верхнего основания цилиндра.

Рассмотрим
прямоугольный треугольник СС₁А₁ − катет СС₁,
есть образующая цилиндра и СС₁ = 2АС, катет АС₁ есть
диаметр цилиндра и АС₁ = 14. По теореме Пифагора АС = (см).

Из прямоугольного
равнобедренного треугольника АВС по теореме Пифагора сторона квадрата АВ = см.

Ответ: АВ = 10
см.

Определение коаксиальных цилиндров

Коаксиальные цилиндры: что это такое

Коаксиальными называются цилиндры, которые находятся один внутри другого, причем их оси совпадают и образуют одну прямую линию. Такие цилиндры часто встречаются в физике, электронике и других науках, где важны электромагнитные свойства материалов.

Влияние радиуса на бесконечную длину

Радиус внутреннего цилиндра существенно влияет на бесконечную длину коаксиальных цилиндров. Бесконечной называется длина цилиндра, если он бесконечно вытягивается вдоль своей оси. Если радиус внутреннего цилиндра равен нулю, то бесконечная длина обоих цилиндров также равна нулю. Если же радиус внутреннего цилиндра стремится к бесконечности, то бесконечная длина обоих цилиндров становится бесконечной. Таким образом, радиус внутреннего цилиндра играет важную роль в свойствах коаксиальных цилиндров.

ГОСТы

Приборы внесены в Государственный Реестр измерительных приборов на основании общих требований и методов испытаний, регламентируемых Государственными стандартами и руководящими документами:

ГОСТ 29226-91 «Вискозиметры жидкостей» — основной документ;
ГОСТ 10028-81— стандарт распространяется на вискозиметры капиллярные из стекла;
ГОСТ 25271-93 — определяет условия для вискозиметров Брукфильда;
ГОСТ 6258-85 — стандарт регламентирует определение вязкости нефтепродуктов;
ГОСТ 33-2000 — методы определение кинематической вязкости и расчет динамической вязкости нефтепродуктов;
РД 50-416-83 — методические указания, регламентирующие порядок выполнения поверки стеклянных капиллярныхвискозиметров.

Слайд 13Виды цилиндра.Бесконечное тело, ограниченное замкнутой бесконечной цилиндрической поверхностью, называется бесконечным цилиндром.

Прямой круговой цилиндр — это поверхность, образованная вращением одной из параллельных прямых вокруг другой, принятой в качестве оси вращения. Бесконечное тело, ограниченное замкнутым цилиндрическим лучом и его основанием, называется открытым цилиндром. Основание и образующие цилиндрического луча называют соответственно основанием и образующими открытого цилиндра.Конечное тело, ограниченное замкнутой конечной цилиндрической поверхностью и двумя выделившими её сечениями, называется конечным цилиндром, или собственно цилиндром. Сечения называются основаниями цилиндра. По определению конечной цилиндрической поверхности, основания цилиндра равны.

Задача 10.

Найдите радиус
основания цилиндра наибольшего объема, вписанного в конус, радиус основания
которого равен 3.

Дано: конус,
цилиндр – вписан в конус, ОВ – радиус конуса, ОВ = 3.

Найти: r − радиус основания цилиндра.

Решение:

Обозначим через h
и r высоту и радиус основания цилиндра, вписанного в конус с вершиной A.
Рассмотрим осевое сечение конуса – равнобедренный треугольник ABC с высотой AO
= H и основанием BC = 2· 3 = 6 (рис.2). Плоскость ABC пересекает цилиндр,
вписанный в конус, по его осевому сечению – прямоугольнику KLMN, где точки K и
L лежат соответственно на отрезках AB и AC, а точки M и N – на отрезке BC ,
причём KL = 2r , KN = LM = h . Пусть P – точка пересечения AO и KL .
Треугольник APL подобен треугольнику AOC , поэтому

, или

откуда . Пусть V(r) – объем цилиндра, где 0 < r < 3 . Тогда

Найдем наибольшее значение функции V(r) на промежутке
(0;3) .

V'(r) =  H(2r — r2) =  Hr(2 — r).

Промежутку (0;3) принадлежит единственный корень ( r = 2 )
полученного уравнения. Если 0 < r < 2 , то V'(r) > 0 . Поэтому на
промежутке (0;2) функция V(r) возрастает. Если 2 < r < 3 , то V'(r) < 0
. Поэтому на промежутке (2;3) функция V(r) убывает. Значит, в точке r = 2 функция
V(r) имеет максимум. Следовательно, радиус основания цилиндра наибольшего объема,
вписанного в данный конус, равен 2.

Ответ: r = 2.

Виды вязкости. Как определить

Вязкость — это способность веществ сопротивляться собственному течению за счет сил молекулярного взаимодействия.

Различают два вида вязкости:

Динамическая вязкость.

Это показатель густоты в реальных условиях, при температуре окружающей среды и анализируемого вещества 18-22 °С. Показатель повышается с увеличением давления и снижается при повышении температуры жидкости. Измерения выполняются по системе СИ (Международная система единиц) в Па·с (паскаль-секунда).

Кинематическая вязкость.

Измерение проводится при определенном давлении и температуре. Показатель кинематической вязкости соответствует отношению коэффициента динамической вязкости к плотности жидкостей или газов и измеряется в Стоксах (Ст), или метрах квадратных в секунду (м2/с).

Таблица 1. Вязкость жидкостей при температуре 20°С.

Динамическая вязкость 10-3 кг/(м·с)

Кинематическая вязкость10-6кг/(м2·с-1)

Площадь поверхности цилиндра

Площадь боковой поверхности

Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.

Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой и длиной , равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:

В частности, для прямого кругового цилиндра:

, и

Для наклонного цилиндра площадь боковой поверхности равна длине образующей, умноженной на периметр сечения, перпендикулярного образующей:

Простой формулы, выражающей площадь боковой поверхности косого цилиндра через параметры основания и высоту, в отличие от объёма, к сожалению, не существует.

Виды сечений цилиндра

Осевое сечение цилиндра – прямоугольник, образованный в результате пересечения фигуры плоскостью, проходящей через ее ось. В нашем случае – это ABCD (см. первый рисунок публикации). Площадь такого сечения равна произведению высоты цилиндра на диаметр его основания.
Если секущая плоскость проходит не по оси цилиндра, но при этом перпендикулярна его основаниям, то сечением, также, является прямоугольник.
Если секущая плоскость параллельна основаниям фигуры, то сечение – это идентичный основаниям круг.
Если цилиндр пересекается плоскостью, не параллельной его основаниям и, при этом, не касающейся ни одной из них, то сечением является эллипс.
Если секущая плоскость пересекает одно из оснований цилиндра, сечением будет парабола/гипербола.

Примечания

Wikimedia Foundation . 2010 .

Смотреть что такое «Цилиндр» в других словарях:

ЦИЛИНДР — (лат. cylindrus) 1) геометрическое тело, ограниченное с концов двумя кругами, с боков плоскостью, огибающею эти круги. 2) в часовом мастерстве: особого рода рычаг двойного колеса. 3) шляпа, имеющая форму цилиндра. Словарь иностранных слов,… … Словарь иностранных слов русского языка

цилиндр — а, м. cylindre m., нем. Zylinder &LT;, лат. cylindrus &LT;гр. 1. Геометрическое тело, образуемое вращение прямоугольника вокруг одной из его сторон. Объем цилиндра. БАС 1. Толстота цилиндра равна площади его основанья, помноженной на высоту. Даль … Исторический словарь галлицизмов русского языка

ЦИЛИНДР — муж., греч. прямая стопка, вал; облец, обляк; тело, ограниченное с концов двумя кругами, а с боков гнутою по кругам плоскостью. Толстота цилиндра равна площади его основанья, помноженной на высоту, геом. Паровой цилиндр, халява, труба, в которой… … Толковый словарь Даля

цилиндр — цилиндрическая поверхность, барабан, вал; шапокляк, шляпа, ролик, рол, дорн, цилиндрик, пойнт, царга, тело, вальц Словарь русских синонимов. цилиндр сущ., кол во синонимов: 22 • атактостела (2) … Словарь синонимов

ЦИЛИНДР — (от греч. kylindros) в элементарной геометрии геометрическое тело, образованное вращением прямоугольника около одной стороны: объем цилиндра V=?r2h, а площадь боковой поверхности S = 2?rh. Боковая поверхность цилиндра есть часть цилиндрической… … Большой Энциклопедический словарь

ЦИЛИНДР — полая деталь с цилиндрической внутренней поверхностью, в которой движется поршень. Одна из основных деталей поршневых машин и механизмов … Большой Энциклопедический словарь

ЦИЛИНДР — высокая мужская шляпа из шелкового плюша с небольшими твердыми полями … Большой Энциклопедический словарь

ЦИЛИНДР — ЦИЛИНДР, твердое тело или поверхность, образуемые вращением прямоугольника вокруг одной из его сторон в качестве оси. Объем цилиндра, если обозначить его высоту как h, а радиус основания как r, равен pr2h, а площадь изогнутой поверхности 2prh … Научно-технический энциклопедический словарь

ЦИЛИНДР — ЦИЛИНДР, цилиндра, муж. (от греч. kylindros). 1. Геометрическое тело, образуемое вращением прямоугольника около одной из его сторон, называемой осью, и имеющее в основаниях круг (мат.). 2. Часть машин (двигателей, насосов, компрессоров и т.д.) в… … Толковый словарь Ушакова

ЦИЛИНДР — ЦИЛИНДР, а, муж. 1. Геометрическое тело, образованное вращением прямоугольника вокруг одной из его сторон. 2. Колонновидный предмет, напр. часть поршневой машины. 3. Высокая твёрдая шляпа такой формы с небольшими полями. Чёрный ц. | прил.… … Толковый словарь Ожегова

ЦИЛИНДР — (Steam cylinder) одна из основных деталей поршневых машин. Выполняется в виде полого круглого Ц., в котором движется поршень. Ц. паровых машин снабжается обычно паровой рубашкой для обогревания его стенок в целях уменьшения конденсации пара.… … Морской словарь

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Основные элементы цилиндра

Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

длина данного прямоугольника равна длине окружности основания цилиндра (2πR);
ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Виды цилиндров

Прямой цилиндр – имеет одинаковые симметричные основания (круг или эллипс), параллельные друг другу. Отрезок между точками симметрии оснований перпендикулярен им, является осью симметрии и высотой фигуры.
Наклонный цилиндр – имеет одинаковые симметричные и параллельные друг другу основания. Но отрезок между точками симметрии не перпендикулярен этим основаниям.
Косой (скошенный) цилиндр – основания фигуры не взаимно параллельны.
Круговой цилиндр – основаниями является круг. Также выделяют эллиптические, параболические и гиперболические цилиндры.
Равносторонний цилиндр – прямой круговой цилиндр, диаметр основания которого равен его высоте.

Развертка круглого прямого цилиндра

Когда говорят о развертке цилиндра, то подразумевают общую площадь его поверхности, представленную плоскими фигурами. Круглый прямой цилиндр образован двумя кругами, имеющими одинаковые радиусы, и одной боковой поверхностью, которая эти круги соединяет друг с другом.

На рисунке показан бумажный цилиндр. Как осуществляется построение развертки цилиндра? Возьмем воображаемые ножницы и отрежем одно основание вдоль окружности. Затем проделаем аналогичные действия со вторым основанием. Боковую поверхность разрежем вдоль генератрисы, то есть параллельно оси фигуры, и развернем ее. Таким образом, мы получили развертку, которая показана на рисунке ниже.

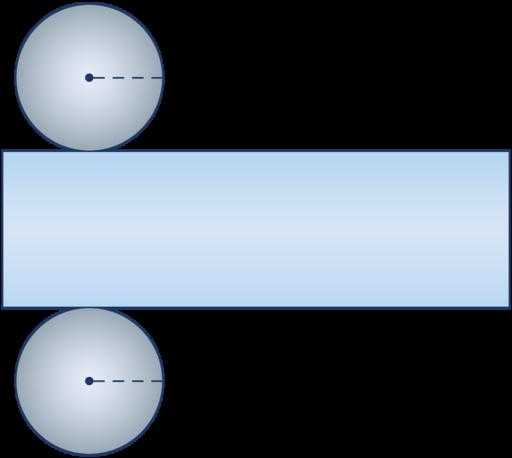
Очевидно, что она состоит из двух одинаковых кругов. Что касается цилиндрической поверхности, то в разрезанном виде она представлена прямоугольником. Развертку удобно использовать при определении площади поверхности рассматриваемой фигуры.

Слайд 49В него входят: помощь при сердечно-сосудистых заболеваниях, нейротрофических заболеваниях, гипертонии, болезнях

выводящих путей, астме, бессоннице, головных болях, а также в качестве средства для снятия стрессов и профилактике атеросклероза. Одна из удивительных особенностей Цилиндров Фараона — улучшение работы практически всех основных систем организма (показатели работы этих систем улучшаются в среднем в 2 — 2.5 раза).Согласно мнению ряда врачей, Цилиндры Фараона представляют собой уникальный, самонастраивающийся на каждого человека, физиотерапевтический прибор, созданный гением древнеегипетских ученых. Их целебные свойства, включающие в себя металлотерапию, гальванотерапию и магнитотерапию позволили врачу-биоэнергетику Т.Мешковой разработать эффективную методику использования Цилиндров. Цилиндры Фараона полезны как взрослым людям, так и детям. Они создают в организме человека обстановку, при которой ему гораздо легче справляться со своими бедами. Цилиндры — прекраснее профилактическое средство против ряда болезней. Согласно результатам экспериментов врача Т.Мешковой, Цилиндры Фараона защищают от воздействия излучений различной электронной техники: компьютеров, телевизоров, микроволновых печей и т.д.

Где используются вискозиметр

Вискозиметры используются для контроля вязкости различных веществ, участвующих в технологических процессах во многих отраслях:

в медицине приборы используются для измерения вязкости крови человека;
в фармакологии и косметологии — определение состояния лекарственных препаратов, кремов, мазей и сиропов;
в пищевой промышленности — анализ напитков, молочных продуктов, меда;
в химическом производстве — определение вязкости жидких и текучих материалов;
в строительстве — изготовление лакокрасочных материалов, шпаклевок, клеев, паст.

Постоянно приходится прибегать к регулярному анализу вязкости нефти и продуктов ее переработки в нефтяной отрасли.

Что представляют собой вискозиметры

Производится большое количество приборов для анализа вязкости, каждый из которых разработан для определенных веществ и условий измерений.

К наиболее популярным вискозиметрам относятся капиллярные и ротационные устройства:

Капиллярный прибор состоит из следующих основных частей:

емкости для измерения количества протекающей через капилляр жидкости;
полой U — образной трубки;
калиброванного капилляра, диаметром от 0,3 до 0,7 мм;
блока для определения скорости течения жидкости.

Показатель вязкости определяется по времени истеченияисследуемого вещества через капилляр заданного диаметра.

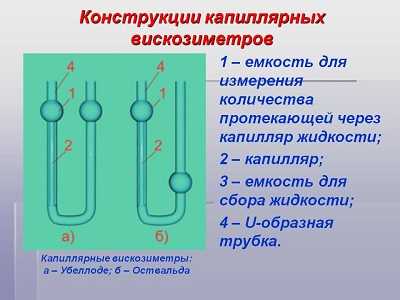
Конструкция капиллярных вискозиметров.

Основным преимуществом капиллярных измерителей вязкости является возможность моделирования реальных технологических процессов.

Основные узлы ротационных устройств:

цилиндрический резервуар, заполняемый исследуемым веществом;
внутреннийцилиндр, соосно помещаемый в полый резервуар;
электродвигатель, придающий движение ротору;
электронный блок управления с датчиками.

Один из цилиндров вращается (ротор), а другой (статор) находится в неподвижном состоянии.

Несмотря на широкий ассортимент выпускаемых вискозиметров, их разработки продолжаются, с целью повышения точности и расширения пределов измерений, обеспечения автоматического управления непрерывной работы.

Слайд 48Цилиндры Фараона — два загадочных предмета цилиндрической формы в руках некоторых

древнеегипетских изваяний. Среди специалистов-египтологов не существует единого мнения о происхождении данных предметов. В 1976 году в Закавказье Р.Добровольским и В.Ковтуном была обнаружена старинная эзотерическая рукопись под названием «Тайны Жизни и Смерти», в которой содержалась информация о Лунном и Солнечном цилиндрах, изготовленных из цинка и меди с определенным внутренним наполнением. По утверждению неизвестного автора Цилиндры Фараона использовались фараонами и жрецами Древнего Египта для укрепления жизненных сил и общения с богами. Цилиндры Фараона были воссозданы согласно древнему рецепту и затем в течение многих лет исследовались физиком Владимиром Ковтуном. В этих исследованиях принимали участие медики, физики, египтологи, экстрасенсы и парапсихологи. Результаты исследований поразили ученых. Оказалось, что Цилиндры Фараона обладают широчайшим спектром благотворного воздействия на организм человека.

1.1. Определение цилиндра

Рассмотрим
какую-либо линию (кривую, ломаную или смешанную) l, лежащую в некоторой
плокости α, и некоторую прямую S, пересекающую эту плоскость. Через все
точки данной линии l проведем прямые, параллельные прямой S; образованная этими
прямыми поверхность α называется цилиндрической поверхностью. Линия l
называется направляющей этой поверхности, прямые s1, s2,
s3,… − ее образующими.

Если направляющая
является ломаной, то такая цилиндрическая поверхность состоит из ряда плоских
полос, заключенных между парами параллельных прямых, и называется
призматической поверхностью. Образующие, проходящие через вершины направляющей
ломаной, называются ребрами призматической поверхности, плоские полосы между ними
− ее гранями.

Если рассечь
любую цилиндрическую поверхность произвольной плоскостью, не параллельной ее
образующим, то получим линию, которая также может быть принята за направляющую
данной поверхности. Среди направляющих выделяется та, которая, получается, от
сечения поверхности плоскостью, перпендикулярной образующим поверхности. Такое
сечение называется нормальным сечением, а соответствующая направляющая −
нормальной направляющей.

Если направляющая
− замкнутая (выпуклая) линия (ломаная или кривая), то соответствующая
поверхность называется замкнутой (выпуклой) призматической или цилиндрической
поверхностью. Из цилиндрических поверхностей простейшая имеет своей нормальной
направляющей окружность. Рассечем замкнутую выпуклую призматическую поверхность
двумя плоскостями, параллельными между собой, но не параллельными образующим.

В сечениях
получим выпуклые многоугольники. Теперь часть призматической поверхности,
заключенная между плоскостями α и α’, и две образовавшиеся при этом
многоугольные пластинки в этих плоскостях ограничивают тело, называемое
призматическим телом − призмой.

Цилиндрическое
тело − цилиндр определяется аналогично призме:
Цилиндром называется тело, ограниченное с боков замкнутой (выпуклой)
цилиндрической поверхностью, а с торцов двумя плоскими параллельными
основаниями. Оба основания цилиндра равны, также равны между собой и все
образующие цилиндра, т.е. отрезки образующих цилиндрической поверхности между
плоскостями оснований.

Цилиндром
(точнее, круговым цилиндром) называется геометрическое тело, которое состоит
из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным
переносом, и всех отрезков, соединяющих соответствующие точки этих кругов (рис.
1).

Рис. 1 −
Цилиндр

Круги называются
основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей
кругов, − образующими цилиндра.

Так как
параллельный перенос есть движение, то основания цилиндра равны.

Так как при
параллельном переносе плоскость переходит в параллельную плоскость (или в
себя), то у цилиндра основания лежат в параллельных плоскостях.

Так как при
параллельном переносе точки смещаются по параллельным (или совпадающим) прямым
на одно и то же расстояние, то у цилиндра образующие параллельны и равны.

Поверхность
цилиндра состоит из оснований и боковой поверхности. Боковая поверхность
составлена из образующих.

Цилиндр называется
прямым, если его образующие перпендикулярны плоскостям оснований.

Прямой цилиндр
наглядно можно представить себе как геометрическое тело, которое описывает
прямоугольник при вращении его около стороны как оси (рис. 2).

Рис. 2 −
Прямой цилиндр

В дальнейшем мы
будем рассматривать только прямой цилиндр, называя его для краткости просто
цилиндром.

Радиусом цилиндра
называется радиус его основания. Высотой цилиндра называется расстояние между
плоскостями его оснований. Осью цилиндра называется прямая, проходящая через
центры оснований. Она параллельна образующим.

Цилиндр
называется равносторонним, если
его высота равна диаметру основания.

Если основания
цилиндра плоские (и, следовательно, содержащие их плоскости параллельны), то
цилиндр называют стоящим на плоскости. Если основания стоящего на плоскости
цилиндра перпендикулярны образующей, то цилиндр называется прямым.

В частности, если
основание стоящего на плоскости цилиндра − круг, то говорят о круговом (круглом)
цилиндре; если эллипс − то эллиптическом.