Лекция 7. поверхности

Объём цилиндра

Для наклонного цилиндра существуют две формулы:

• Объём равен длине образующей, умноженной на площадь сечения цилиндра плоскостью, перпендикулярной образующей.

  \displaystyle{ V=S_{\perp}l },

• Объём равен площади основания, умноженной на высоту (расстояние между плоскостями, в которых лежат основания):

  \displaystyle{ V=Sh=Sl\sin{\varphi} },

где \displaystyle{ l } — длина образующей, а \displaystyle{ \varphi } — угол между образующей и плоскостью основания. Для прямого цилиндра \displaystyle{ h=l }.

Для прямого цилиндра \displaystyle{ \sin{\varphi}=1 }, \displaystyle{ l=h } и \displaystyle{ S_{\perp}=S }, и объём равен:

\displaystyle{ V=Sl=Sh }

Для кругового цилиндра:

\displaystyle{ V=\pi R^{2}h=\pi \frac{d^{2}}{4}h },

где d — диаметр основания.

Цилиндр как фигура геометрии

Предположим, что у нас имеется некоторая плавная кривая. Это может быть круг, эллипс, парабола и так далее. Возьмем отрезок произвольной длины, который не лежит в плоскости кривой, и опишем с помощью него поверхность, следуя направлению кривой и транслируя отрезок параллельно самому себе. Полученная поверхность называется цилиндрической или просто цилиндром. Отмеченная кривая называется директрисой (направляющей), а отрезок — генератрисой (образующей).

Если к цилиндрической поверхности добавить еще две плоские одинаковые фигуры, ограничивающие эту поверхность с торцов, то полученное тело также называется цилиндром. Оно состоит из двух равных оснований и цилиндрической поверхности.

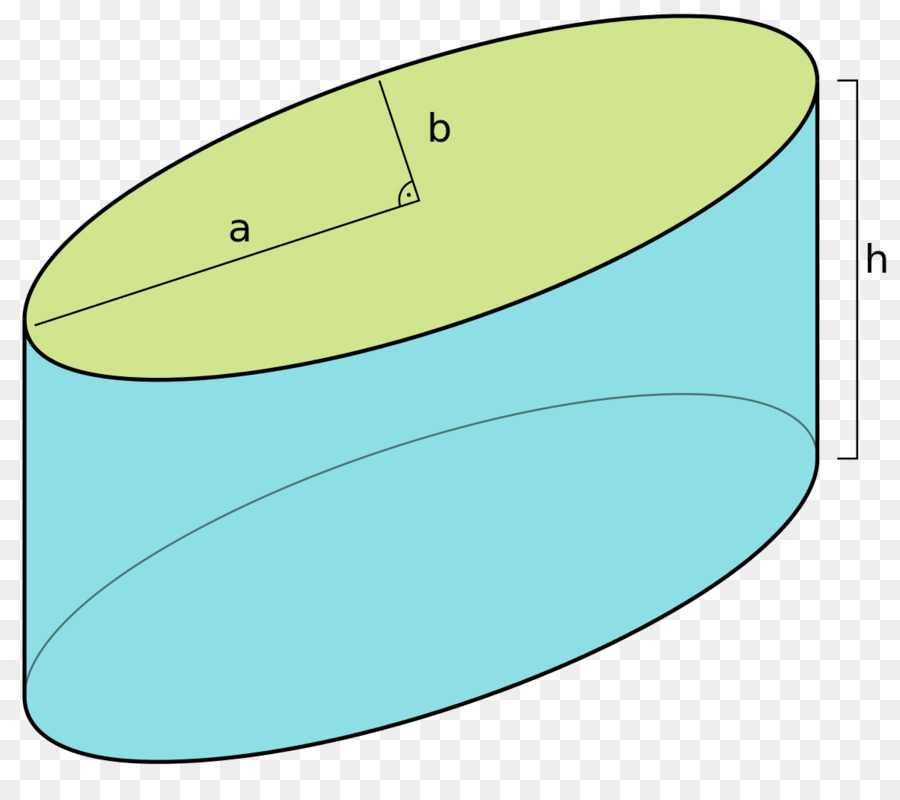
Для наглядного представления описанной фигуры ниже приведен рисунок. На нем изображен эллиптический цилиндр, имеющий полуоси a и b и высоту h (дистанция между основаниями).

Упражнение

Заданы: сфера и  прямая общего положения АВ.

Найти: точки пересечения прямой с поверхностью сферы (точки «входа» и «выхода»).

Чтобы найти точки пересечения прямой с поверхностью сферы необходимо:

1. Заключить прямую во вспомогательную плоскость, пересекающую поверхность сферы так, чтобы получались простые фигуры (например, круг, ограниченный окружностью);
2. Построить фигуру пересечения сферы вспомогательной плоскостью;
3. Найти общие точки прямой и контура фигуры (окружность): так как прямая и окружность лежат в одной плоскости, то они, пересекаясь, образуют точки, общие для прямой и сферы, которые и будут являться искомыми точками (Рисунок 7.12).

Решение

Через прямую проводим плоскость σ. Пусть σ⊥π1 и пересекает сферу по окружности радиусом r. С – центр окружности сечения ОС⊥σ:

Рисунок 7.12 – Пересечение прямой с поверхностью сферы

• Введём π₃⊥π₁ и π₃//σ₁. Построим проекцию окружности сечения на π₃ и проекцию А₃В₃.
• Находим точки их пересечения 1₂ и 2₃.
• Определим видимость участков прямой.
• На π₁ точки 1 и 2 находятся на переднем полушарии, следовательно, на π₂ они видимы.

3. Сечения цилиндра

Сечение цилиндра
плоскостью, параллельной его оси, представляет собой прямоугольник (рис. 3, а).
Две его стороны − образующие цилиндра, а две другие − параллельные
хорды оснований.

а)                б)

    в)                   г) 

Рис. 3 – Сечения
цилиндра

В частности,
прямоугольником является осевое сечение. Это − сечение  цилиндра
плоскостью, проходящей через его ось (рис. 3, б).

 Сечение цилиндра
плоскостью, параллельной основанию − круг (рис 3,  в).

Сечение цилиндра
плоскостью не параллельной основанию и его оси − овал  (рис. 3г).

Доказательство.
Пусть β − плоскость, параллельная плоскости основания цилиндра.
Параллельный перенос в направлении оси цилиндра, совмещающий плоскость β с
плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью
β с окружностью основания. Теорема доказана.  

Площадь
боковой поверхности цилиндра.

За площадь боковой
поверхности цилиндра принимается предел, к которому стремится площадь боковой
поверхности правильной призмы, вписанной в цилиндр, когда число сторон
основания этой призмы неограниченно возрастет.

Теорема 2.
Площадь боковой поверхности цилиндра равна произведению длины окружности его
основания на высоту (S_бок.ц = 2πRH, где R − радиус
основания цилиндра, Н − высота цилиндра).

а)          б)   
Рис. 4 − Площадь
боковой поверхности цилиндра

 Доказательство.

Пусть P_nи Н соответственно периметр основания
и высота правильной n-угольной призмы, вписанной в цилиндр (рис. 4, а). Тогда
площадь боковой поверхности этой призмы S_бок.ц − P_nH. Предположим, что число сторон
многоугольника, вписанного в основание, неограниченно растет (рис. 4, б). Тогда
периметр P_n стремится к длине окружности С = 2πR,
где R— радиус основания цилиндра, а высота H не изменяется. Таким образом,
площадь боковой поверхности призмы стремится к пределу 2πRH,
т. е. площадь боковой
поверхности цилиндра равна S_бок.ц = 2πRH.
Теорема доказана.

Площадь полной
поверхности цилиндра.

Площадью полной
поверхности цилиндра называется сумма площадей боковой поверхности и двух
оснований. Площадь каждого основания цилиндра равна πR2,
следовательно, площадь полной   поверхности  
цилиндра  S_полн вычисляется  
по   формуле S_бок.ц = 2πRH+ 2πR2.

r

T1

T

F

F1

F

T

F

Рис. 5 − Площадь
полной поверхности цилиндра

Если боковую
поверхность цилиндра разрезать по образующей FT (рис. 5, а) и развернуть так,
чтобы все образующие оказались в одной плоскости, то в результате мы получим
прямоугольник FTT1F1, который называется разверткой боковой поверхности
цилиндра. Сторона FF1 прямоугольника есть развертка окружности основания
цилиндра, следовательно, FF1=2πR, а его сторона FT равна образующей
цилиндра, т. е. FT = Н (рис. 5, б). Таким образом, площадь FT∙FF1=2πRH
развертки цилиндра равна пло­щади его боковой поверхности.

Типы цилиндров[править | править код]

• Прямым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), прямая между которыми перпендикулярна плоскостям этих оснований. Данная прямая называется осью цилиндра.
• Косым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), отрезок между которыми не перпендикулярен плоскостям этих оснований.
• Круговым называется цилиндр с окружностью в роли направляющей.
• Цилиндром вращения, или прямым круговым цилиндром (часто под цилиндром подразумевают именно его) называется цилиндр, который можно получить вращением (то есть тело вращения) прямоугольника вокруг одной из его сторон, содержащая которую прямая в таком случае будет осью этого цилиндра и его осью симметрии.
• Цилиндр, основания которого являются эллипсами, параболами или гиперболами, называют соответственно эллиптическим, параболическим и гиперболическим; последние два имеют бесконечный объём.
• Призма также является разновидностью цилиндра — с основанием в виде многоугольника.
• Равносторонним называется цилиндр вращения, диаметр основания которого равен его высоте.

Сечения (сечение плоскостью)

Результат пересечения цилиндров

Понятие отверстия в кольце

Отверстие в кольце – это пространство внутри кольца, которое не заполнено материалом и образует внутреннюю полость кольца. По форме отверстие может быть круглым, овальным, квадратным или любой другой формы, в зависимости от размеров и конструкции кольца.

Правильное определение отверстия в кольце имеет значение для правильной выборки украшения. Кольца с отверстием могут быть названы полыми кольцами или донутами, хотя каждый из этих терминов имеет некоторые отличия. Донуты имеют более широкое отверстие, чем полые кольца, и они обычно используются для соединения нескольких колец или для создания больших украшений.

Независимо от того, как называется круг с отверстием, отверстие является важным элементом дизайна, который добавляет украшению уникальность и индивидуальность.

7.10. Пересечение цилиндра плоскостью

Пусть плоскость сечения γ – фронтально-проецирующая (Рисунок 7.15).

1. Если плоскость сечения γ параллельна оси цилиндра, то она пересекает цилиндр по четырехугольнику.
2. Если плоскость сечения γ перпендикулярна оси цилиндра, то она пересекает цилиндр по окружности.
3. Если плоскость сечения γ не параллельна и не перпендикулярна оси цилиндра в сечении эллипс.

Рассмотрим алгоритм построения сечения – эллипс (Рисунок 7.15):

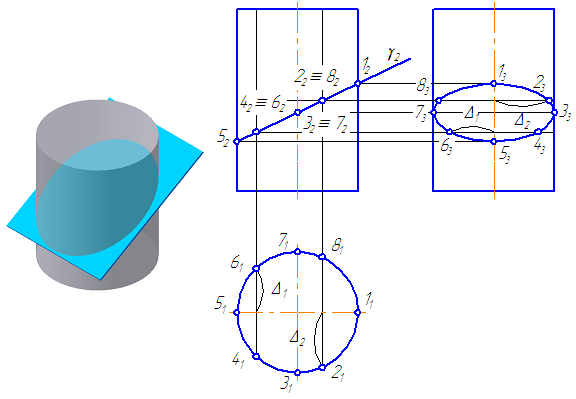
Рисунок 7.15 – пересечение цилиндра плоскостью

1. Находим и строим характерные точки (точки, не требующие дополнительных построений) – в нашем случае, точки принадлежащие крайним образующим – 1, 3, 5, 7. Одновременно с этим, данные точки определяют величину большой и малой оси эллипса.
2. Для построения участка эллипса необходимо построить не менее 5-ти точек (так как лекальная кривая второго порядка определяется как минимум пятью точками). Для построения точек 2, 4, 6, 8 возьмем на π₁ произвольно расположенные образующие цилиндра, которые проецируются на данную плоскость проекции в точки.
3. Построим вторые проекции данных образующих. Из точек пересечения вторых проекций образующих с проекцией плоскости сечения γ проводим линии связи к π₃. Для построения третьей проекции, например, точки 6 измеряем расстояние Δ₁ и откладываем его по соответствующей линии связи на π₃. Симметрично ей, относительно оси вращения, строим точку 4. Аналогично строятся другие точки.

Типы цилиндров

• Прямым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), прямая между которыми перпендикулярна плоскостям этих оснований. Данная прямая называется осью цилиндра.
• Косым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), отрезок между которыми не перпендикулярен плоскостям этих оснований.
• Круговым называется цилиндр с окружностью в роли направляющей.
• Цилиндром вращения, или прямым круговым цилиндром (часто под цилиндром подразумевают именно его) называется цилиндр, который можно получить вращением (то есть тело вращения) прямоугольника вокруг одной из его сторон, содержащая которую прямая в таком случае будет осью этого цилиндра и его осью симметрии.
• Цилиндр, основания которого являются эллипсами, параболами или гиперболами, называют соответственно эллиптическим, параболическим и гиперболическим; последние два имеют бесконечный объём.
• Призма также является разновидностью цилиндра — с основанием в виде многоугольника.
• Равносторонним называется цилиндр вращения, диаметр основания которого равен его высоте.

Сечения (сечение плоскостью)

Результат пересечения цилиндров

Площадь поверхности цилиндра

Площадь боковой поверхности

К вычислению площади боковой поверхности цилиндра

Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.

Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой \displaystyle{ h } и длиной \displaystyle{ P }, равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:

\displaystyle{ S_b = P h }

В частности, для прямого кругового цилиндра:

\displaystyle{ P = 2 \pi R }, и \displaystyle{ S_b = 2 \pi R h }, здесь и далее \displaystyle{ R } — радиус основания цилиндра.

Для наклонного цилиндра площадь боковой поверхности равна длине образующей, умноженной на периметр сечения, перпендикулярного образующей:

\displaystyle{ S_b = P_{\perp} h }

Простой формулы, выражающей площадь боковой поверхности косого цилиндра через параметры основания и высоту, в отличие от объёма не существует. Для наклонного кругового цилиндра можно воспользоваться , а затем умножить полученное значение на длину образующей.

Площадь полной поверхности

Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.

Для прямого кругового цилиндра:
\displaystyle{ S_{p} = 2 \pi R h +2 \pi R^2 = 2\pi R (h+R) }

Слайд 42Винтовые линии бывают правовинтовые и левовинтовые.Предположим, что по винтовой линии движется

точка. Проекцией винтовой линии на плоскость, перпендикулярную кеё оси (будем называть осью винтовой линии ось цилиндра, на котором она расположена), будет, очевидно, окружность. Поэтому если смотреть на винтовую линию в направлении её оси, то будет казаться, что точка движется по окружности. Если точка движется по окружности по часовой стрелке, удаляясь от нас, то винтовая линия называется право- винтовой, если же она движется по часовой стрелке, приближаясь к нам, то винтовая линия называется левовин- товой. Правовинтовую и левовинтовую линии на одном итом же цилиндре с одинаковым углом подъёма совместить нельзя. На черт.1 у нас получилась левовинтовая линия; чтобы получить правовинтовую линию, нужно наматывать треугольник в противоположном направлении.

Типы цилиндров[править | править код]

• Прямым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), прямая между которыми перпендикулярна плоскостям этих оснований. Данная прямая называется осью цилиндра.
• Косым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), отрезок между которыми не перпендикулярен плоскостям этих оснований.
• Круговым называется цилиндр с окружностью в роли направляющей.
• Цилиндром вращения, или прямым круговым цилиндром (часто под цилиндром подразумевают именно его) называется цилиндр, который можно получить вращением (то есть тело вращения) прямоугольника вокруг одной из его сторон, содержащая которую прямая в таком случае будет осью этого цилиндра и его осью симметрии.
• Цилиндр, основания которого являются эллипсами, параболами или гиперболами, называют соответственно эллиптическим, параболическим и гиперболическим; последние два имеют бесконечный объём.
• Призма также является разновидностью цилиндра — с основанием в виде многоугольника.
• Равносторонним называется цилиндр вращения, диаметр основания которого равен его высоте.

Цилиндр

Цили́ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями, это основания цилиндра. Таким образом, граница основания будет по форме совпадать с направляющей.

В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность и основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.

Другие виды цилиндра — (по наклону образующей) косой или наклонный (если образующая касается основания не под прямым углом); (по форме основания) эллиптический, гиперболический, параболический.

Призма также является разновидностью цилиндра — с основанием в виде многоугольника.

Слайд 6Вклад Кавальери в математику.

В своем основном труде «Геометрия» (1635г.) Кавальери развил разработанный им задолго до выхода книги новый метод определения площадей и объемов – так называемый метод неделимых. Неделимыми Кавальери называл параллельные между собой хорды плоской фигуры или параллельные плоскости тела. Важнейший признак неделимости состоит в том, что число измерений его на единицу меньше самого геометрического образа. У плоской фигуры 2 измерения, у ее неделимого, т.е. у отрезка – 1 измерение. Кавальери доказал теорему о том, что площади двух подобных фигур относятся как квадраты, а объемы – как кубы соответствующих неделимых, и установил, что отношение суммы квадратов всех неделимых треугольника к сумме квадратов всех неделимых параллелограмма, имеющего с треугольником одинаковые основания и высоту, равно 1:3. Впоследствии Кавальери нашел аналогичные соотношения для суммы кубов и т.д. до девятой степени неделимых. Труды Кавальери сыграли огромную роль в формировании исчисления бесконечно малых.

Слайд 53С примерами винтовой линии мы часто встречаемся в физике и технике.

Форму винтовой линии с очень малым углом имеет каждый слой проволоки в индукционной катушке. При равномерной подаче резец токарного станка при обточке цилиндра оставляет на этом цилиндре след в виде винтовой линии. Форму винтовой линии имеет режущая кромка цилиндрических спиральных свёрл. Форма нарезки на всякого рода скрепляющих, регулировочных винтах, болтах и гайках — винтовая линия (причём, как правило, применяется правовинтовая нарезка). При прямолинейном равномерном полёте точка на пропеллере самолёта описывает винтовую линию. Точно так же винтовую линию описывает точка на гребном винте как океанского парохода, так и моторной лодки. Форму винтовой линии имеет штопор, употребляемый для раскупоривания бутылок. Винтовую линию описывает точка крыла самолёта, когда он «входит в штопор». При прямолинейном равномерном полёте винтовочной пули, а также артиллерийского снаряда точки на их поверхности описывают винтовые линии. Во всех перечисленных примерах научно-технического характера при производимых расчётах используются те или иные свойства винтовой линии. Число и характер приведённых примеров говорят о важных практических применениях винтовой линии.

Как называется круг с лункой: полое кольцо или донут?

Слово «донут» в нашей речи появилось сравнительно недавно и обозначает то же, что и слово «полое кольцо». Однако, донутом чаще называют кольцо с более широкой лункой, которая чаще всего бывает глубже и заметнее, чем у полого кольца.

Донут, в свою очередь, может иметь различную форму, толщину и глубину лунки, причем может состоять не только из круглого отверстия, но и из других геометрических фигур. Использование слова «донут» может быть более удобным в тех случаях, когда необходимо описать кольцо с более сложной формой лунки.

Итак, можно сказать, что полое кольцо и донут — это два синонима, в зависимости от предпочтений использующего термин.

Слайд 5Вклад Евклида в математику.О Евклиде почти ничего неизвестно, откуда он был

родом, где и у кого учился.Папп Александрийский (III в.) сообщает, что он был очень доброжелателен ко всем тем, кто сделал хоть какой-нибудь вклад в математику, корректен, в высшей степени порядочен и совершенно лишен тщеславия. Евклид, как и другие великие греческие геометры, занимался астрономией, оптикой и теорией музыки. До нас дошли его сочинения, посвященные прикладным вопросам: «Феномены» (элементарная сферическая астрономия), «Оптика» (учение о перспективе) и «Сечение канона» ( теория музыки). Это были первые прообразы будущих исследований по математической физике: в них теория выводилась строго дедуктивно из явно сформулированных физических гипотез и математических постулатов. Гораздо больше мы знаем о математическом творчестве Евклида. Прежде всего Евклид является для нас автором «Начал», по которым учились математики всего мира. Эта удивительная книга пережила более двух тысячелетии, но до сих пор не утратила своего значения не только в истории науки, но и самой математике. Созданная там система евклидовой геометрии и теперь изучается во всех школах мира и лежит в основе почти всей практической деятельности людей. На геометрии Евклида базируется классическая механика, ее апофеозом было появление в 1687 г. Математических начал натуральной философии Ньютона, где законы земной и небесной механики и физики устанавливаются в абсолютном евклидовом пространстве. Содержание «Начал» далеко не исчерпывается элементарной геометрией — это основы всей античной математики. Здесь подводится итог более чем 300-летнему ее развитию и вместе с тем создается прочная 6aзa для дальнейших исследований. Последующие математики ссылались на предложения «Начал», как на нечто окончательно установленное.

Цилиндр

Стереометрия −
это раздел геометрии, в котором изучаются фигуры в пространстве. Основными
фигурами в пространстве являются точка, прямая и плоскость. В стереометрии
появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это
одно из немногих существенных отличий стереометрии от планиметрии, так как во
многих случаях задачи по стереометрии решаются путем рассмотрения различных
плоскостей, в которых выполняются планиметрические законы.

В окружающей нас
природе существует множество объектов, являющихся физическими моделями
указанной фигуры. Например, многие детали машин имеют форму цилиндра или
представляют собой некоторое их сочетание, а величественные колонны храмов и
соборов, выполненные в форме цилиндров, подчеркивают их гармонию и красоту.

Греч. −
кюлиндрос. Античный термин. В обиходе − свиток папируса, валик, каток
(глагол − крутить, катать).

У Евклида цилиндр
получается вращением прямоугольника. У Кавальери − движением образующей
(при произвольной направляющей − «цилиндрика»).

Цель данного
реферата рассмотреть геометрическое тело – цилиндр.

Для достижения
данной цели необходимо рассмотреть следующие задачи:

− дать
определения цилиндра;

−
рассмотреть элементы цилиндра;

− изучить
свойства цилиндра;

−
рассмотреть виды сечения цилиндра;

− вывести
формулу площади цилиндра;

− вывести
формулу объема цилиндра;

− решить
задачи с использованием цилиндра.

Объём цилиндра[править | править код]

Для наклонного цилиндра существуют две формулы:

• Объём равен длине образующей, умноженной на площадь сечения цилиндра плоскостью, перпендикулярной образующей.

  V=S⊥l{\displaystyle V=S_{\perp }l},

• Объём равен площади основания, умноженной на высоту (расстояние между плоскостями, в которых лежат основания):

  V=Sh=Slsin⁡φ{\displaystyle V=Sh=Sl\sin {\varphi }},

где l{\displaystyle l} — длина образующей, а φ{\displaystyle \varphi } — угол между образующей и плоскостью основания. Для прямого цилиндра h=l{\displaystyle h=l}.

Для прямого цилиндра sin⁡φ=1{\displaystyle \sin {\varphi }=1}, l=h{\displaystyle l=h} и S⊥=S{\displaystyle S_{\perp }=S}, и объём равен:

V=Sl=Sh{\displaystyle V=Sl=Sh}

Для кругового цилиндра:

V=πR2h=πd24h{\displaystyle V=\pi R^{2}h=\pi {\frac {d^{2}}{4}}h},

где d — диаметр основания.

Применение полого цилиндра

Полый цилиндр находит широкое применение в различных отраслях промышленности и науки.

• Машиностроение: полые цилиндры используются для передачи механической энергии, например, в первичной стадии производства бумаги.
• Электроэнергетика: полый цилиндр может быть использован как обмотка для высоких напряжений в электрогенераторах.
• Нефтяная промышленность: часто используются полые цилиндры для хранения и транспортировки жидкостей, газов и продуктов нефтепереработки.
• Медицина: полые цилиндры могут использоваться в качестве имплантатов для поддержания функции тканей или органов в организме.
• Наука: полые цилиндры могут использоваться в качестве колонок для хроматографии, в лабораторных опытах для разделения и анализа химических соединений.

Благодаря своим уникальным свойствам, полые цилиндры нашли применение в разных областях и играют важную роль в современной промышленности.

Виды цилиндров

Самый простой и распространённый вид цилиндра – круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.

Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.

По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр – наклонный.

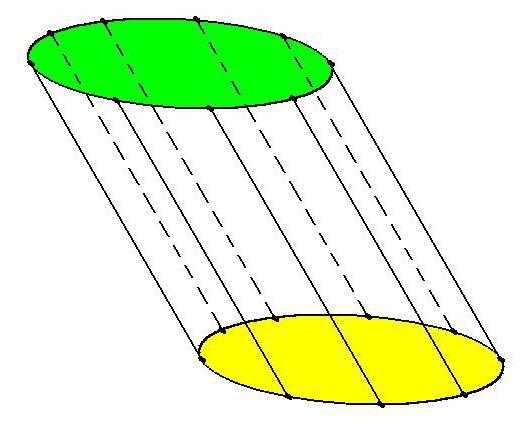
Виды цилиндров

1. Прямой цилиндр – имеет одинаковые симметричные основания (круг или эллипс), параллельные друг другу. Отрезок между точками симметрии оснований перпендикулярен им, является осью симметрии и высотой фигуры.
2. Наклонный цилиндр – имеет одинаковые симметричные и параллельные друг другу основания. Но отрезок между точками симметрии не перпендикулярен этим основаниям.
3. Косой (скошенный) цилиндр – основания фигуры не взаимно параллельны.
4. Круговой цилиндр – основаниями является круг. Также выделяют эллиптические, параболические и гиперболические цилиндры.
5. Равносторонний цилиндр – прямой круговой цилиндр, диаметр основания которого равен его высоте.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Основные элементы цилиндра

• Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
• R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
• O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
• l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

• длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
• ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;

План-конспект урока

Образовательные цели: сформировать у учащихся представления о цилиндре и связанных с ним понятий. Научить применять формулы для нахождения объема, площадей боковой и полной поверхностей цилиндра при решении задач.

Развивающие цели: содействовать развитию пространственного мышления. Содействовать развитию умений обобщать и систематизировать полученные знания.

Воспитательные цели: привить интерес к геометрии. Воспитать ответственное отношение к учебному труду.

Тип урока: урок объяснения нового материала.

1. Организационный момент.

─ проверка готовности учащихся к уроку;

─ организация внимания учащихся.

2. Объяснение нового материала.

Итак, рассмотрим понятие цилиндра. Цилиндр — это один из видов тел вращения. Вокруг нас существует множество предметов, имеющих форму цилиндра.

Далее назовем элементы цилиндра и дадим его определение:

Затем, пользуясь принципом Кавальери, докажем, объем цилиндра равен произведению площади основания на высоту.

Потом рассмотрим цилиндр с радиусом r и высотой h. Покажем его развертку и выведем формулы для вычисления площадей боковой и полной поверхностей цилиндра.

3. Обобщение и закрепление нового материала.

На этом уроке мы познакомились с понятием цилиндра. Узнали, что цилиндр — это тело, ограниченное двумя равными кругами и цилиндрической поверхностью. Рассмотрели, какими элементами он обладает. А также разобрались, как находят объем, площадь боковой поверхности и площадь полной поверхности цилиндра.

Кроме этого решили задачи на применение формул.

4. Рефлексия.

Хотелось бы узнать, понравился ли вам урок? Что было не понятным на уроке? Что еще бы вы хотели узнать?